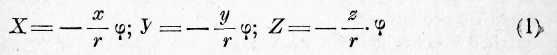
Веб-мастер приносит свои извинения за низкое качество вычитки текста после
OCR-сканированияII. Принцип сохранения силы (энергии)
Мы дадим вышеуказанному закону для случая действия центральных сил еще более общее выражение.
Пусть (о величина силы, которая действует по направлению гг считается положительной, если имеется притяжение, и отрицательной, если наблюдается отталкивание, таким образом
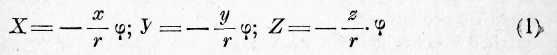
Согласно уравнению 2 предыдущего параграфа,
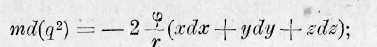
отсюда
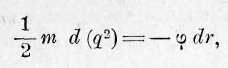
или если Q и q, R и r суть соответствующие тангенциальные скорости и расстояния, то
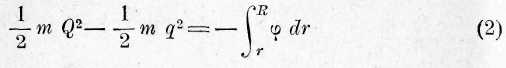
Если рассматривать ближе это уравнение, то мы найдем в левой части разность живых сил, которая соответствует разным расстояниям т от а. Чтобы найти значение величины
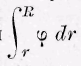
представим себе, что величины ф, которые относятся к различным точггвм линии соединяющей т и а, представлены перпендикулярно восстановленными к соответствующим точкам ординатами: указанная величина должна была бы представлять величину площади, которая заключается между кривой, ординатами соответствующими И и г и осью абсцисс. Поскольку эту площадь можно представить, как сумму бесконечного числа бесконечно малых прямоугольников
1), то эта величина есть сумма всех элементарных работ2), которые произведены на расстояниях, лежащих между Е и г. Если назвать энергию, обладая которой точка т может двигаться, но пока еще не движется, потенциальной энергией 3), в противоположность тому, что механика называетживой силой, то мы могли бы назвать величину т аг суммою потенциальных энергий
4) между расстояниями Л и г, и предыдущий закон мог бы быть выражен так: увеличение живой силы равно сумме соответствующих изменению ее расстояния потенциальных энергий1).Представим себе, что две точки, находящиеся под действием притягательной силы на определенном расстоянии Л, переводятся под влиянием воздействия силы на более близкое расстояние г, при этом их скорость, их живая сила увеличиваются; если они должны бы были перейти на более далекое расстояние г, то их живая сила югмна. была бы убывать и, наконец, должна сделаться равной нулю
2). Мы можем поэтому при притягивающих силах сумму
работ сил между пределамиобозначить как еще существующую, сумму тех же величин между г = Л и г = оо назвать, как использованную; первые могут перейти в действие непосредственно, последние только после эквивалентной потери в живой силе. Обратное наблюдается при отталкивающих силах. Если точки находятся на расстоянии Л, то при их удалении мы будем получать живую силу, и мы должны считать работой силы имеющейся в нашем распоряжении величины между г = В и г = оо, работой затраченной-величины работы между г = 0 и г = 11.
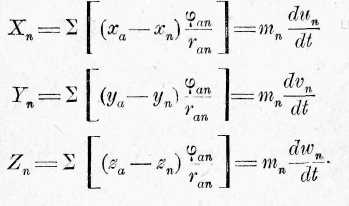
Чтобы вывести наш закон в самом общем виде, мы представим себе любое количество материальных точек, имеющих массы тл, т
2, т3, и т. д.. при чем в общем случае массу, имеющую координаты Х; У мы обозначим через та. Параллельные осям координат слагающие действующих на массу скл пусть будут Ха, Уа, Za, разложенные по осям координат скорости пусть будут ма, уа, гоа, тангенциальные скорости qa; расстояние между та и ть пусть равно центральная сила, действующая между этими двумя точками, пусть равна <сцЬ. Для одной точки пгп аналогично уравнению 1, находится :где знак суммы 2 относится ко всем членам, которые получаютс} если вместо показателя а вставить все числа 1, 2, 3... и т. д., а исключением п.
Умножим первое уравнение на
dxn = undt, второе на dyn=^vnd третье на йгп = wndt; представим себе, что три полученных такв образом уравнения написаны для всех отдельных точек тъ, как si было сделано для тп, и что эти все уравнения сложены, тог; мы получаем: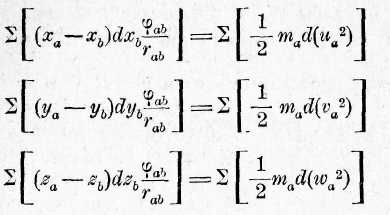
Члены рядов, находящихся в левой части равенства, будут получен если вместо а поставить отдельные индексы 1, 2,3. ..и т. д., и п каждом из них поставить для Ъ все большие и все меньшие вел чины, чем величина а. Суммы распадаются таким образом на д части, из которых в одной а всегда больше Ь, и в другой всег меньше, при этом ясно, что для каждого члена одной части, име щего вид
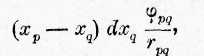
в другой должен находиться член:
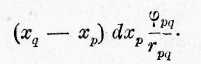
Если оба члена сложить, то получается
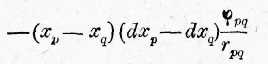
Еели сделать это соединение членов в суммы, сложить все суммы и при этом положить
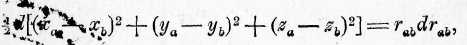
где мы получим:
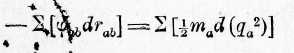
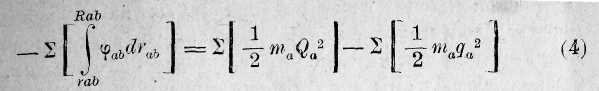
В
и Q точно так же, как г и q имеют соответствующие значения.Мы имеем здесь слева опять сумму затраченных работ, справа -умму живых сил всей системы, и мы можем теперь выразить этот закон так: во всех случаях движения свободных материальных точек под влиянием исходящих из них притягательных яли отталкивательных сил, величины которых зависят только от расстояния, уменьшение количества работы, которую можно от системы получить
1), всегда равно увеличению живой силы, и, наоборот, увеличение первой величины-уменьшению второй. Следовательно, всегда сумма существующих в системе потенциальной энергии2) и живых сил постоянна. В этой наиболее эбщей форме мы можем наш закон назвать принципом сохранения силы.При данном выводе закона ничего не изменится, если одна часть точек, которые мы отметим буквами
d, закреплена так, что qd = 0; тогда закон имеет вид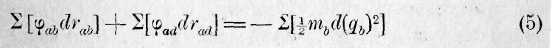

Остается только указать, в каких соотношениях стоит принцип со-сранения силы к общему закону статики, к так называемому прин-мпу возможных перемещений. Этот последний принцип вытекает 1рямо из наших уравнений 3 и 5. Если при определенном положе-fflii точки та
дол'жно существовать равновесие, другими словами, гели для того случая, когда эти точки находятся в покое, когда, следовательно, qa = О, это состояние остается неизменным, и, следо-зательно, все dqa = O, то из уравнения 3 следует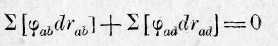
В этом уравнении под
dr нужно подразумевать те изменен расстояний, которые наступают при любых малых перемещена 1 точки та, допустимых при существующих условиях системы. Мы увидели в предыдущих выводах, что увеличение живой силы и, следо8 тельно, переход из покоя в движение, может быть произведено только за счет затраты потенциальной энергии1); последние уравц ния выражают соответственно этому, что при таких условиях, когда потенциальная энергия при всех возможных направлениях движет ' в первые моменты не уменьшается, система, находящаяся в по& ' в данный момент, остается в покое и в дальнейшем.Известно, что из установленных уравнений могут быть выведен все законы статики. Для природы действующих при этом сил являет; важным следующее следствие: представим себе, что вместо люб! малых перемещений точек
in берутся такие, какие могли бы сущ ствовать, если бы система была бы твердой системой, так что уравнении 7 все drab = O, отсюда следует, что отдельно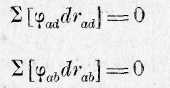
В этом случае условиям равновесия удовлетворяют как внешни так и внутренние силы. Поэтому, если определенная система в природы при действии определенных сил приведена в состоят равновесия, то равновесие не нарушается, 1)если мы отделью точки системы в их настоящих положениях
представим себе соед ненными неизменяемыми связями, и 2) если мы устраним силы, которыми точки действуют друг на друга. Из этого далее следуе если силы, с которыми действуют друг на друга две материальны точки, удерживаются в равновесии приложенными к ним двум внешними силами, то эти точки должны находиться в равновеся если вместо взаимодействующих между точками сил подставить твер дое соединение их между собой. Силы, которые действуют на точки твердой прямой линии, могут быть в равновесии только в том случае, если они действуют по направлению этой линии, и при это) равны и направлены в противоположные стороны. Таким ббразо" по отношению к силам, с которыми точки действуют друг на друга и которые должны быть равны внешним силам и направлен в противоположные стороны от них, следует, что эти силы действующие по линии, соединяющей точки, и являются таким образом притягательными или отталкивательными силами.