Attenenti alia

GALILEO GALILEI LINСEO,

Filosofoe Matematico primario del Sereniffimo Grand Ducadi Toscana.

Appreslbe Ji Elfevirii. м. d. c. xxxviti.

День Первый - 2. Галилео ГАЛИЛЕЙ - Galileo GALILEI. МАТЕМАТИЧЕСКИЕ ДОКАЗАТЕЛЬСТВА КАСАЮЩИЕСЯ ДВУХ НОВЫХ ОТРАСЛЕЙ НАУКИ, относящихся К механике и Местному Движению

С а л ь в. Если теперь сгибание линии под углами так, чтобы образовался квадрат или восьмиугольник или многоугольник с сорока, ста или тысячею сторон, представляется вам достаточным для действительного выявления тех четырех, восьми, сорока, ста или тысячи частей, которые, согласно вашему утверждению, содержались в потенции в первоначальной прямой линии, то, когда я образую из прямой линии многоугольник с бесконечным числом сторон, т. е. когда я сгибаю ее в окружность, не могу ли я с таким же правом утверждать, что я вызываю к действительности то бесконечное множество частей, которое первоначально, пока линия была прямой, содержалось в ней, по вашему утверждению, в потенции? Вы не можете отрицать, что подобное рассуждение не менее верно в отношении бесконечного множества частей линии, нежели в отношении четырех частей, образующих квадрат, или тысячи частей, образующих тысячеугольник, потому что в нем не нарушается ни одно из условий, имеющихся для многоугольника с тысячью или ста тысячами сторон. Последний, поставленный на одну из своих сторон и приложенный к прямой линии, соприкасается с ней этой стороной, т. е. одной стотысячной своей частью; круг, который представляет собою многоугольник с бесконечным числом сторон, соприкасается с прямой также одною из своих сторон, т. е. единственной точкой, отличной от других соседних, а потому отделенной и отграниченной от них не в меньшей степени, нежели отделена от соседних сторона любого многоугольника. Подобно тому как многоугольник, вращаемый на плоскости, образует последовательным наложением всех своих сторон прямую линию, равную его периметру, точно так же и круг, катящийся по плоскости, чертит соприкосновением бесчисленного множества точек прямую линию, равную его окружности. Теперь я не знаю, синьор Симпличио, согласятся ли со мною господа перипатетики, которых я поддерживаю в том, что всякое целое может быть разложено лишь на делимые части, так что, продолжая подобное деление последовательно, мы никогда не придем к концу, и признают ли они, что ни одно из их делений не будет последним и не может быть таковым, потому что для дальнейшего разложения всегда остаются делимые части, последнее же крайнее деление должно разложить делимое на бесконечное множество неделимых, чего, как я утверждаю, мы не можем достигнуть последовательным раздроблением на большее и большее количество частей. Предложенный же мною метод раздроблять и разделять бесконечность одним разом (искусственный прием, который следует приписать мне) должен и их успокоить и заставить принять, что всякое конечное тело состоит из абсолютно неделимых атомов. Этим дается также путь, более (надежный, нежели другие, чтобы выбраться из сложного лабиринта разных вопросов, к которым принадлежит, например, затронутый уже нами вопрос о связности частей твердого тела; приняв, что тела состоят из неделимых частиц, мы можем, как мне кажется, понять и явления разрежения и сгущения тел, не прибегая для объяснения первого к признанию пустых промежутков, а второго—к проникновению одних тел в другие.

Симпл. Не знаю, что сказали бы вам перипатетики; полагаю, что рассуждения ваши в большей своей части явились бы для них совершенно новыми и как таковые подлежали бы рассмотрению. Возможно, что они нашли бы возражения и ответы на те неясные пункты, которые я за краткостью времени и недостаточностью собственного критического отношения должен был оставить неразрешенными. Но оставим это теперь в стороне; мне очень хотелось бы узнать, каким образом введение последних неделимых облегчает понимание явления сгущения и разрежения, делая излишним в то же время признание образования пустоты или взаимного проникновения тел.

С а г р. Я также с большим интересом занялся бы Этим вопросом, для меня пока совершенно неясным; мне хотелось бы познакомиться с доводами Аристотеля в опровержение существования пустоты, о чем незадолго перед тем упомянул синьор Симпличио, а также и с вашим решением, в котором вы принимаете то, что он отрицает.

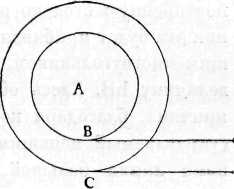
С а л ь в. Сделаем и то и другое. Что касается первого, то для понимания разрежения необходимо воспользоваться линией, описываемой малым кругом при вращении большого круга, которая оказалась больше, чем окружность этого малого круга; для понимания же сгущения мы покажем, как при вращении малого круга больший круг описывает прямую линию, меньшую по длине, чем его окружность; для более наглядного пояснения рассмотрим сперва, что происходит с соответствующими многоугольниками.

На чертеже, сходном с тем, которым мы пользовались раньше, изображены два многоугольника с общим центром L, именно ABC и HIK, и параллельные прямые НОМ и АВс, по которым будут катиться многоугольники. Удерживая вершину I малого многоугольника, повернем этот многоугольник так, чтобы сторона его IK совпала с прямой линией, при каковом движении точка К опишет дугу КМ, а сторона Ж совпадет с отрезком IM прямой. Теперь посмотрим, что сделается при этом со стороною ОВ большого многоугольника. Так как вращение совершается около точки I, то линия IB опишет своим концом В, двигающимся обратно, дугу ВЬ под параллельной линией сА, так что когда сторона KI совпадает с линией Ml, то сторона ВС совпадет с линией be, продвинувшись вперед лишь на отрезок Вс и отстав на отрезок, соответствующий дуге ВЬ, который отложится на линии ВА. При продолжении вращения подобным же образом меньший многоугольник опишет и пройдет по своей параллели линию, равную своему периметру; больший же многоугольник пройдет в то же время линию меньшую, чем его периметр, на величину ЬВ, повторенную столько раз, сколько у него сторон; линия рта будет приблизительно равна пройденной меньшим многоугольником, превышая последнюю лишь на величину ЬВ. Зд^есь обнаруживается, таким образом, причина, благодаря которой больший многоугольник (управляемый меньшим) не описывает своими сторонами линии большей, нежели описанная меньшим многоугольником; она заключается в том, что каждая сторона многоугольника покрывает часть пространства, уже пройденного предшествующей стороной.

Рассмотрим теперь два концентрических круга, описанных из центра А и покоящихся на двух параллельных линиях, соприкасаясь с ними—меньший в точке В, а больший—в точке С. При вращении меньшего круга точка В не будет оставаться некоторое время неподвижною, а линия ВС не будет перемещать назад точку С, как то имело место в многоугольнике, где точка I оставалась без движения, пока сторона KI не накладывалась на линию IM, а линия IB переносила точку В, т. е. конец стороны СВ, назад в точку Ь, так что сторона ВС принимала положение be, откладывая часть ВЬ на линии ВА и подвигаясь вперед только на часть Be, равную IM или стороне меньшего многоугольника; накладывание на пространство, занимаемое предшествующей стороной, излишков сверх величины стороны меньшего многоугольника и продвижение вперед лишь на остальную часть, равную стороне меньшего многоугольника, объясняло то явление, что линия, откладываемая большим многоугольником, равнялась линии, откладываемой меньшим. Но Здесь, если мы пожелаем применить то же рассуждение к явлению качения кругов, то должны будем сказать, что в то время как число сторон любого многоугольника выражается некоторой конечной величиной,—число сторон круга бесконечно; первые конечны и делимы, вторые же бесконечны и неделимы; концы сторон многоугольника при вращении остаются некоторый промежуток времени неподвижными, и промежуток этот равен времени полного обращения многоугольника, разделенному на число его сторон; в круге пребывание в покое концов бесчисленного множества его сторон продолжается одно мгновение, представляющее бесконечно малую часть конечного промежутка времени; соотношение здесь аналогично существующему между точкой и линией, которая также содержит бесконечное множество точек.

Обратное движение большего многоугольника происходит не на величину всей его стороны, но лишь на величину излишка большей стороны над меньшей, движение же вперед происходит на величину, равную стороне меньшего многоугольника; при движении кругов точка или сторона С при остановке на мгновение точки В также переносится назад на величину, равную излишку ее над стороною В, и продвигается вперед на величину, равную последней. В результате бесконечное множество неделимых сторон большего круга со своим бесконечным множеством бесконечно малых обратных движений, совершаемых во время бесконечно кратких остановок бесконечно большого числа сторон меньшего круга, и с бесконечным множеством продвижений вперед, равных, бесконечному числу сторон меньшего круга, описывает линию, равную описываемой меньшим кругом и содержащую бесконечное множество бесконечно малых наложений, образующих утолщение или, лучше сказать, уплотнение без проникновения одних конечных частей в другие, чего нельзя сделать с разделенной на конечные части линией, равной периметру какого-либо многоугольника; выпрямленный в одну линию, он не может сократиться без того, чтобы стороны его частью не налегли одна на другую или не проникли одна в другую. Такое уплотнение бесконечного множества бесконечно малых частиц без взаимного проникновения конечных частей и расхождение бесконечного множества бесконечно малых частин с образованием бесконечно малых или неделимых пустот представляет собою самое важное, что можно сказать об уплотнении и разрежении тел, не прибегая к допущению взаимного проникновения частей тела или к образованию пустот конечной величины. Если это вам нравится, то примите мои выводы; если же нет, то считайте их ложными так же, как и мои рассуждения, и поищите других объяснений, более удовлетворительных. Я только напомню вам при этом два слова: мы находимся в области бесконечных и неделимых.

С а г р. Признаюсь откровенно, что ваши соображения весьма остроумны и звучат для моих ушей, как нечто совершенно новое и чуждое; если, однако, природа на самом деле следует таким законам, то я не премину сказать: по отношению к вещам, недоступным чувству, верно то, что наиболее меня удовлетворяет. Чтобы не оставаться совершенно безгласным, я твердо придерживаюсь этого. Но, быть может, синьор Симпличио сможет осветить нам (с чем до сих пор я еще никогда не встречался) те объяснения, которые давали этому столь темному предмету философы. По правде сказать, все то, что мне довелось читать относительно уплотнения, было столь плотным, а относительно разрежения—столь тонким, что моя слабая голова не могла усвоить и постичь прочитанного.

Симпл. Я нахожусь в полном смущении, встречая серьезные затруднения и на том и на другом пути, в особенности же на новом. Согласно предложенному взгляду, унция золота может разредиться и образовать тело, объемом более земного шара, а с другой стороны, Земля может уплотниться и сжаться до размера ореха. Таким вещам я не верю, и полагаю, что вы сами тоже этому где верите. Ваши рассуждения и доказательства) суть чисто математические, отвлеченные и оторванные от всякой ощущаемой материи; я полагаю, что по отношению к физической материи и предметам, встречающимся в природе, выведенные законы не могут иметь приложения.

С а л ь в. Сделать для вас видимым невидимое—это, конечно, не в моих силах, и думаю, что вы не станете этого от меня и требовать. Но, насколько это доступно нашим чувствам, разве мы не можем убедиться в способности сильного разрежения хотя бы золота, которое вы только что назвали? Не знаю, случалось ли вам видеть, как мастера вытягивают золотую проволоку, у которой золото покрывает лишь поверхность, вся же внутренняя часть состоит из серебра. Вытягивают ее следующим образом: берут цилиндр или, проще сказать, стержень из серебра, длиною приблизительно в поллоктя и толщиною в три-четыре пальца, и покрывают его позолотою, накладывая листки сусального золота, которое, как вы знаете, настолько тонко, что от дуновения поднимается в воздухе; таких листков накладывается восемь-десять, не более того. Позолоченный таким образом стержень начинают затем с большой силой вытягивать, заставляя его проходить через отверстия в железной доске; пропуская его много и много раз через отверстия все меньшего диаметра, продолжают ртот процесс до тех пор, пока не получают нити столь же тонкой, как женский волос; и вся она остается с поверхности позолоченной. Предоставляю вам судить, сколь велика способность золота к утончению и расширению.

С и м п л. Я не вижу, чтобы из этой операции проистекало столь удивительное утончение вещества Золота, как вы того желаете. Во-первых, уже первоначальная позолота состояла из десяти золотых листков, что составляет значительную толщину; во-вторых, хотя серебро при вытягивании и утончении и прибавляется в длине, но зато уменьшается в толщине, так что изменение одного размера компенсируется изменением другого, и поверхность серебра увеличивается лишь настолько, что для покрытия ее золоту достаточно утончиться, может быть, лишь до пределов первоначального листка.

С а л ь в. Вы в достаточной мере ошибаетесь, синьор Симпличио, так как увеличение поверхности составляет квадратный корень из увеличения длины, как я могу это геометрически доказать.

Сагр. И от себя и от лица синьора Симпличио я прошу вас дать нам это доказательство, если, конечно, оно таково, что может быть нами понято.

С а л ь в. Попробую изложить его так, как оно приходит мне на память без подготовки. Само собою ясно, что первоначальный толстый серебряный стержень и длиннейшая вытянутая нить суть два равных по объему цилиндра, так как содержат то же количество серебра; поэтому если ялюкажу, какое отношение существует между поверхностями двух равных по объему цилиндров, то я докажу требуемое. Утверждаю, что отношение погерхностей двух равновеликих цилиндров, не считая площадей их оснований, равно корню квадратному из отношения их длин. Возьмем два равновеликих цилиндра, высота одного из коих равна АВ, а другого CD, и пусть линия Е будет средней пропорциональной между ними. Утверждаю, что поверхность цилиндра АВ, не считая площади его оснований, будет так относиться к поверхности цилиндра CD, также не считая площади его оснований, как линия АВ относится к линии Е, каковое отношение представляет собою корень квадратный из отношения АВ к CD. Разделим цилиндр АВ в F таким образом, чтобы высота части AF была равна CD. Так как отношение площадей оснований равновеликих цилиндров равно обратному отношению их высот, то площадь круга, лежащего в основании цилиндра CD, будет относиться к площади круга, лежащего в основании цилиндра АВ, как высота ВА к высоте CD; а так как площади кругов относятся между собой, как квадраты их диаметров, то и эти квадраты будут относиться, как ВА к CD. Но как ВА относится к CD, так относится и квадрат ВА к квадрату Е; следовательно, рти четыре квадрата пропорциональны между собою, а отсюда вытекает, что и стороны их пропорциональны, т. е. что линия АВ относится к линии Е так, как диаметр круга С к диаметру круга А. Но отношение диаметров равно отношению окружностей, а отношение окружностей равно отношению поверхностей цилиндров равной высоты. Таким образом отношение линии АВ к Е равно отношению поверхности цилиндра CD к поверхности цилиндра AF. Так как, однако, высота AF относится к АВ как поверхность AF к поверхности АВ, а высота АВ относится к линии Е как поверхность CD к поверхности AF, то обратно—отношение высоты AF к Е будет равно отношению поверхности CD к поверхности АВ, отношение же поверхности цилиндра АВ к поверхности цилиндра CD будет равно отношению линии Е к AF, т. е. к CD или же АВ к Е, каковое отношение представляет собою квадратный корень из отношения АВ к CD. А это и есть то, что требовалось доказать¹⁶.

Применим теперь то, что сейчас нами доказано, к нашему примеру, предположив, что позолоченный серебряный цилиндр имел не более поллоктя длины и три или четыре пальца толщины и, доведенный до тонкости волоса, образовал нить длиною в двадцать тысяч локтей (что вполне может быть достигнуто).

Мы найдем, что поверхность его увеличилась в двести раз против первоначальной, вследствие чего золотые листочки, наложенные первоначально в числе десяти, должны теперь покрыть поверхность в двести раз большую, так что толщина золотого слоя, покрывающего нить, будет составлять всего одну двадцатую часть толщины одного листка сусального золота. Подумайте, какова тонкость этого слоя, и можно ли представить себе таковую без огромного расхождения частей? Вместе с тем не доказывает ли этот опыт, что физическая материя состоит из бесконечного множества малых частиц? Впрочем, этому можно привести и другие, еще более веские и убедительные примеры.

С а г р. Доказательство кажется мне столь прекрасным, что если бы даже оно и не имело силы убедить нас в том, для чего оно было приведено (и чего, как мне кажется, оно в значительной мере достигает), то оно все же вполне вознаградило нас за то краткое время, которое мы потратили, чтобы его выслушать.

С а л ь в. Раз я вижу, что вы столь высоко цените геометрические доказательства, дающие нам надежную опору, то я познакомлю вас с другим предложением, дающим ответ на довольно интересный вопрос. Ранее мы рассматривали цилиндры равного объема, но разной высоты или длины; теперь мы займемся цилиндрами, имеющими равную поверхность, но различную длину; отмечу, что речь будет итти лишь о боковых поверхностях, основания же, как верхние, так и нижние, в расчет не принимаются. Утверждаю, что объемы прямых цилиндров, поверхности которых, не считая площадей оснований, равны, обратно пропорциональны их высотам.

Пусть АЕ и CF будут два цилиндра с равными боковыми поверхностями, причем высота второго CD больше высоты первого АВ. Утверждаю, что объем цилиндра АЕ так относится к объему цилиндра CF, как высота CD к высоте АВ. Так как поверхность CF равна поверхности АЕ, то объем цилиндра CF будет меньше объема цилиндра АЕ. В самом деле, если бы они были равны, то по доказанному ранее положению его поверхность превосходила бы поверхность цилиндра АЕ; то же имело бы место в еще большей степени, если бы цилиндр CF был более цилиндра АЕ. Предположим теперь, что имеется цилиндр ID, равновеликий цилиндру АЕ; согласно доказанному выше, поверхность этого цилиндра ID относится к поверхности АЕ, как высота его IF к средней пропорциональной между IF и АВ. Так как, однако, поверхность цилиндра АЕ равна поверхности CF и так как поверхность цилиндра ID относится к поверхности CF, как высота IF к высоте CD, то высота CD есть также среднее пропорциональное между IF и АВ. Так как сверх того цилиндр ID равен цилиндру АЕ, то они имеют одно и то же отношение их к цилиндру CF; но ID относится к CF, как высота IF к CD; следовательно, отношение цилиндра АЕ к цилиндру CF будет равно отношению линии IF к CD, т. е. отношению CD к АВ, что и требовалось доказать.

Отсюда можно вывести объяснение одного явления, которое люди часто наблюдают не без удивления. Если из куска холста, у которого длина больше ширины, делается мешок для зерна с дном из деревянной доски, как это обычно принято, то спрашивается, почему мешок будет более вместимым, если короткую сторону направить вверх, а более длинной охватить деревянное дно, нежели если сделать наоборот. Предположим, что холст имеет в ширину шесть и в длину двенадцать локтей; если длинная сторона холста в двенадцать локтей будет охватывать дно, а высота мешка будет равняться шести локтям, то мешок будет более емким, нежели в том случае, когда охватывать дно будет короткая сторона в шесть локтей, а высота мешка будет составлять двенадцать локтей. То, что было ранее доказано, позволяет не только составить общее суждение о том, в каком случае объем будет больше, но и показать, насколько один объем будет больше или меньше другого; он будет во столько раз больше, во сколько высота его ниже, и во столько раз меньше, во сколько она выше. В приведенном нами примере кусок холста имеет длину, в два раза превышающую его ширину; вместимость мешка, обращенного к основанию коротг

кой стороной и сшитого по длине, будет в два раза меньше вместимости мешка, сшитого по ширине. Точно так же, если имеем подобие плетеной циновки, длиною в двадцать пять локтей и шириною в семь локтей, и хотим сделать из нее корзину, то объемы корзин, сшитых по длине и по ширине циновки, будут относиться друг к другу, как семь к двадцати пяти.