Attenenti alia

GALILEO GALILEI LINСEO,

Filosofoe Matematico primario del Sereniffimo Grand Ducadi Toscana.

Appreslbe Ji Elfevirii. м. d. c. xxxviti.

ОТРАСЛЕЙ НАУКИ

С а г р. Таким путем мы с особым удовлетворением постепенно приобретаем новые познания, не лишенные и практической пользы. В отношении только что Затронутого положения я полагаю, что среди лиц, мало знакомых с геометрией, едва ли найдется четыре процента таких, которые сразу же не сделают ошибки и не скажут, что тела, имеющие равные поверхности, равны и во всем прочем. В подобную же ошибку впадают и при определении площадей, сравнивая, как то часто случается, величину различных городов на основании длины их обводов и полагая, что об их сравнительной величине можно судить, зная, во сколько раз обвод одного более обвода другого. При этом упускается из виду, что хотя обвод одного может равняться обводу другого, но пространство, ограниченное равными линиями, может быть в одном случае Значительно больше, нежели в другом. Это имеет место в отношении не только неправильных фигур, но и правильных, из коих те, которые имеют большее число сторон, имеют и большую площадь, так что_г в конце концов, круг как многоугольник с бесконечным числом сторон охватывает площадь большую, чем все остальные многоугольники, равного с ним обвода. Я с особым удовольствием вспоминаю доказательство этого положения, которое я нашел при изучении „Сферы" Сакробоско и соответствующих ученейших комментариев ¹⁷.

С а л ь в. Совершенно верно. Пользуясь подобным же случаем, я нашел очень простой способ доказать, что из всех правильных фигур с равным периметром круг имеет наибольшую площадь, которая у многоугольников, вообще, тем более, чем больше число их сторон.

С а г р. Так как я очень люблю доказательства из вестных, положений, тонкие и далекие от обычных, то я очень прошу вас познакомить меня с вашим доказательством.

С а л ь в. Это можно сделать в нескольких словах на основании следующей теоремы:

Крут есть среднее пропорциональное между двумя любыми правильными подобными многоугольниками, один из которых описан вокруг него, а другой— изопериметричен кругу. Будучи меньше всех описанных многоугольников, круг в то же время больше всех изопериметричных ему многоугольников. Далее, из описанных многоугольников те, которые имеют большее число углов, меньше тех, которые имеют их меньшее число; наоборот, из изопериметричных кругу многоугольников больше те, число углов у которых больше.

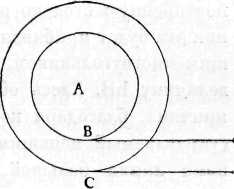
 Пусть из двух подобных многоугольников А и В первый—А—описан около круга А, другой же—В— изопериметричен кругу; утверждаю, что круг является средним пропорциональным между ними. Круг Этот равен по площади (если радиусом его будет АС) такому прямоугольному треугольнику, одна из сторон которого, прилегающих к прямому углу, равна АС, другая же равна окружности. Так как в то же время многоугольник А равен прямоугольному треугольнику, одна из прилетающих к прямому углу сторон которого равна той же линии АС, другая же равна периметру этого многоугольника, то ясно, что площадь описанного многоугольника относится к площади круга, как периметр этого многоугольника к окружности круга или равному окружности периметру другого многоугольника В. Но отношение многоугольников А и В равно отношению квадратов их периметров (так как фигуры эти подобны); следовательно, круг А есть среднее пропорциональное между многоугольниками А и В. Так как многоугольник А больше круга А, то ясно, что круг А должен быть больше многоугольника В, имеющего равный с ним периметр, а следовательно, и больше всех изопериметричных ему правильных многоугольников.

Что касается другой части предложения, т. е. что из многоугольников, описанных вокруг данного круга, имеющие меньшее число сторон больше тех, число сторон коих больше, и что, наоборот, из изопериметричных многоугольников больше те, число сторон коих больше, то она доказывается следующим образом. К кругу, имеющему центр в точке О и радиус ОА, проведем касательную AD, на которой отложим отрезок AD, равный, например, половине стороны описанного пятиугольника, и отрезок АС, равный половине стороны такого же семиугольника. Проведем прямые OGC, OFD и опишем из центра О радиусом, равным линии ОС, дугу ECI. Так как треугольник DOC больше сектора ЕОС, а сектор COI больше треугольника СОА, то отношение треугольника DOC . к треугольнику СОА будет больше отношения сектора ЕОС к сектору COI, или сектора FOG к сектору GOA. Суммируя и обращая, получим, что отношение треугольника DOA к сектору FOA будет больше отношения треугольника СОА к сектору GOA и отношение десяти треугольников DOA к десяти секторам FOA будет больше отношения четырнадцати треугольников СОА к четырнадцати секторам GO А; таким образом отношение к кругу описанного пятиугольника будет больше отношения к тому же кругу описанного семиугольника и, следовательно, пятиугольник будет больше семиугольника. Представим себе теперь семиугольник и пятиугольник, имеющие периметры, равные окружности данного круга; утверждаю, что семиугольник больше пятиугольника. Так как круг является средним пропорциональным между пятиугольником, описанным около него, и пятиугольником, имеющим равный с окружностью периметр, а также и средним пропорциональным между описанным и изопериметричным семиугольником, и так как доказано уже, что описанный пятиугольник больше описанного семиугольника, то отношение пятиугольника к кругу будет больше отношения к нему же семиугольника; поэтому отношение круга к изопериметричному с ним пятиугольнику будет больше отношения его к такому же семиугольнику; следовательно, пятиугольник меньше изопериметрич-ного семиугольника, что нам и требовалось доказать.

Сагр. Прекрасное доказательство, и весьма тонкое ¹⁸. Но мы, кажется, слишком углубились в область геометрии. Мы собирались рассмотрзть затруднения, выдвинутые синьором Симпличио и заслуживающие большого внимания. В особенности затруднительной представляется мне проблема сгущения.

С а л ь в. Если сгущение и разрежение представляют собою явления противоположные, то, видя чрезвычайное разрежение, нельзя отрицать возможности столь же большого сгущения. А чрезвычайное разрежение, совершающееся к тому же почти мгновенно, что делает его еще более удивительным, мы можем наблюдать ежедневно. Не представляется ли примером чрезвычайного разрежения превращение малого количества артиллерийского пороха в огромный объем огня? И как велико к тому же, даже почти безгранично, распространение возникающего при этом света? И если бы этот огонь и этот свет опять соединились, что не представляется невозможным, так как только что перед тем они заключались в самом малом объеме, то как велико было бы сгущение? Подумав, вы найдете тысячи случаев разрежения, которые гораздо легче наблюдать, нежели случаи сгущения, так как плотное вещество легче поддается нашему воздействию и доступнее нашим чувствам. Если мы возьмем дерево, то мы можем превратить его в огонь и свет, но мы бессильны сгустить эти огонь и свет и обратить их в дерево; мы наблюдаем как плоды, цветы и тысячи других плотных тел частью превращаются в запах, но нам не удалось сгустить атомы, производящие запах, в плотные благоухающие тела. Там, где недостает чувственного' наблюдения, необходимо прибегать к помощи размышления, которое дает нам возможность понять явление разрежения и растворения не только твердых тел, но и сгущения веществ нетвердых и даже самых тонких. Приступим же к рассмотрению того, как могут происходить сгущение и разрежение таких тел, которые способны к сгущению и разрежению, не прибегая при этом к помощи предположения пустоты и проницаемости тел. При э.том не исключена возможность, что в природе существуют такие вещества, с которыми данного явления не происходит, и то, что вы признаете затруднительным или невозможным, и в действительности иногда не имеет места, В заключение, синьор Симпличио, я много потрудился над тем, чтобы наперекор вам, господам философам, представить, каким образом могут происходить сгущение и разрежение без допущения проницаемости тел или существования пустых пространств — допущений, которые вы отрицаете и отклоняете, тогда как, если бы вы пожелали их признать, вы не нашли бы во мне столь упорного противника. Итак, или примите эти Затруднительные допущения, или согласитесь с моими объяснениями, или же, наконец, найдите более удовлетворительные.

С а г р. Взаимное проникновение тел я совершенно отрицаю, сходясь в этом с философами-перипатетиками. Что же касается пустоты, то мне хотелось бы внимательно рассмотреть как доводы Аристотеля, направленные против ее допущения, так и ваши, синьор С а л ь виати, с ним несогласные; синьор Симпличио будет добр точно изложить доводы философа, а вы, синьор С а л ь виати, представьте свои возражения.

С и м п л. Аристотель, насколько я помню, оспаривает мнение некоторых древних философов, которые вводили пустоту как необходимое условие движения, говоря, что последнее невозможно без первой. Оспаривая такое положение, Аристотель доказывает, наоборот, что существование движения (как можно видеть) противоречит допущению пустоты. Его доказательство таково. Он рассматривает два случая: один—движение тел различного веса в одинаковой среде; другой—движение одного и того же тела в различных средах. Относительно первого случая он утверждает, что тела различного веса движутся в одной и той же среде с различными скоростями, которые относятся между собою, как веса тел, так что, например, если одно тело в десять раз тяжелее другого, то и движется оно в десять раз быстрее. Относительно второго случая он принимает, что скорость движения одного и того же тела в различных средах различна и обратпо пропорциональна степени густоты или плотности среды; таким образом, если предположить, что степень плотности воды равна десятикратной плотности воздуха, то движение в воздухе должно совершаться в десять раз быстрее, чем в воде. Из этого второго положения он выводит дальнейшее доказательство в следующей форме. Так как разреженность пустоты бесконечно отличается от плотности пространства, заполненного хотя бы тончайшим веществом, то движущиеся тела, проходящие определенное расстояние в заполненном пространстве в некоторый промежуток времени, должны были бы передвигаться в пустоте мгновенно; но мгновенное движение невозможно; поэтому невозможно и образование пустоты вследствие движения.

С а л ь в. Аргумент, как видите, приводится „a d h о m i n e m", т. е. против тех, кто полагал, что пустота необходима для движения. Поэтому, если я сочту аргумент доказательным, но вместе с тем признаю, что в пустоте движение не совершается, то существование пустоты в абсолютном смысле—без отношения к движению—этим не будет опровергнуто. Но рассуждая в духе этих древних и рассматривая, насколько убедительны доводы Аристотеля, следует, как мне кажется, возражать против его положений, отрицая оба. Во-первых, я сильно сомневаюсь, чтобы Аристотель видел на опыте справедливость того, что два камня, из которых один в десять раз тяжелее другого, начавшие одновременно падать с высоты, предположим, ста локтей, двигались со столь различной скоростью, что в то время как более тяжелый достиг бы Земли, более легкий прошел бы всего 10 локтей.

С и м п л. Из ваших слов выходит, что вы производили подобные опыты, потому что вы говорите: „видел более тяжелый", а видеть можно только тогда, когда производишь опыты.

С а г р. Но я, синьор Симпличио, не производивший никаких опытов, уверяю вас, что пушечное ядро весом в сто, двести и более фунтов не опередит и на одну пядь мушкетной пули весом меньше полфунта при падении на землю с высоты двухсот локтей.

С а л ь в. Да и без дальнейших опытов путем краткого, но убедительного рассуждения мы можем ясно показать неправильность утверждения, будто тела, более тяжелые, движутся быстрее, нежели более

легкие, подразумевая тела из одного и того же вещества, т. е. такие, о которых говорит Аристотель. В самом деле, скажите мне, синьор Симпличио, признаете ли вы, что каждому падающему твердому телу присуща от природы определенная скорость, увеличить или уменьшить которую возможно только путем введения новой силы или препятствия?

С и м п л. Я не сомневаюсь в том, что одно и то же тело в одной и той же среде имеет постоянную скорость, определенную природой, которая не может увеличиться иначе, как от приложения новой силы, или уменьшиться иначе, как от препятствия, замедляющего движение.

С а л ь в. Таким образом, если мы имеем два падающих тела, естественные скорости которых различны, и соединим движущееся быстрее с движущимся медленнее, то ясно, что движение тела, падающего быстрее, несколько задержится, а движение другого несколько ускорится. Вы не возражаете против такого положения?

С и м п л. Думаю, что это вполне правильно.

С а л ь в. Но если pro так, и если вместе с тем верно, что большой камень движется, скажем, со скоростью в восемь „градусов", тогда как другой, меньший,—со скоростью в четыре „градуса", то соединяя их вместе, мы должны получить скорость, меньшую восьми „градусов"; однако! два Камня, соединенные вместе, составляют тело больше первоначального, которое имело скорость в восемь „градусов"; следовательно, выходит, что более тяжелое тело движется с меньшей скоростью, чем более легкое¹⁹; а это противно вашему предположению. Вы видите теперь, как из положения, что более тяжелые тела движутся с большей скоростью, чем легкие, я мог вывести заключение, что более тяжелые тела движутся менее быстро.

Симпл. Я чувствую себя совершенно сбитым с толку. Мне кажется, что малый камень, присоединенный к большому, увеличивает вес последнего; но увеличивая вес, он- должен если не увеличить скорость, то во всяком случае не уменьшить ее.

С а л ь в. Здесь вы совершаете новую ошибку, синьор Симпличио, так как неправильно, что малый камень увеличивает вес большого.

С и м п л. Ну, это уже превосходит мое понимание.

С а л ь в. Нисколько, все будет понятно, как только я избавлю вас от заблуждения, в которое вы впали. Дело в том, что необходимо делать различие между телами, пребывающими в покое и находящимися в движении. Большой камень, взвешиваемый на весах, приобретает больший вес от наложения на него не только другого камня: положенная на него связка пакли увеличивает его вес на шесть-десять унций, которые весит сама пакля. Но если вы заставляете камень свободно падать с некоторой высоты вместе с наложенной на него паклей, то думаете ли вы. что при движении пакля будет давить на камень и тем увеличивать скорость его движения, или что она

его замедлит, поддерживая камень? Мы чувствуем тяжесть на плечах, когда сопротивляемся движению, к которому стремится давящая тяжесть; но если мы бы опускались с такою же скоростью, с какою перемещается свободно падающий груз, то каким образом тяжесть могла бы давить на нас? Не видите ли вы, что это подобно тому, как если бы мы хотели поразить копьем кого-либо, кто бежит впереди нас с равною или большею скоростью? Выведите из этого заключение, что при свободном и естественном падении малый камень не давит на больший и, следовательно, не увеличивает его веса, как то бывает при покое.

С и м п л. Но если положить больший камень на меньший?

С а л ь в. Он увеличил бы вес меньшего, если бы движение его Сыло более быстрым; но мы уже нашли, что если бы меньший двигался медленнее, то он замедлил бы отчасти движение большего; таким образом целое двигалось бы медленнее, будучи больше своей части, что противно нашему положению. Выведем из всего этого, что тела большие и малые. имеющие одинаковый удельный вес, движутся с одинаковой скоростью. -

Симпл. Ваше рассуждение, действительно, прекрасно; однако мне все же трудно поверить, что крупинка свинца должна падать с такой же быстротою, как пушечное ядро.

С а л ь в. Скажите лучше—песчинка с такой же быстротой, как мельничный жернов. Я не хотел бы, синьор Симпличио, чтобы вы поступали как многие другие, отклоняя беседу от главного вопроса, и придирались к выражению, в котором я допустил отклонение от" действительности на один волосок, желая скрыть за этой небольшой погрешностью ошибку другого, грубую, как якорный канат. Аристотель говорит: „железный стержень, весом в сто фунтов, падая с высоты ста локтей, упадает на землю, в то время как другой, весом в один фунт, пройдет пространство в один локоть". Я утверждаю, что оба упадут одновременно. Проделав опыт, вы найдете, что больший опередит меньший на два пальца, так что когда больший упадет на землю, то меньший будет от нее на расстоянии толщины двух пальцев. Этими двумя пальцами вы хотите закрыть девяносто девять локтей Аристотеля и, говоря о моей небольшой ошибке, умалчиваете о громадной ошибке другого. Аристотель говорит, что тела различного веса движутся в одной и той же среде (поскольку движение происходит от силы тяжести) со скоростями, пропорциональными их весу, и приводит в пример тела, на которых можно проследить чистое, абсолютное влияние веса, отбрасывая в сторону все другие соображения как относительно формы, так и относительно других малозначащих моментов, каковые легко подвергаются воздействию среды, изменяющей простое действие силы тяжести; так, мы видим, что золото-вещество, тяжелейшее из всех других,—будучи превращено в тончайшие листки, носится в воздухе; то же делается с ним, когда кусок его обращен в тончайший порошок. Но если вы желаете доказать общее положение, то вам следует показать, что пропорциональность скоростей наблюдается во всех тяжелых телах, так что камень в двадцать фунтов весом надает в десять раз быстрее, чем камень весом в два фунта; а это, как я утверждаю, неверно: падая с высоты пятидесяти—ста локтей, оба они достигнут земли в один и тот же момент.

С и м п л. Быть может, при падении с большей высоты, хотя бы в тысячу локтей, обнаружилось бы то, чего нельзя заметить при меньших высотах?

С а л ь в. Если вы полагаете, что Аристотель так думал, то вы приписываете ему другую ошибку, даже ложь. Так как на земле мы не находим столь больших вертикально подымающихся высот, то ясно, что Аристотель не мог производить с ними опытов; а между тем, он хочет убедить нас, что делал опыты, говоря, что можно видеть такое явление.

Симпл. На самом деле Аристотель пользуется не Этим принципом, а другим, с которым, я полагаю, не связано таких затруднении.

С а л ь в. Второе утверждение не менее ложно, нежели первое. Меня удивляет, как вы сами не замечаете его неправильности и не видите, что если бы было правильно, что одно и то же тело в средах различной тонкости или плотности, словом, разной сопротивляемости, например в воде и в воздухе, движется в воздухе со скоростью большей, нежели в воде, во столько же paз, во сколько плотность воздуха меньше плотности воды, то из этого вытекало бы, что все тела, падающие в воздухе, опускаются ко дну также п в Воде, что совершенно ложно, так как существуют многие тела, которые не только не тонут в воде, но даже поднимаются в ней на поверхность.

С и м п л. Я не вижу необходимости в вашем заключении и скажу, что Аристотель имел в виду такие тяжелые тела, которые опускаются как в одной, так и другой среде, а не такие, которые в воздухе падают, а в воде поднимаются кверху.

С а л ь в. Вы выдвигаете в защиту философа такие аргументы, которыми он, конечно, не воспользовался бы, чтобы не увеличивать своей первоначальной ошибки. Скажите мне, находится ли плотность воды или, вообще, причина, замедляющая движение в ней, в каком-либо определенном отношении к плотности воздуха, где эта замедляющая причина меньше; если находится, то определите примерно это отношение.

С и м п л. Конечно, находится, и допустим, что это отношение равно десяти; таким образом скорость твердого тела, опускающегося в том и в другом веществе, будет в воде в десять раз меньше, чем в воздухе.

С а л ь в. Возьмем теперь одно из таких тел, которые падают в воздухе, но не тонут в воде; пусть Это будет кусок дерева; предоставляю вам назначить по вашему усмотрению скорость его движения в воздухе.

Симпл. Предположим, что он падает со скоростью двадцати градусов.

С а л ь в. Прекрасно. Очевидно, что такая скорость будет находиться к другой—меньшей скорости в таком же отношении, какое имеет плотность воды к плотности воздуха, почему меньшая скорость будет равняться двум градусам. Отсюда, рассуждая последовательно, мы должны были бы заключить, согласно правилу Аристотеля, что деревянный шар, который падает в воздухе, в десять раз менее плотном, нежели вода, со скоростью двадцати градусов, должен опускаться в воде со скоростью двух градусов, а не подниматься со дна на поверхность, как то происходит на самом деле. Я не думаю, чтобы вы стали утверждать, будто подниматься в воде и опускаться ко дну со скоростью двух градусов для дерева одно и то же. Так как кусок дерева в воде не тонет, то вы, надо полагать, допустите вместе со мною, что можно выбрать кусок вещества иного, нежели дерево, который бы опускался в воде со скоростью двух градусов.

С и м п л. Конечно, допускаю, но вещество эю должно быть значительно тяжелее дерева.

С а л ь в. Именно такое я и ищу. Но спрашивается, с какой скоростью будет падать в воздухе этот второй кусок, опускающийся в воде со скоростью двух градусов? Па этот вопрос вы должны будете ответить (пользуясь правилом Аристотеля), что он будет падать со скоростью двадцати градусов; но ту же скорость в двадцать градусов вы уже приписали куску дерева; следовательно, и этот кусок и другой, значительно более тяжелый, будут двигаться в воздухе с одинаковой скоростью. Каким же образом мог бы согласовать философ этот вывод с другим своим положением, что тела разного веса в одной и той же среде движутся с различными скоростями, пропорциональными их весу? Отвлекаясь теперь от глубоких размышлений, позвольте спросить, каким образом не замечаете вы совершенно очевидных и часто встречающихся явлений, когда из двух тел, движущихся в воде, одно перемещается, например, во сто раз быстрее другого, тогда как при падении в воздухе скорость одного превышает скорость другого едва ли на одну сотую долю? Так, мраморное яйцо опускается в Ьоде в сто раз быстрее куриного яйца; при падении же л воздухе с высоты двадцати локтей оно опережает куриное яйцо едва ли на четыре пальца. Существуют тела, которые в воде опускаются за три часа на глубину десяти локтей, каковое пространство в воздухе они пробегают за один-два удара пульса, тогда как другие (например свинцовый шарик) падают в воздухе со скоростью приблизительно в два раза большей той, с которой они тонут в воде²⁰. Теперь, синьор Симпличио, вы, без сомнения, сознаете, что вам нечего более мне возразить. Согласимся же на том, что приведенный ранее аргумент не заключает в себе ничего опровергающего существование пустоты; а если бы он и был убедительным, то им опровергалось бы лишь допущение таких больших

пустот, которые ни я, ни древние не представляли себе естественно существующими и которые могут быть созданы искусственно путем применения силы, как то доказывается опытами, на которых, однако, было бы слишком долго теперь останавливаться.

Carp. Так как синьор Симпличио хранит молчание, то я воспользуюсь моментом, чтобы сказать несколько слов. Вы совершенно ясно доказали, что тяжелые тела различного веса движутся в одной и той же среде не с различными скоростями, пропорциональными их весу, а с одинаковой скоростью; я полагаю, что это относится к телам из одного и того же вещества или, лучше сказать, одинакового удельного веса, но не к телам разного удельного веса (так как я не думаю, чтобы вы утверждали, будто кусок пробки падает с такою же скоростью, как кусок свинца); далее, вы ясно доказали, что неправильно принимать, будто скорость движения одного и того же тела в различных средах изменяется в той же пропорции, как сопротивляемость среды; мне очень хотелось бы знать, какие же отношения наблюдаются в действительности в том и другом случае?

С а л ь в. Вопросы очень интересные, и я много о них думал; я сообщу вам кое-что из того, к чему я пришел после долгих размышлений. После того, как я убедился, что неправильно, будто одно и то же тело движется в различных средах с различными скоростями, обратно пропорциональными сопротивляемости Среды, и что не менее неправильно и то, будто в одной и той же среде тела различного веса движутся с различными скоростями, пропорциональными их весу (даже если учесть разность в удельном весе), я начал комбинировать рти два явления, наблюдая, что происходит с телами различного веса в средах различной сопротивляемости. При этом я нашел, что* разница в скорости всегда значительно больше в средах более плотных, нежели в редких; разница эта доходит до того, что из двух тел, падающих в воздухе со скоростями, отличающимися лишь на самую малость, в воде одно движется в десять раз быстрее другого; точно так же есть тела, которые, быстро падая в воздухе, в воде не тонут, но остаются лишенными движения или еще более—поднимаются кверху: можно легко найти дерево такого сорта, что суковатые части или корни его будут оставаться в воде в любом месте без движения, тогда как в воздухе они быстро падают.

Саг р. Я много раз с большим усердием старался: ' увеличить вес куска воска, который сам по себе не тонет, прибавляя к нему песок так, чтобы он, сравнявшись по весу с водой, мог оставаться в ней без движения; но, несмотря на все старания, это мне не удавалось; не знаю, существует ли другое твердое вещество, настолько близкое к воде по удельному весу, чтобы оно, будучи погружено в воду, могло оставаться в ней без движения.

С а л ь в. В этом отношении, равно как и в тысяче других, многие животные совершеннее нас. В вашем

случае хорошим примером могли бы служить рыбы. Они столь искусны в подобных упражнениях, что по желанию могут сохранять равновесие в воде и притом не только чистой, но и значительно измененной по своей природе или благодаря примеси речного ида или соли, создающих существенную разницу; это совершается ими с такой ловкостью, что они могут, яе двигаясь, пребывать в воде в покое в любом месте. . ^Этого, как я полагаю, они достигают при помощи данного им природою для этой цели органа—пузыря, находящегося в их теле и соединяющегося довольно узким проходом со ртом. Сообразно цели, они то выталкивают из пузыря часть содержащегося в нем воздуха, то, поднимаясь на поверхность, вновь поглощают последний, делаясь, по желанию то легче воды, то одинакового с нею веса.

С а г р. Несколько иной проделкой я обманул, однажды, нескольких своих друзей, похваставшись им. что довел воск до равного с водою веса. Я зачерпнул сначала в сосуд соленой воды, затем налил сверху пресной и показал им, что кусок воска “становился посредине; погруженный на дно или поднятый на поверхность, он опять возвращался в середину.

С а л ь в. Это опыт далеко не бесполезный. Когда медики говорят о различных свойствах воды и, между прочим, о большей легкости или тяжести одной по сравнению с другой, то посредством такой палочки, стоящей по тяжести, так сказать, на границе между опусканием и поднятием в зоде, можно обнаружить лаже незначительную разницу в весе различных вод: в одной шарик тонет, в другой, более тяжелой,— поднимается. Прибор этот настолько чувствителен, что прибавления двух гран соли к шести фунтам воды достаточно, чтобы поднять со дна на поверхность палочку, которая ранее опустилась. Скажу вам, далее, в доказательство чувствительности этого опыта, а также в подтверждение того, что вода не оказывает никакого сопротивления разделению, что подобное же явление производит не только примесь к воде какого-нибудь более тяжелого вещества, но и нагревание или охлаждение ее; чувствительность столь велика, что прибавления к шести фунтам воды четырех капель горячей или холодной воды достаточно, чтобы заставить шарик двигаться вниз и вверх: Он тонет при прибавлении теплой воды и, наоборот, поднимается при прибавлении холодной. Отсюда вы можете видеть, как заблуждались философы, наделявшие воду вязкостью или связностью, заставляющей ее противиться разделению или проникновению.

С а г р. Я видел много убедительных соображений по Этому поводу в одном трактате нашего Академика; и все-таки у меня осталось некоторое сомнение, которое я не могу преодолеть. Если между частицами воды нет никакого сцепления или связности, то каким образом могут удерживаться, например на листьях капусты, довольно большие капли воды без того, чтобы не расплываться и не.расходиться²¹?