Dynamics of a single atom transition and problem of quantum jumps
A mechanism of quantum jumps for an atom which is being in a process its proceeding from one stationary energy state to another one is rather vague up to now. Some principle questions are arising to perplex most of the researchers when they deal with a single atom problem. For example:
What is a real physical mechanism of a quantum jump?
Where is the atom just as it leaves one stationary state but have not got at the other one yet?
How does a photon chance to find itself into the atom?
Whether is the photon really indivisible?
This work do not claim answering these points finally but the author would like to show some discrepancies arising while in discussions of the single atom behavior one attempt to combine the photon indivisibility principle with the energy conservation law.
Generally speaking in order to get it these points for the single atom , one should obviously coordinate an adequate theory, reliable experiments and philosophy based on causality with common sense. It well known that the quantum theory can not possibly get along in explaining a deterministic behavior of the single atom during its quantum jumps. As a matter of fact , both the Schroedinger's and its alternative Hysenberg's mechanisms of a quantum jump let us get no satisfactory explanation because both of them are based on a probability conception. Such an approach is obviously to except a determinism absolutely while we consider a concrete single atom as a real object. Certainly, the quantum approach is a very nice tool if we study incoherent behavior a lots of atoms, namely the atomic systems prepared by accidental way. However many a time the results obtained in such experiments are erroneously ascribed to the concrete single atom behavior instead of to apply this to an effective average atom which is identically indiscernible one, as it is required by the quantum principle itself. This I believe is a principle reason to many misunderstandings.
Experiments with the single atom are rather hard and became accessible only recently. There is ,however, another more preferable way to get realistic information about a single atom behavior. I mean that we can study a behavior of a great number of atoms density of which is so small (dilute crystals, gases) that the atoms can practically no influence each other. Preparing such ensembles coherently and suppressing relaxation channels we can deduce conclusions about the single atom behavior from a coherent response of the noninteracting atoms in the ensemble.
A great deal of the experiments based on coherency of atomic oscillations are available at present (photon echo, transient light induced gratings, free induction decay and the other optical transients1).Using such phenomena one can trace a dynamic behavior of the atom while it is proceeding from one
stationary state to another. Usually to adequately describe the optical transients the semiclassical approach is applied more successfully than the quantum electrodynamics. It turned out to make no sense in using the photon conception at all in order to fit the transient experimental data with the theory and real physical sense. Moreover the photon indivisibility principle as a main point of quantum electrodynamics appears to come to contradiction with the energy conservation law. In order to prove this assertion holds true let us consider a dynamics of energy behavior for a single atom in the well-known problem of a field-atom interaction. Let the atom be in the lowest energy state and subjected by a resonant step-like optical field with frequency
 and electric field strength
and electric field strength 
|
|
(1) |
the unit field strength vector  .
.
An isolated atom (in a dilute gas or a solid as an impurity) can be considered as a two-level system capable of being excited through an interaction of the electric dipole moment with an external optical field [1].The properties of a two level system are completely specified by the wave function
|
|
(2) |
which is a linear superposition of the 1 and 2 stationary states (  - spin-down and spin-up eigenstates).The probability amplitudes
- spin-down and spin-up eigenstates).The probability amplitudes  are continuous functions on time,
are continuous functions on time, - eigenvalues of energy of the two level atom (stationary states).
- eigenvalues of energy of the two level atom (stationary states).
When the atom subjected by the field (1) an evolution of its
wave function  is governed by the nonstationary Schroedinger's equation
is governed by the nonstationary Schroedinger's equation
|
|
(3) |
where  ,
,  is the field-free Hamiltonian and
is the field-free Hamiltonian and  - the interaction operator in electric dipole approximation due to the external field
- the interaction operator in electric dipole approximation due to the external field 
|
|
(4) |
where  is the dipole moment operator of the transition and
is the dipole moment operator of the transition and  -
-
the electric field strength (1).
Following the substitution of (1), (2) and (4) into Eq.(3) we arrive to the well-known equations for the probability amplitudes [2]
|
|
(5) |
where the detuning from resonance is 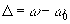 at the transition frequency equaled to
at the transition frequency equaled to , the resonant Rabi frequency is
, the resonant Rabi frequency is  , p - a projection of the dipole moment matrix element on the unit field strength vector
, p - a projection of the dipole moment matrix element on the unit field strength vector  .
.
We derive these equations in a usual fashion of a rotating
frame approximation under our initial conditions  and
and  ,
,
i.e. we consider the atom to be initially in the spin-down state until the applied field to be turned on.
The coefficients  are completely specifying the properties of this atom at any moment on the time interval
are completely specifying the properties of this atom at any moment on the time interval  before the pump field (1) to be turned off at any instant
before the pump field (1) to be turned off at any instant  . A time dependent behavior of these coefficients can be obtained from Eqs.5 as follows
. A time dependent behavior of these coefficients can be obtained from Eqs.5 as follows
|
|
(6) |
Here the general (dnonresonant) Rabi frequency is 
These functions can be used to find the average value of energy of the single atom after taking the mathematical expectation
|
|
(7) |
followed by inserting the wave function (2) and Hamiltonian  into it , making use of the stationary Schroedinger's equations
into it , making use of the stationary Schroedinger's equations
|
|
(8) |
and orthonomality of the eigenstates  .
.
As a result we obtain a time behavior of energy
|
|
(9) |
where the interaction Hamiltonian is represented through nondiagonal matrix elements of the dipole moment operator and the applied field as follows
|
|
(10) |
where one usually accept  and
and  .
.
Taking into account that  and substituting the Ex.(6) into (9), we can obtain time behavior of energy of the single atom during transition from the stationary state
and substituting the Ex.(6) into (9), we can obtain time behavior of energy of the single atom during transition from the stationary state  to a higher one
to a higher one
|
|
(11) |
where the parameter q(t) is a real time dependent periodic function
|
|
(12) |
As to the high-frequency oscillations of the energy (the second and third terms in q(t) ) , they are rather small to be neglected at all because usually  . Really, in experiments, the Rabi frequency is not more than 1010s-1 at the frequency of optical transition
. Really, in experiments, the Rabi frequency is not more than 1010s-1 at the frequency of optical transition  of about 1015s-1 . Therefore behavior of energy for the single atom during the spectroscopic transition is practically specified by the first term of to the q(t). As an example in F
ig.1 , we show this behavior for two different situations: at exact resonance (frequency of the pump field
of about 1015s-1 . Therefore behavior of energy for the single atom during the spectroscopic transition is practically specified by the first term of to the q(t). As an example in F
ig.1 , we show this behavior for two different situations: at exact resonance (frequency of the pump field  is equal to
is equal to  ) and at detuning from resonance (at
) and at detuning from resonance (at  ) .
) .

Fig.1. The dynamics of energy for the single atom during spectroscopic two-level transition between the stationary states E1 and E2 (two examples)
Ao - amplitude of step-like laser probe field, units ,
 - average value of energy (increase in
- average value of energy (increase in  units at time in
units at time in  ):
):
1- exact resonance (  )
)
2- detuning from resonance ( ) at
) at 
Three important conclusions can be deduced from the analysis of this Fig and the Exs.(11,12):
- changing of energy of the single atom during its spectroscopic transition from the initial state to the final one occurs step by step by deterministic way, i.e. without any sharp jumps at some time

- the spectrum of energy for all of superposition states
 lies in the interval between E1 and E2
lies in the interval between E1 and E2 - at availability of detuning from exact resonance ,average energy of atom can not possibly reach the upper level 2, i.e. in (11)
 . because the parameter q(t) is always less than unity due to
. because the parameter q(t) is always less than unity due to 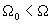
Thus, in the case of detuning from resonance , the energy portion which the atom takes away from the applied field at any instant of time is less of  , i.e. the photon energy. Logical conclusions follow from this: in this process the atom is no obliged to absorb an energy in the form of photons and the field is no obliged to give the energy in the form of photons. Both of these conclusions make doubt to the main principle of the quantum electrodynamics, namely to indivisibility of a photon. Moreover, if one to guess that indivisibility of a photon holds true we can arrive to once more contradiction concerning to the energy conservation law.
, i.e. the photon energy. Logical conclusions follow from this: in this process the atom is no obliged to absorb an energy in the form of photons and the field is no obliged to give the energy in the form of photons. Both of these conclusions make doubt to the main principle of the quantum electrodynamics, namely to indivisibility of a photon. Moreover, if one to guess that indivisibility of a photon holds true we can arrive to once more contradiction concerning to the energy conservation law.
Let us discuss that more in detail.
While the atom is proceeding from the spin-down state to the upper level its energy evolves deterministically, see Ex.(11). If the external field to be turned off at any time te the atom has to relax to the spin-down level, i.e. the atom should return the amount of energy that is less one photon energy.
This portion should be returned by means of electromagnetic radiation due to the induced dipole moment. Accordingly to quantum electrodynamics this field should consist of photons with energy  each. Thus having got the amount of energy less one photon the atom has to return an amount more one photon at least. This obviously contradicts to the main principle of nature, namely to conservation energy law.
each. Thus having got the amount of energy less one photon the atom has to return an amount more one photon at least. This obviously contradicts to the main principle of nature, namely to conservation energy law.
This same situation occurs at the exact resonance excitation ( ,
, ).In this case the atom may reach to the upper level only at the concrete instants
).In this case the atom may reach to the upper level only at the concrete instants
|
|
(13) |
Only for these moments we can guess the atom to has adsorbed one photon and the field has lost one photon as well. However to the other instants this conclusion does not hold true. For example, let us turn off the pumping field at the moment ,i.e. when the atom is in superposition state in which it has a concrete induced dipole moment oscillating with a frequency
,i.e. when the atom is in superposition state in which it has a concrete induced dipole moment oscillating with a frequency  and energy less than
and energy less than  .
.
Consequently, if to admit indivisibility of the photon a violation of energy conservation law could be available at exact resonant conditions as well.
Thus in order to the main principle of the nature does not is violated we must conclude that the coherent optical field is able to give his energy back in any amount by no means photons.
Such a conclusion could be reasonable at supposition that a monochromatic coherent wave is no consist of photons at all. In this case a great many misunderstandings can be removed by a natural way. As a matter of fact the monochromatic wave could be considered as a special phase state. Certainly, the optical field can be prepared by means of photons, as a water in a glass by drops. However both we can no assert the water in the glass consists of drops because there are no drops in the glass at all and we are not obliged to guess the monochromatic field consisting of photons. All depends on a preparation way of the field. For example, an incoherent field can be consistent of photons because they do not interfere each other. But the field prepared coherently, for instance by lasers, is in a new photonless phase state (water-like state) because in an active medium the induced radiation is co-ordinating reactions all of the dipoles in the volume.
- Allen L.,Eberly J.H. Optical resonance and two-level atoms, New York, Willey-Interscience Publication, 1975.
- Letokhov V.,Chebotaev V., Principles of nonlinear laser spectroscopy, Moscow, “Nauka”, 1975, in Russian.









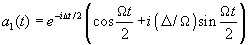








 , m=1,3,5...
, m=1,3,5...