Copyright ã E.Shtyrkov,April ,2005

E.I. Shtyrkov

Kazan Phys.-Technical Institute, Kazan, Russia

The device consists of a source of radiation (the satellite) and a receiver (antenna of a radio-telescope). The choosing of a geostationary satellite in the capacity of a source gives us in that case the zero relative uniform velocity for both the source and the receiver. The coordinates (geocentric longitude and latitude) of such a satellite remain practically same with respect to Earth’s frame during very long times. For this purposes we used the Intelsat704 satellite (USSPACECOM Catalog No.23461) with the geocentric East longitude of 66deg.E and the small inclination of 0.02deg. Diurnal observations were performed in Kazan (Russia) during three years (1997-2000) at different dates. To compare the experimental data obtained we computed the satellite’s position for a particular time of interest by means of an algorithm described in the Intelsat Earth Station Standards-IESS-412 (see Supplementary Method). Instead of computing all physical effects which act on a satellite, they describe the resulting sum of all these effects in terms of three equations with approximation containing 11 parameters obtained by means of the least-squares curve fitting. With the algorithm specified above this set of parameters will approximate the same satellite location as it is predicted by the original program. After generation of these ephemeris for the specified satellite and time period by Intelsat, we could always find the results on the site www.intelsat.com with a weekly renewal. Basing on the satellite’s predicted position and the known position of the Earth station, we calculated the geometric pointing angles (azimuth and elevation) via the Intelsat software program POINT40. Finally these pointing angles were corrected for the effects atmospheric refraction. We operated in a program track mode and undertook some specific measures since our earth station antenna position indicators and timing unit count scale have been corrected by producer during station's installation in order to remove the offsets resulting from mechanical and electronic drift in their calibration and/or anomalies of other origin. We supposed that at least a part of the anomalies observed within the tracking is due to motion of the Earth and therefore there were no reasons to remove them during corrections. Consequently, in our calculation we used the uncorrected station position measured by us with the GPS-38 navigator. In addition, in order to remove the corrections of time scale of telescope, we controlled the universal mean time (GMT) at every measurement independently.

Theory and experimental results

With the aim to determine parameters of Earth's motion in the space, we dwelt on the light aberration phenomenon during diurnal tracking of the geostationary satellite. Presently, the measurement of stellar aberration discovered by Bradley in 1728 became a routine operation in astronomy. Therefore we omit a detailed discussion of this phenomenon here (see, for example, the textbook [10]). The principal points are as follows:

• the telescope should be tilted slightly toward the direction of the Earth’s motion and this angle equals radians for stars located in a direction with the Earth orbital velocity , being the velocity of light in the vacuum,
• as established experimentally, no motion of stars has influence on the aberration angle and the velocity of light propagation,
• the aberration angle does not depend on a distance between a star and an observer. The above facts show that this phenomenon is of universal nature, being based on general conformities of natural laws for light propagation and motion of the observer in the space. Therefore we can deduce that an electromagnetic wave either emitted or scattered by any body (not solely by celestial objects) must be subject to an aberration with the angle depending only on the parameters of observer's motion. Consequently, one can assume that such an aberration may also occur within observing satellites. If this is the case, then observers (or devices) see not actual satellite positions calculated geometrically. They perceive apparent coordinates of a satellite, which depend strongly on the time since the aberrational angles change during a day and a year due to Earth’s rotation and its orbiting around the Sun.

To determine the time behavior of aberrational contributions into actual position of a satellite, we choose the equatorial plane in the rotating reference frame (the Earth) in order to consider a specific case when the satellite is situated in the Greenwich meridian plane with zero inclination of its orbit (on the X- axis in Fig.1).

Fig.1 Positions of the velocity vectors in the geo-centered rotating equatorial reference frame at the moment t after the start of a new tropical year.

Here, the orbital velocity vector V_orb is directed along the orbital components of the Earth motion. To specify the galactic velocity of the Sun’s system, we used the apex vector V_apx with the declination angle referenced to the equatorial plane and the right ascension measured counterclockwise with respect to the vernal equinoctial direction. In addition to Earth gravity, the satellites are subject to many forces (Sun, Moon, planets) which slightly perturb the orbits during a day. For geostationary satellites with a small inclination, the force of radiation pressure from the Sun is the main cause of diurnal small deviations of geocentric longitude and latitude with respect to the equilibrium point, which results in a small actual displacement of the satellite. The vector S specifying this force is considered here along with the velocity vectors in order to show the relation between the actual (geometric) and apparent (due to aberration) contributes to the satellite longitude and latitude.

At the initial position (autumnal equinox 00:00:00 GMT, 23 September), the X-axis is directed along the vernal equinoctial direction ( - point). At this time, the solar vector S has the same direction and is located in both the ecliptic and equatorial planes, while the vector V_orb , orthogonal to S at any time, is located in the YZ-plane and is inclined to Y-axis by the constant angle between the equatorial and ecliptic planes. In this left-hand frame (see Fig.1), both these vectors are rotating clockwise with the angular frequency of Earth rotation. Moreover, due to orbiting of the Earth around the Sun, their angles with Z-axis are slowly varying during a year. On the contrary, the angle between the vector V_apx  and the polar axis remains constant; however, the frequency of V_apx rotation is slightly higher in view of the orbiting of the Earth. This can be written as follows: , where , being the duration of the tropical year (365.2422 days for our epoch). Such time-dependent behavior of all these vectors result in changes of the geocentric longitude () and latitude () of the satellite during a day and a year.

1. The calculation shows that for a small disturbance of the actual positions due to light pressure we have

where are the amplitudes of Y,Z-components of the actual satellite displacement, stands for the radius of the satellite orbit, denotes an angle varying slowly during the year (Earth’s orbiting phase), is the amount of days taken from 00:00:00 GMT September, 23 (the start of the tropical year).

2. The aberration angles for the geo-centered observer as additions to the actual longitude and latitude (obtained after the geometrical calculating the projections of the vectors and  on Y-axis and Z-axis orthogonal to the source-observer line) are

where and

These additions were taken into account in the calculation of pointing angles: the azimuth and the elevation .

The astronomical azimuth observed at tracking satellite can be written as the sum of the actual term calculated geometrically and the respective contributions if we expand this function in Taylor series and neglect the terms above first-order one (as usually, ):

where , , and ,

The first term in Eq.(3) can be found by means of a routine operation usual in the celestial mechanics for transition from the equatorial frame to horizontal one aligned with the Earth station meridian. We simply cite it here without deriving

where , and are the geodetic longitude and latitude of a specific Earth station (the telescope) . This function will be used later for obtaining the derivatives in Eq.(3).

The calculation of the first term by POINT40 program with using 11 parameter ephemeris information and real coordinates of our Earth station (geodetic longitude of 55.765 deg.E , latitude of 49.228 deg.N and height above IAU-1976 Earth ellipsoid, adopted by Intelsat as the reference, of 0.13 km) shows that the calculated geodetic () actual azimuth oscillates as in phase with the variation of S direction, see Eq.(1). It can be clearly seen in Fig.2, where the example of such a 3-day behavior both the actual (predicted-lower plot) and apparent one (observed-above) is shown in the local mean time frame (LMT in hours). The maximum values for the azimuth are achieved at a time about 6 hours (on sunrise), when the light pressure force is orthogonal to the line of observation and the East longitude of the satellite reaches its minimum.

Fig.2 The observed (upper plot) and predicted (lower) geodetic azimuth for Intelsat704 satellite during September, 27-30, 1997.

Taking into account the offset of azimuth due to mechanical and electronic drifting in the calibration of azimuth, we can rewrite Eq.(3) as follows

where the coefficients , are the first-order derivatives of Eq.(4) with respect to and 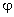, here being the offset. The last term is almost constant and together with the previous one (being also a very slowly varying function) gives us a pedestal for the azimuth observed.

Firstly, in Eq.(5) we consider only the two terms (the second and third ones) oscillating with the frequency of Earth's rotation. By using the contributions Eq.(2) and Eq.(5), we obtain for the oscillating terms

where and is the ratio of projection of V_apx on the equatorial plane to the free space velocity of light. Following simple trigonometric transformations, the latter yields

where both the amplitude and the phase of the observed curve obey the relation

for .

From Eq.(7) we derive that the experimental oscillating plot for later times should be shifted relatively the actual one by the angle . Such a phase shift was really observed in all our measurements. One can see this behavior, for example, in Fig. 2, where the experimental plot is delayed on 40 min () . This shift is more clearly seen in Supplementary fig.4 where the plot is depicted in polar coordinates.

The equation (8) is the principle point of this paper, since along with the experimental data (and ) measured at different dates and Eqs.2 it allows us to find the orbital and galactic velocities, apex of the solar system and afterwards compare them with the values of the Earth orbital velocity and the apex right ascension of the Sun system, well-known in the astronomy.

We determined these parameters by the treatment of experimental data accumulated for a long period of time (1998 - 1999). The calculations of , and were performed numerically (with Mathcad7) by solving of the set of three Eqs.8 taken for three distinct dates. Some examples of such a solving are presented in Supplementary Equations1. The days were chosen so that the Earth orbital velocities could be equal as far as possible at these days of year. The calculations were performed with the following parameters:

the geodetic latitude and the longitude of the telescope,

the angle between ecliptic and celestial poles is , the duration of the tropical year (our epoch) , being the amount of days from the start of the new tropical year ( 00:00:00 GMT, September, 23) up to the specified date. In Fig.3 we present the results obtained for the orbital velocity of the Earth ( ) at different days during more than 1.5 years.

Fig.3. Behavior of the orbital velocity of the Earth during the period March1998- December1999

Each point here for the specified date is the result of an averaging over the set of equations (8) where this date is used. From the plots one can easily see that the behavior of the orbital velocity of Earth obtained in this experiment is similar to the one accepted in the observational astronomy:

• their average annual values practically coincide (29.45 km/s in this experiment and 29.765 km/s in the astronomy)

• the velocities are slightly higher at the winter solstice (the perihelion of Earth's orbit) and slightly lower at summer (the Earth passes through the aphelion) if compared with the equinox days.

From this coincidence of velocities one can conclude that the complete aberration takes place, i.e., the aberration angle for satellites is as well as for any star .

As for the apex right ascension obtained in this experiment, its value is close to 269.99^o for the solution of every set of Eq.8. This almost coincides with the hour angle of Sun apex equal to 18^h59 ^min, i.e. 269,75^o accepted in the astronomic sources. In the geometry of our experiment, the projection of the galactic velocity vector onto the equatorial plane turned out to be very small - average annual value of ( close to 5km/s ). The small value of this component for rather large expected Sun velocity could be explained if the apex declination is higher than the generally accepted meaning (51^o30’ close to - Draconis). To evaluate the declination of the apex and the velocity of galactic motion of the solar system we used the ratio . The experimental value was obtained from the relation

where are the first- and second-order derivatives of the actual elevation with respect to the latitude of satellite, being the constant difference between the actual and observed elevations, while is the refraction correction at our elevation . In view of rather cumbersome intermediate calculations, Eq.(9) is given here without deriving. To derive it one needs the following steps. First, one should use POINT40 to calculate the predicted elevation and compare it with the observed one to obtain pedestal (see Supplementary fig5). Afterwards, in the expression for elevation, obtained as (3) by expanding in Taylor series and keeping the second derivative with respect to latitude (see Supplementary Equations2), one takes all terms independent of time and put them equal to . By solving the quadratic equation obtained we arrive to Eq.(9).

By using in Eq.(9) the average annual experimental value of we thus obtain the aberrational angle caused by the galactic motion. This gives us the respective estimates for the apex declination and, after applying the last term in Eq.(2), the upper limit for the solar system velocity of approximately 600 km/s.

Conclusion

The results obtained in this experiment make it possible to conclude that the velocity of a uniformly moving laboratory system (the Earth) can really be measured with the device with a source of radiation and a receiver fixed with respect to each other and the system itself.

The latter means that the uniform motion of the laboratory must possess an influence on the results of experiments performed in this laboratory with the use of physical electromagnetic phenomena.

Acknowledgments

Author would like to express the sincere gratitude to the member of TAT-01B Earth station's staff in Kazan, Mr. O.Vybornov who kindly agreed to provide the information about the current positions of Intelsat704 satellite. His valuable assistance in 1997-2000 certainly contributed to the success of the experiment.

References

1. A.A. Michelson. The Relative Motion of the Earth and the Luminiferous Ether.The American Journal of Science, Third Series. 22, 120 (1887).

2. A.A. Michelson, E.W. Morley. On the Relative Motion of the Earth and the Luminiferous Ether. The American Journal of Science, Third Series. 34, 333 (1887).

3. D.C. Miller. Significance of the ether-drift experiments of 1925 at Mount Wilson. Science 63, 433 (1926).

4. A. Michelson, F. Pease, F. Pearson. Repetition of the Michelson-Morley experiment. JOSA 18, 3, 181 (March 1929).

5. R.J. Kennedy. A of the Michelson-Morley experiment. Proc.Nat.Acad.Sci. 12, 621 (1926).

6. A.Piccard, E.Stahel. Das Michelson-experiment, ausgefuhlt auf dem Rigi. Comptes Rendus 183, 420 (1926).

7. K.Illingworth. Repetition of the Michelson-Morley experiment using Kennedy’s refinement.Physical Review 30, 692 (1927).

8. J.P. Cedarholm, C.H.Townes. A new experimental test of special relativity. Nature, 184, №4696, 1350 (1959).

9. Conference on Michelson-Morley experiment. The Astrophys.J. 68, 5, 341 (1928)

10. R. Feynman, R.Leighton, M.Sands. The Feynman Lectures of Physics, 1, (Addison-Welsey, New York, 1963).

Loading this paper in PDF-format