Эфирогидродинамика как преемница электро и гидродинамики

УРАВНЕНИЕ МАКСВЕЛЛА ДЛЯ ЭФИРОГИДРОДИНАМИКИ ОПИСЫВАЕТ, В ЧАСТНОСТИ, И ПРОЦЕСС РОЖДЕНИЯ И ЭВОЛЮЦИИ СПИРАЛЬНЫХ ГАЛАКТИК

Пруссов П.Д.

В развитие работы [1] , вобравшей в себя опыт развития теории эфира (монографии [2] и [3] ) в объяснении явлений природы как освобождении от пут эйнштейнианства (пытающегося удерживать науку в качестве заложницы в своих будто бы безэфирных кельях “специальной” и “общей” ), покажем, как первое уравнение Максвелла, считавшееся прежде приобретением лишь электродинамики, дает возможность в эфирогидродинамике как преемнице электродинамики и гидродинамики решить важнейшую вековую проблему зарождения и эволюции галактик. Словесное описание этой проблемы впервые было дано в [3]. Развивающаяся эфирогидродинамика выводит теорию и на математическое описание проблемы.

Пусть скорость смещения цилиндрических слоев относительно друг друга в струе (т.е. - относительная скорость ) возрастает с удалением ее от оси по радиусу r ее поперечного сечения по закону

(1)

где - относительная скорость на оси струи, k – коэффициент пропорциональности. Тогда напряжение вязких сил (с учетом их поперечности струе [4]) равно

, (2)

где n - коэффициент динамической вязкости.

Теперь становится очевидным, что в [4] еще не все сказано об ошибочности формулы Ньютона для коэффициента вязкости: в ней выражение grad для берется со знаком “минус”, поскольку – де речь идет о силе сопротивления (это сказалось и в работе [1] ). Но наличие знака “минус” здесь свойственно лишь потенциальным силам, а силы сопротивления таковыми не являются. Кроме того, при этом напряжение вязкости оказывается убывающим при удалении от оси.

Поперечность вихря, создаваемого вязкими силами на струе, аналогична поперечности магнитного и электрического полей в электродинамике, в том числе и в уравнениях Максвелла.

Струю, возникшую вследствие флуктуации скорости частиц сферы и становящуюся исходным этапом зарождения галактики [3], будем характеризовать величиной , где - плотность среды в потоке струи, - скорость этого потока, т.е. плотность количества движения в струе. Кстати, размерность [ ] = г/(см²с) является и размерностью напряженности E электрического поля (и магнитного поля Н) в натуральной системе единиц [3].

В уравнении Максвелла для гидродинамики возьмем производную от по времени в виде , поскольку при отсутствии зарядов увлечение среды незначительно, и мы им пренебрегаем.

Заметим, что в первом уравнении Максвелла в электродинамике в качестве фактора завихрения используется операция , с помощью которой величиной фактически описывается завихрение эфира шлейфом из эпсилино вытягивающимся за движущимся зарядом, благодаря вращению эфирных вихревых торов, из которых набраны эпсилино, чем обеспечивается поперечность электрического и магнитного полей. (С этого начиналось построение эфирных моделей в электродинамике (конец 1948), но первые публикации моделей стали возможны лишь с выходом первой части монографии [2] (1992)).

В гидродинамике заряды отсутствуют. Здесь завихривающим фактором служит вязкость, напряжение которой, поперечное струе, будем дифференцировать в уравнении Максвелла для гидромеханики по пространственной координате , считаю, струю направленной по оси Ox, так что (беря абсолютные значения векторных величин):

- (3)

- первое уравнение Максвелла для гидродинамики. По внешнему виду оно несколько отличается от соответствующего уравнения Максвелла в электродинамике при отсутствии зарядов:

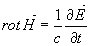, (4)

но физическая суть уравнений (3) и (4) едина – линейный поток в среде сопровождается вихрем вокруг него, что описано при вводе уравнений Максвелла в [3]. (В данной работе используется система единиц СГС, которая по общему мнению незаменима в теоретических исследованиях, почему и допускается наряду с СИ).

Приступая к описанию стадий эволюции галактики вплоть до спиральной, учтем, что при сверхзвуковой скорости струи v струя сама для себя создает преграду из уплотняющейся перед нею среды, наталкиваясь на которую, струя тормозится. В результате плотность в струе нарастает:

(5)

где - плотность среды в струе при , - коэффициент пропорциональности, а скорость струи v уменьшается:

(6)

где - скорость струи при , - коэффициент пропорциональности.

Учтем также, что скорость убывает и вследствие внутреннего трения в среде, при этом она становится функцией и радиуса поперечного сечения струи, так что по (1)

где выполняет роль относительной скорости при ,

или по (6) :

, (7)

По (5) и (7) величина приобретает вид :

, (8)

При подстановке (7) и (8) в (3) учтем, что для данного слоя с радиусом в струе, для которого записано уравнение (3) , . Так как , то в результате подстановки имеем:

где , так что после сокращения на получаем :

откуда ,

а в результате логарифмирования при

, (9)

где при радиус , т.е. формула (9) описывает логарифмическую спираль, в которую и превращается зрелая спиральная галактика.

ЛИТЕРАТУРА

Пруссов П.Д. Эфирогидродинамика как преемница электро – и гидродинамики. / Журнал “Эниология”.

Пруссов П.Д. Явление эфира. 4 части. Николаев, 1992 – 1998.

Пруссов П.Д. Физика эфира. Николаев: Приват – Полиграфия, 2003, 286с.

Пруссов П.Д. Считая силу сопротивления в формуле Ньютона для коэффициента вязкости продольной, что справедливо для лобового сопротивления, а не поперечной, как должно быть для вязкого трения, физики так и не научились описывать причину появления вихрей. / Серия “Проблемы исследования Вселенной”, вып. 24, 2002, С. – Петербург.

к оглавлению