к оглавлению

Великая теорема Ферма

Валерий ПЕТРОВ

В статье Владимира Латышева Саймон Флэгг и дьявол, рассказывается о том, как ученый-математик Саймон Флэгг и дьявол заключают традиционный договор о продаже души с условием, что последний за 24 часа ответит на один-единственный вопрос: “Верна ли великая теорема Ферма?” В действительности, однако, все было не так.

Более 350 лет математики всего мира безуспешно ищут ответ на вопрос: “Верна ли великая теорема Ферма?”. Не находит его и дьявол, изучив за 10 часов все без исключения разделы математики и потратив остаток времени на собственные изыскания, он, за 10 минут до истечения срока, появляется с пачкой исписанных листков, швыряет их на пол и топчет ногами. И, признав свое поражение, исчезает… Однако спустя несколько минут появляется вновь и вместе с человеком начинает искать ответ на поставленный вопрос”.

В действительности, однако, все было несколько иначе. Когда дьявол узнал об условии заключения договора с ученым-математиком о продажи его души, он рассмеялся и сказал: “Нет ничего проще. У меня есть доказательство этой теоремы, написанное самим Ферма”. С этими словами дьявол достал из кармана аккуратно сложенный лист бумаги и протянул его ученому. Флэгг уселся поудобнее в кресло у камина и стал читать.

“Пусть имеется три целых числа, удовлетворяющих уравнению:

zn = xn + yn (1).

Известно, что три числа, удовлетворяющих уравнению (1), должны удовлетворять следующим условиям:

одно из чисел, например, z, должно быть четным, два других - нечетными;

числа должны быть взаимно простыми, т.е. попарно не должны иметь общих множителей;

никакие два числа не могут быть равны друг другу.

Предположим для определенности, что z > x > y.

Очевидно, что число z меньше суммы двух других чисел, т.е.

z < x + y (2).

Пусть имеется три отрезка длиной z, x, y, удовлетворяющих условию (2). Тогда в силу известной теоремы на этих отрезках можно построить треугольник как на сторонах. Известно, что треугольник, между сторонами которого имеет место соотношение (1), при n > 2 остроугольный.

Тогда для сторон этого треугольника имеет место соотношение, вытекающее из теоремы косинусов:

z2 = x2 + y2 – 2xycosα :

где α – угол между сторонами x и y.

Построим остроугольный треугольник ABC со сторонами AB = x, BC = y, AC = z. Опустим из точки A остроугольного треугольника ABC перпендикуляр на противолежащую сторону BC, как это изображено на рисунке.

Рис. 1. Остроугольный треугольник

Из треугольника BC1C находим cosα = m1 / BC = m1 / y. Подставляя значение cosα в (2), получим:

z2 = x2 + y2 – 2xym1 / y

z2 = x2 + y2 – 2xm1 (3)

Таким образом, для одного и того же треугольника одновременно имеем два различных соотношения между его сторонами: (1) и (3). Тогда суть теоремы может быть выражена иначе: Требуется доказать, что никакие целочисленные решения уравнения (3) не являются таковыми для уравнения (1).

Умножим уравнение (3) на zn-2. Получим:

zn-2z2 = zn-2x2 + zn-2y2 – 2xzn-2m1 (4)

Пусть zn-2 = xn-2 + a = yn-2 + b, где a и b – некоторые целые числа, обеспечивающие указанные равенства. Тогда, подставляя значение zn-2 в (4), получим:

zn = (xn-2 + a) x2 + (yn-2 + b) y2 – 2x(xn-2 + a)m1

zn = xn + ax2 + yn + by2 – 2x(xn-2 + a)m1 (5)

Вычитая (1) из (5), получим:

0 = ax2 + by2 – 2x(xn-2 + a)m1 (6)

Таким образом, если при каких-либо целочисленных значениях чисел x и y уравнение (6) окажется равным нулю, то решение этого уравнения (т.е. значения чисел x и y) будет одновременно решением уравнения (3).

Решая данное уравнение, получим:

by2 = 2x(xn-2 + a)m1 - ax2

by2 = x[2(xn-2 + a)m1 – ax]

Запишем для простоты вычислений 2(xn-2 + a)m1 – ax = k. Получим:

by2 = kx,

откуда следует:

,

 

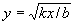т.е. 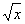является одним из множителей числа y.

Таким образом, целочисленные решения уравнения (6) оказываются возможными только при условии, что 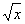является одним из множителей числа y, что противоречит начальным условиям задачи. Следовательно, ни при каких значениях чисел x и y, удовлетворяющих начальным условиям задачи, уравнение (6) не имеет целочисленных решений. Следовательно, ни при каких значениях чисел x и y, удовлетворяющих начальным условиям задачи, уравнение (6) не может быть равным уравнению (1). Следовательно, ни при каких значениях чисел x и y, удовлетворяющих начальным условиям задачи, уравнение (1) не может иметь каких-либо целочисленных решений. Это значит, что в остроугольном треугольнике, между сторонами которого имеет место соотношение (1), по крайней мере, одна из сторон не может быть выражена никаким целым числом. Что и требовалось доказать.

Флэгг задумался на мгновенье и неожиданно швырнул бумагу прямо в огонь. “Зачем Вы это сделали?” – воскликнул дьявол. “Я нахожу, что слишком дешево продал свою душу. Так пусть же никто больше не воспользуется этим доказательством!” – ответил Флэгг.

“В самом деле”, подумал дьявол, “пусть математики еще поломают головы над доказательством этой теоремы”.
к оглавлению