Об увлечении эфира движущимися средами:
от Френеля до Эйнштейна
Аннотация:
В статье обобщаются результаты исследования опыта Араго и теории Френеля, предложенной специально для объяснения результатов этого опыта. Показывается, что вывод Араго о независимости коэффициента преломления линзы от состояния её движения относительно внешнего источника света не соответствуют действительности. Обосновывается вывод, что теория Френеля, основанная на ошибочных результатах опыта Араго, не может быть истинной. Следовательно, не могут быть истинными и опыты, подтверждающие истинность ошибочной теории.
ВВЕДЕНИЕ
Современная наука не отрицает истинности Френелевской формулы частичного увлечения эфира движущимися телами (средами) - "... и сейчас одного из наиболее важных явлений в движущихся телах" [1]. В современной теории относительности формула Френеля рассматривается как частный случай более общей "релятивистской" формулы сложения скоростей.
Любая научная теория может считаться истинной, если она удовлетворяет, по крайней мере, следующим критериям:
основана на предположениях, соответствующих физической действительности;
является внутренне логически непротиворечивой;
предсказываемые теорией явления наблюдаются в действительности.
Как полагают, формула Френеля основана на вполне достоверных данных опытов Араго и подтверждается опытами Физо. Однако исследование как опытов Араго, так и других известных опытов и явлений, не дают оснований считать общепринятое мнение соответствующим действительности.
ОПЫТ АРАГО
В 1801 г. Араго выполнил опыт, цель которого заключалась в проверке выдвинутого Мичелом предположения, что движение призмы или линзы должно сопровождаться изменением ее коэффициента преломления. Суть рассуждений Мичела заключалась в том, что при полностью неувлекаемом веществом линзы (или призмы) эфире скорость света внутри линзы будет равна
c/n + v при движении линзы в одном направлении и c/n - v при движении линзы в противоположном направлении, где v – скорость движения линзы относительно эфира, n – коэффициент преломления вещества линзы.В первом случае, при движении навстречу лучу света, коэффициент преломления
n1 будет равенn1 = (c/n + v) / c = n + v / c. (1)
Во втором случае, при движении линзы в обратном направлении, коэффициент преломления
n2 будет равенn2 = (c/n - v) / c = n - v / c. (2)
В своих опытах Араго использовал свет от одной из звезд. Вследствие движения Земли относительно этой звезды, скорость света в призме будет равна
c/n + v при движении Земли в одном направлении относительно излучаемого звездой света, и c/n – v при движении Земли в противоположном направлении. Соответственно должен изменяться и коэффициент преломления призмы Однако Араго не обнаружил никакого эффекта, обусловленного движением призмы вместе с Землей относительно звезды, и пришел к выводу, что движение призмы вместе с Землей “... на показатель преломления не влияет. Это заключение правильно, действительно не влияет”, соглашается с ним Л.И.Мандельштам в [1]. В действительности, это не так. Известно, что движение приемника света, в данном случае - линзы, относительно источника света сопровождается, как это установил Доплер, изменением частоты света, принимаемого приемником. Коэффициент преломления линзы, в свою очередь, зависит от частоты света: “... факт зависимости показателя преломления от частоты света называется дисперсией, так как именно из-за дисперсии свет раскладывается призмой в спектр” [2].Таким образом, коэффициент преломления линзы зависит
от состояния ее движения относительно источника света. Опыты Араго оказались недостаточно точными. Однако во времена Араго эффект Доплера еще не был известен, вследствие чего Араго счел результаты своих опытов вполне достоверными. Результаты опытов Араго можно было объяснить полным увлечением эфира веществом линзы. В этом случае скорость движения эфира внутри движущейся призмы оказывается равной нулю, вследствие чего коэффициент преломления остается величиной постоянной, независимо от скорости движения призмы, однако как объяснить само полное увлечение Араго не знал и обратился за разъяснениями к Френелю. Френель, не подвергая результаты опытов Араго ни малейшему сомнению, предложил гипотезу, согласно которой эфир увлекается движущимися телами не полностью, а частично, вследствие чего скорость “эфирного ветра” внутри движущегося тела (или среды) оказывается равнойvс = v(1 - 1/n2),
где v - скорость движения тела (среды) относительно внешнего по отношению к этому телу (среде) эфиру; n - коэффициент преломления вещества движущегося тела или среды.
Каким же образом гипотеза Френеля объясняет результаты опытов Араго? Пусть n2 = 2. Тогда частичное, по Френелю, увлечение эфира внутри движущейся линзы может уменьшить в 2 раза эффект, обусловленный ее движением, тогда как требуется полностью его исключить. Очевидно, суть дела заключается не в частичном увлечении эфира движущейся линзой, а в том, что линза в опыте Араго находится внутри атмосферы Земли, коэффициент преломления которой можно считать равным 1. Тогда частичное, по Френелю, увлечение эфира применительно к атмосфере означает полное его увлечение, так как при n = 1 скорость “эфирного ветра” в атмосфере Земли оказывается равной нулю – “эфирный ветер”, обусловленный движением Земли, в атмосфере Земли не возникает, а потому не может возникнуть и в призме, погруженной в атмосферу.
Как считает У.И.Франкфурт, в теории Френеля “Все происходит так, как будто эфир внутри (здесь и далее подчеркнуто мной - В.П.) тела движется относительно внешнего эфира со скоростью v(1 - 1/n2), т.е. медленнее, чем само тело. Частичное увлечение эфира Френель понимал в том смысле, что движущееся тело увлекает не весь содержащийся в нем эфир, а только ту часть, которая соответствует превышению плотности эфира в теле над его плотностью в окружающей среде. В ...теории Френеля можно выделить следующие основные положения: 1) внешний эфир совершенно не увлекается неподвижными телами; 2) внутренний эфир почти не увлекается непрозрачными телами; 3) внутренний эфир частично увлекается прозрачными телами” [3].
Возникает вопрос: относительно какого наблюдателя эфир внутри движущегося тела (среды) движется со скоростью vс = v(1 - 1/n2)? В опыте Араго наблюдатель (сам Араго) неподвижен относительно призмы и движется вместе с ней относительно звезды с той же скоростью v, что и призма.
При полном неувлечении эфира веществом призмы скорость движения эфира внутри призмы равна скорости её (призмы) движения относительно эфира.
При полном увлечении эфира скорость движения эфира внутри призмы равна нулю; соответственно, эта скорость равна нулю и по отношению к наблюдателю, неподвижному относительно призмы и движущемуся вместе с ней.
При частичном увлечении эфира неувлекаемая его часть движется внутри призмы со скоростью v в направлении, обратном действительному движению призмы относительно эфира, тогда как увлекаемая часть эфира движется со скоростью v / n2 в том же направлении, в каком движется призма. Поэтому относительно наблюдателя, движущегося вместе с призмой, как это было в опыте Араго, скорость движения эфира внутри призмы есть разность двух величин v и v / n2, так как скорости движения увлекаемой и неувлекаемой части эфира направлены противоположно друг другу:
v - v / n2 = = v(1 - 1/n2).
Чтобы лучше понять суть гипотезы Френеля, представим себе наблюдателя, находящегося внутри трубы, движущейся со скоростью
v относительно, скажем, неподвижного воздуха.Если труба открыта с обоих её концов, скорость движения воздуха относительно наблюдателя, находящегося внутри трубы и движущегося вместе с ней, равна скорости движения самой трубы, в направлении, обратном движению трубы. Это случай полного неувлечения воздуха внутри движущейся трубы.
Если труба закрыта с обоих её концов, скорость движения воздуха внутри трубы относительно того же наблюдателя равна нулю – это случай полного увлечения движущейся трубой воздуха, находящегося внутри трубы.
Наконец, представим себе, что труба закрыта с двух её концов не полностью, а частично, вследствие чего внутри трубы возникает движение воздуха, обусловленное движением трубы относительно воздуха. Это движение воздуха внутри трубы можно рассматривать как движение в двух противоположных направлений: со скоростью
v в направлении, обратном движению относительно окружающего её воздуха, и со скоростью v / n2 в направлении движения трубы вследствие частичного увлечения воздуха внутри движущейся трубы (в данном случае n есть некоторый коэффициент увлечения воздуха внутри движущейся трубы).С точки зрения внешнего наблюдателя, относительно которого труба движется с некоторой скоростью
v, движение воздуха в трубе выглядит иначе.Когда оба конца трубы открыты, воздух в ней не увлекается движением трубы, т.е. относительно внешнего наблюдателя остается неподвижным, как и вне трубы. Это полное неувлечение воздуха движущейся трубой.
При полностью закрытой с двух её концов трубе, воздух внутри неё движется относительно внешнего наблюдателя с той же скоростью, что и труба. Это полное увлечение воздуха внутри движущейся трубы.
Наконец, при частично открытой трубе относительно внешнего наблюдателя движется только увлекаемая трубой часть воздуха. Скорость этой увлекаемой части относительно внешнего наблюдателя будет равна
v / n2.Точно так же, согласно Френелю, выглядит и движение эфира внутри движущейся среды относительно внешнего наблюдателя, неподвижного относительно эфира:
при полном неувлечении эфира внутри движущейся среды скорость движения эфира относительно внешнего наблюдателя будет равна нулю – эфир остается неподвижным и внутри, и вне движущейся среды;
при полном увлечении эфира внутри движущейся среды скорость его движения относительно внешнего наблюдателя будет равна скорости движения
v самой среды;при частичном увлечении эфир внутри движущейся среды относительно внешнего наблюдателя движется со скоростью
v / n2 в направлении движения среды, так как с этой скоростью движется увлекаемая часть эфира.Мы должны будем вспомнить об этом при анализе результатов опыта Физо, выполненного с целью проверки гипотезы Френеля для движущейся воды.
Опыт Физо
Схема опыта Физо приведена на рис.1.
Жидкость (вода в данном случае) течет в изогнутой трубке со скоростью 
Второй луч (изображен синей линией) отражается от зеркала 2 и движется в том же направлении, что и вода в трубке. Отражаясь затем от системы зеркал 3 и 4, этот луч света также попадает на экран. В результате на экране возникает интерференционная
картина из чередующихся светлых и темных полос. Измерив их ширину, можно определить скорость движения лучей света в движущейся воде, тем самым - и степень увлечения эфира движущейся водой. Ширина интерференционных полос зависит от разности времен хода каждого из лучей света в движущейся воде. Согласно Физо, время движения одного из лучей света равноT1 =2L/(c/n + kv)
время движения другого луча равно
T2 =2L/(c/n - kv),
где 2
L - путь, который проходит луч света в движущейся воде; n - коэффициент преломления воды; k - Френелевский коэффициент увлечения эфира движущейся водой; v - скорость движения воды в трубке.Тогда разность времен хода лучей будет равна:
T2 - T1 = 2L/(c/n - kv) - 2L/(c/n + kv) = 4Lkvn2/c2(1 - k2v2n2/c2).
Пренебрегая величиной
k2 v2 n2 /c2 вследствие ее малости, получим:T2 - T1 = 4Lkvn2/c2
или в длинах волн:
= сc
, где сc = c / n – скорость света в неподвижной воде.
Таким образом, для лучей света, движущихся в воде, получим:
= 
= 
Тогда для отношения
получим:
, (3)
где
- длина волны света в воде.
Величину
найдем из следующих соображений:
в воздухе длина волны света
равна cT, где T – период колебаний волны;
в воде длина волны света
= cT/n, откуда следует: = /n.
Подставляя полученное значение
в (3), получим:
= 
(2).
Параметры установки в опыте Физо были следующими [3]:
Длина стеклянных трубок
L = 1,4875 м;Скорость протекания воды в трубках
v = 7,059 м/с;Показатель преломления света в воде
n = 1,333;Длина волны света в воздухе
= 0,536
10-6 м;
Скорость света в воздухе
c = 3108 м/с.
При данных параметрах величина
= 
0,473
Как известно, Физо полагал
k = (1 – 1/n2) = (1 – 1/1,3332 = 0,43721860,44.
Таким образом, данные расчета величины
нужно умножить на 0,44. Тогда для опыта Физо получим 
= 0,473 0,44 0,20809. Из опыта Физо получил величину 
= 0,230016, что соответствует k = 0,46. Несовпадение теории с экспериментом (0,230016 – 0,208097) / 0,208097= 0,10533 или 10,533%. Таким образом, результаты опыта Араго как будто подтверждают формулу Френеля. В действительности, это не так.
Как было показано выше, скорость движения эфира, увлекаемого движущейся средой, относительно неподвижного наблюдателя, равна
v / n2, а не v(1 - v / n2) как считал Физо. В опыте Физо неподвижный наблюдатель – экран, на котором появляются интерференционные полосы - находится вне жидкости, движущейся в трубке. Следовательно, скорость движения эфира в трубке, обусловленная движением воды, относительно этого экрана равна v/n2 . Тогда коэффициент увлечения эфира должен быть равен 1/n2 , а не 1 - 1/n2, как полагал Физо. При n = 1,33 получим k = 0,56, что не соответствует полученным Физо результатам.При полностью неувлекаемом движением воды эфире время
T1 будет равно T2 = 2Ln/c, поэтому разность времен хода лучей будет равна нулю. Очевидно, это не соответствует результатам эксперимента Физо.При полностью увлекаемом движущейся водой эфире, т.е. при
k = 1 время T1 будет равно T1 =2L/(c/n + v). Соответственно, время T2 =2L/(c/n - v). Тогда разность времен T2 и T1 будет равна:
T2 - T1 = 2L/(c/n - v) - 2L/(c/n +kv) = 4Lv/( c2/n2 – v2) = 4Lvn2 / [c2(1 - v2/ c2n2)].
Пренебрегая величиной
v2/ c2n2 вследствие её малости, получим T2 - T1 = 4Lvn2 / c2, что не соответствует фактически полученным Физо результатам. Таким образом, результаты опыта Физо не подтверждают Френелевскую формулу сложения скоростей, так как в этом опыте коэффициент увлечения по отношению к неподвижному экрану должен быть равен 1 / n2, а не (1 - 1 / n2). Вместе с тем, результаты этого опыта не соответствуют ни полному неувлечению эфира внутри движущейся жидкости (k = 0), ни полному его увлечению (k = 1). Так что же обнаружил Физо в своем опыте?Известно, что скорость движения воды в трубе изменяется в поперечном сечении в направлении от стенок трубы к её центру (оси симметрии). Это изменение скорости движения описывается формулой:
v = Δp(R2 – r 2) / 4ηl,
где Δ
p – распределение давления в жидкости, соответствующее распределению скоростей её движения; R – внутренний радиус трубы; r – радиус кольца жидкости в направлении от оси симметрии трубы к её стенкам; η – вязкость жидкости, движущейся в трубе; l – путь, который проходит жидкость в данной трубе.Согласно этому уравнению, скорость жидкости распределена по сечению трубы по параболическому закону. При
r = R, т.е. у стенок трубы равна нулю; при r = нулю, т.е. в центре трубы, скорость течения жидкости равна v. Надо полагать, что распределение скорости движения жидкости в поперечном сечении трубы должно сопровождаться соответствующим изменением длины волны также в поперечном сечении. Изменение длины волны должно вносить дополнительные искажения в наблюдаемую картину интерференции, однако ни в отчете самого Физо, ни в более поздних работах об этом опыте ничего не говорится о том, каким образом Физо учитывал распределение скорости движения жидкости в поперечном сечении.Настораживает также и то, что в своем опыте Физо удалось измерить скорость течения воды в трубке с точностью до 1 см/с, тогда как в аналогичном опыте Зеемана, выполненном спустя 63 года после опыта Физо, скорость движения среды, в которой распространялся свет, удалось измерить с точность до 1 м/с. Каким образом Физо удалось добиться столь высокой точности измерения скорости движения воды в трубке? Сам Физо ничего не говорит об этом. Таким образом, имеются достаточные основания сомневаться в истинности полученных Физо результатов, учитывая также и то обстоятельство, что сама гипотеза Френеля основана на ошибочных результатах опыта Араго, а поэтому не может быть правильной, следовательно, не может быть правильным любой опыт, доказывающий истинность неправильной гипотезы.
Продолжением описанного выше опыта Физо явился его опыт 1859 г. Установив, как он полагал, “... справедливость теории частичного увлечения для жидких и газообразных сред, Физо решил проверить ее для твердых тел. Для этой цели он использовал явление поворота плоскости поляризации при преломлении поляризованного света на границе двух сред. Угол поворота зависит от показателя преломления среды, а последний - от скорости света в данной среде. По мнению Физо, изменение ориентации прибора относительно направления поступательного движения
Земли должно было изменить относительную скорость света в среде. Проанализировав результаты 2000 опытов, Физо в 1859 г. объявил о подтверждении формулы Френеля и о наличии влияния движения Земли на поворот плоскости поляризации” [3]. Сама постановка этого опыта свидетельствует о непонимании Физо сути теории Френеля, согласно которой “эфирный ветер”, обусловленный движением Земли, в атмосфере Земли не возникает, а потому не может быть обнаружен никакими опытами. “Никто не мог обнаружить ошибку в этих опытах, а трудность их постановки была столь велика, что только через 43 года они были повторены и дали отрицательный результат” [3]. Надо полагать, что “отрицательный результат” означает, что опыт Физо 1859 г. не подтверждает формулу Френеля для твердых тел. Однако главная ошибка Физо, свидетельствующая о непонимании им сути теории Френеля, так и осталась незамеченной вплоть до настоящего времени.В опыте Физо 1851 г. жидкость в трубке движется относительно неподвижного источника света. Такой же результат может быть получен, если жидкость в трубке будет неподвижной, а вся установка будет двигаться относительно источника света с некоторой скоростью. Это дает возможность, используя некоторый внешний источник света (например, какую-либо звезду) определить скорость движения установки относительно этого источника. Идею такого опыта осуществил Хук в 1876 г. Схема этого опыта, как он описан в [4], приведена на рис.2.
Луч света попадает на полупрозрачное зеркало, где расщепляется на два луча, один из которых движется против направления движения прибора (изображен черным цветом), другой – в том же направлении (изображен синим цветом). Прибор движется вместе с Землей относительно некоторой звезды со скоростью 
Хек, как и многие другие исследователи, считал, что атмосфера Земли не увлекает эфир, поэтому в его опыте имеет значение время прохождения лучами света отрезка
AB длиной L в трубке, заполненной водой.Первому лучу потребуется время
t1, равноеt1 = L / (c/n + kv).
Второму лучу потребуется время
t2, равноеt2 = L / (c/n - kv),
где
n – коэффициент преломления воды; k – коэффициент увлечения.Опыты Хека дали отрицательный результат, т.е. никакого эффекта, обусловленного движением Земли относительно звезды, Хек не обнаружил. Это значит, что время
t1 в этом опыте равно времени t2, что соответствует значению k = 0. Другими словами, коэффициент увлечения в этом опыте не соответствует гипотезе Френеля, однако он вполне согласуется с предположением о полном отсутствии “эфирного ветра” в атмосфере Земли - “эфирный ветер”, отсутствующий в атмосфере Земли, не может возникнуть и в трубке с водой, неподвижной относительно той же атмосферы.В 1868 г. Хук поставил другой опыт, “…в котором наблюдал земной источник света в телескоп через двухметровый столб воды. Отсутствие предполагаемого сдвига изображения, обусловленного суточным вращением Земли, Хук объяснил на основе теории Френеля. Он пришел к выводу, что френелевский коэффициент увлечения справедлив с точностью до 2%... В свою очередь Клинкерфус поставил аналогичный опыт с 8-дюймовым столбом воды и получил увеличение постоянной аберрации на 7,1" (по его теории ожидалось увеличение на 8"). Для разрешения этого противоречия серию точных опытов провел в 1871 - 1872 гг. Эйри. Он наблюдал звезду вблизи зенита с помощью вертикально установленного телескопа высотой 35,3 дюйма, заполненного водой. По теории Клинкерфуса за полгода угловое смещение звезды должно было составить около 30", в то время
как на опыте смещение не превышало 1" и лежало в пределах ошибок эксперимента” [3].Постановка этих опытов, как и опытов Физо 1859 г., свидетельствует о непонимании исследователями сути теории Френеля - вследствие полного увлечения эфира атмосферой Земли “эфирный ветер”, обусловленный движением Земли, в атмосфере Земли не возникает, а поэтому не может возникнуть и в телескопе, заполненном водой. Исходя из этого, опыты Эйри являются наиболее достоверными.
Известно, что Майкельсон рассматривал ход лучей в своем опыте с точки зрения внешнего наблюдателя, относительно которого Земля движется с некоторой скоростью
v. Майкельсон считал, что в соответствии с гипотезой Френеля скорость эфирного ветра в атмосфере Земли равна v(1 – 1 / n2). Так как для атмосферы Земли n = 1, скорость эфирного ветра в атмосфере оказывается равной нулю. Другими словами, с точки зрения этого внешнего наблюдателя эфир совершенно не увлекается движением Земли. Поэтому, с точки зрения этого внешнего наблюдателя, скорость света в опыте Майкельсона остается величиной постоянной и равной c, а интерферометр движется относительно неподвижного эфира со скоростью v. В действительности, это не так. Формула Френеля определяет скорость движения эфира внутри движущейся среды относительно наблюдателя, движущегося с этой средой. По отношению к этому наблюдателю скорость движения эфира равна v(1 – 1 / n2). При n = 1 скорость движения эфира оказывается равной нулю по отношению к наблюдателю, находящемуся в атмосфере Земли и движущегося вместе с ней. (Коэффициент преломления воздуха у поверхности Земли равен приблизительно 1,0003. В этом случае скорость эфирного ветра в атмосфере Земли оказывается меньше 18 м/с, тогда как Майкельсон в расчетах принимал v = 30 км/с). Таким образом, предположения Майкельсона о движении эфира внутри атмосферы Земли оказываются правильными с точностью до наоборот. Майкельсон считал, что “По волновой теории, согласно Френелю, эфир, во-первых, должен находиться в покое кроме как внутри (подчеркнуто мной - В.П.) прозрачной среды, а, во-вторых, он должен двигаться в ней (-В.П.) со скоростью, меньшей, чем скорость среды... Вторая гипотеза (Френеля - В.П.)... должна рассматриваться как полностью доказанная... известными экспериментами Физо ... и... нашей собственной работой”. Однако, если гипотеза Френеля может считаться доказанной, тогда, в соответствии с этой гипотезой, скорость эфирного внутри атмосферы Земли относительно интерферометра, неподвижного относительно той же атмосферы, должно быть равно нулю, а не скорости движения Земли относительно эфира, окружающего Землю (точнее, окружающего Землю вместе с её атмосферой). Вместе с тем, как было показано выше, опыт Физо 1851 года подтверждает, по сути дела, факт изменения скорости движения жидкости в поперечном сечении, а вовсе не факт увлечения эфира согласно гипотезе Френеля, которую, кстати, Физо понимал совершенно неправильно.Известно, что в современной теории относительности Френелевская формула сложения скоростей рассматривается как частный случай более общей “релятивистской” формулы сложения скоростей. Если эта формула верна, то, как показано выше, скорость движения эфира в атмосфере Земли должна быть равна нулю. Соответственно, скорость света в атмосфере Земли будет величиной постоянной, независимо от скорости движения Земли относительно чего бы то ни было. В этом случае все другие объяснения нулевого результата опыта Майкельсона-Морли оказываются излишними, а вся теория относительности сводится к одному-единственному утверждению, математическим выражением которого является “релятивистская” формула сложения скоростей: в любой системе координат скорость света есть величина постоянная, независимо от того, находится ли эта система в состоянии покоя или равномерного и прямолинейного движения. И всё!
Итак, опыт Физо не дает достаточных оснований утверждать, что эфир внутри движущихся жидкостей увлекается в соответствии с гипотезой Френеля из-за изменения скорости движения жидкости в поперечном сечении и обусловленного этим искажения интерференционной картины
, наблюдаемой в этом опыте. Возможно, однако, что эти факторы не будут иметь никакого значения при определении степени увлечения эфира твердыми телами.Увлечение эфира твердыми телами. Опыт Харреса
В 1912 г. Харрес выполнил опыт, цель которого заключалась в измерении коэффициента увлечения для стекла. В опыте Харреса лучи света движутся внутри кольца, составленного из прозрачных призм на горизонтальной площадке, которая могла вращаться вокруг вертикальной оси. Ход лучей в установке изображен на рис.3.
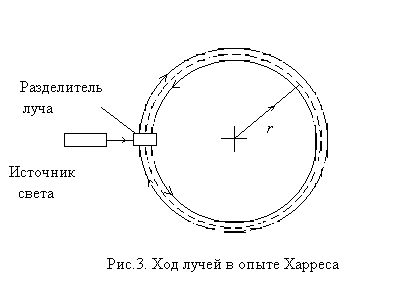
Суть опыта заключается в следующем. Луч света от источника попадает на разделитель, где расщепляется на два луча, один из которых (изображен красным цветом на рис.4) движется в направлении движения установки, другой (изображен синим цветом) – в противоположном направлении. Разделитель, схема которого представлена на рис.4-а, представляет собой призму с двумя зеркальными поверхностями, наклоненными к оси симметрии под углом 45 Когда установка не вращается, т.е. при отсутствии предполагаемого движения разделителя относительно эфира, находящегося внутри кольца, время 
t1 = t2 = L / c / n,
где
L = 2
r – длина окружности кольца; n – коэффициент преломления вещества призм, из которых составлено кольцо в данном опыте.
При полном увлечении эфира внутри движущегося кольца обе зеркальные поверхности разделителя движутся с той же скоростью, что и эфир внутри вращающегося кольца. В этом случае отсутствует движение разделителя относительно эфира внутри движущегося кольца, следовательно, время
t1 движения одного луча равно времени t2 движения другого луча, так как источник света – одна грань разделителя, приемник – другая грань разделителя и среда, в которой движется свет внутри кольца, неподвижны относительно друг друга:t1 = t2 = L / c / n.
При частичном увлечении эфир внутри движущегося кольца движется с некоторой скоростью относительно разделителя, вследствие чего время движения одного луча уже не будет равно времени движения луча. При вращении установки с некоторой угловой скоростью
, время движения лучей будет равно:
t1 = L / (c/n + kv) для одного луча и
t2 = L / (c/n - kv) для второго луча,
где k – коэффициент увлечения эфира внутри движущегося кольца; v = r – линейная скорость вращения кольца.
Тогда разность хода времен
t2 и t1 будет равна:
= t2 - t1 = L / (c/n - kv) - L / (c/n + kv)
= 2Lkv/(c2/n2 – k2v2)
= 2Lkvn2/(c2 - k2v2n2)
= 2Lkvn2/ c2 (1 - k2v2n2/ c2)
Пренебрегая величиной
k2v2/ c2n2 вследствие ее малости, получим: = 2Lkvn2/ c2.
В этом опыте вся установка, включая источник и приемник света, вращалась с одинаковой угловой скоростью. Интерференционная картина фотографировалась на пластинку, которая исследовалась затем в лабораторных условиях.
В опыте Физо интерференционная картина наблюдалась на экране, относительно которого светопроводящая среда – вода в трубке, двигалась с некоторой скоростью
v. Поэтому коэффициент увлечения в опыте Физо должен быть равен k = 1 / n2.В отличие от опыта Физо, приемник света – одна из зеркальных граней призмы вращается с той же скоростью, что и светопроводящая среда – прозрачное кольцо. Поэтому коэффициент увлечения эфира в опыте Харреса должен быть равен
k = 1 – 1/n2. Однако результаты опыта, сообщенные Харресом в его диссертации, не соответствовали формуле Френеля.При полном увлечении эфира все части установки – источник и приемник света - оказывались неподвижными относительно эфира, движущегося вместе с кольцом с той же скоростью. В этом случае разность хода времен должна быть равна нулю, как и в опыте Майкельсона-Морли. В действительности, однако, наблюдалась интерференционная картина, не соответствующая ни полному, ни частичному увлечению эфира.
По результатам опыте Харреса развернулась дискуссия, в которой принимал участие и Эйнштейн, в ходе которой предлагались различные, нередко исключающие друг друга, объяснения результатов рассматриваемого опыта. В конце концов, и этот опыт сочли доказательством Френелевской формулы увлечения эфира, т.е. доказательством “релятивистской” формулы сложения скоростей. В действительности, это не так.
В опыте Харреса лучи света, прежде чем попасть на разделитель, движутся в воздухе (или эфире), не увлекаемом движением кольца. При неподвижном приборе лучи света падают на разделитель, грани которого наклонены под углом 45 градусов к направлению движения лучей света от источника.. При выходе из кольца (после отражения от граней разделителя) лучи движутся к приемнику перпендикулярно плоскости экрана, на котором возникает интерференционная картина. Однако когда прибор вращается, лучи света от источника света к разделителю и обратно движутся иначе.
За время, в течение которого луч света проходит расстояние
l от источника света к разделителю, последний отклонится на некоторый угол, как это изображено на рис. 5. В результате этот луч падает на разделитель под углом, не равным 45 градусам, вследствие чего углы отражения для каждого из разделенных лучей оказываются различными. Соответственно различными оказываются и длины путей для каждого из разделенных лучей, следовательно, и время, в течение которого каждый из лучей проходит свой путь до выхода из кольца.Точно так же, когда луч света выходит из вращающегося кольца, то за время, в течение которого этот луч пройдет расстояние
Таким образом, разность времен
t1 и t2 в опыте Харреса объясняется тем, что часть пути – от источника света к разделителю и обратно - лучи света проходят в воздухе (эфире), не увлекаемом вращением кольца, а часть – внутри кольца в эфире, полностью увлекаемом движением кольца. Однако ни одна из теорий, предложенных для объяснения результатов опыта Харреса, не учитывает этого обстоятельства.Заключение
Анализ опытов Араго, Физо, Харреса позволяет заключить следующее:
1. Коэффициент преломления любой среды, движущейся относительно внешнего источника, зависит от скорости ее движения вследствие изменения частоты света, проникающего в эту среду, согласно эффекту Доплера. Поэтому результаты опыта Араго следует признать недостоверными, а его вывод о независимости коэффициента преломления линзы от движения Земли – ошибочным.
2. Теория Френеля, предполагающая частичное увлечение эфира движущимися средами, основана на недостоверных результатах опытов Араго, и поэтому не может считаться истинной. В СТО формула Френеля рассматривается как частный случай “релятивистской” формулы сложения скоростей. Поскольку формула Френеля не может считаться истинной, не может считаться истинной и “релятивистская” формулы сложения скоростей.
3. Разность хода времен в опыте Физо 1859 г. определена на основании неправильного понимания сути гипотезы Френеля. Вместе с тем, результаты этого опыта вполне однозначно доказывают, что движение эфира, увлекаемого движением жидкостей, сопровождается вполне наблюдаемым изменением интерференционной картины, обусловленным именно движением эфира.
4. Нулевые результаты известных опытов, основанных на измерении скорости света в атмосфере Земли, подтверждают, что скорость света в атмосфере Земли не зависит от скорости ее движения вместе с Землей, что соответствует полному увлечению эфира внутри атмосферы Земли.
5. Точность результатов, полученных в опыте Физо, как и в опыте Харреса, не позволяет однозначно определить соответствие этих результатов гипотезе Френеля. Вместе с тем, анализ опытов Эйхенвальда и Вильсона,позволяет заключить, вопреки общепринятому мнению, что эфир внутри движущихся твердых тел полностью увлекается движением этих тел.
Источники информации: