
На основании уравнения (19) из предыдущего раздела можно утверждать, что эфирная среда обладает некоторой плотностью δ, имеющей электромагнитную природу. В силу очень высокой однородности этой среды (за исключением областей, близких к физическим телам) плотность, как и скорость света С, весьма постоянна. Эта среда является как бы аналогом жидкости, имеющей постоянную плотность и везде присутствующей (распределенной) и которой, в силу этого, можно было бы пренебречь. Вместе с этим, такую среду или вакуум нельзя не считать материальным телом, так как она активно проявляет себя в электрических и магнитных полях и является основой, которая обеспечивает распространение электромагнитных волн (света). Поэтому эфирную среду, рис.8, следует назвать распределенным материальным телом. Физические тела более высокого уровня структуры (электроны, атомы, молекулы и др.) не распределены равномерно в пространстве, как эфирная среда, а геометрически концентрированы и представляют собой сгущения материальной среды в определенных точках пространства. Их следует назвать концентрированными материальными или иначе, физическими телами. Последнее определение имеет еще и тот смысл, что физические тела могут быть обнаруживаемыми физическими приборами. Конечно, характеристики эфирной среды могут быть определены путем возбуждения в ней, например, колебаний. Однако характеристики невозбужденной эфирной среды не могут быть определены, так как любой физический прибор при измерениях будет изменять ее состояние.
Плотность эфирной среды, как и плотность физической, является одним из параметров, определяющим скорость распространения в ней колебаний. Из уравнения (19), приведенного в предыдущем разделе, можно получить, что скорость распространения электромагнитных волн в вакууме равна
 |
(22) |
или
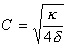 |
(23) |
Из этого уравнения следует, что эквивалентная квадрату скорости распространения света С упругость эфирной среды к должна быть очень велика. Она могла бы быть определена, если была бы известна электромагнитная плотность вакуума δ.
Величину плотности можно найти через волновое сопротивление вакуума. Как известно, волновое сопротивление сплошных сред определяется по формуле:
| R = δC, | (24) |
откуда
| δ = R/C. | (25) |
Значение волнового сопротивления вакуума точно известно [3],
 , , |
(26) |
где μ0 - магнитная проницаемость, ε0 - диэлектрическая постоянная вакуума. Скорость света С также можно выразить через ε0 и μ0:
 , , |
(27) |
Подставляя выражения для R и С в формулу (25), получим, что
| δ = μ0 = 1,25664·10−6, кг·м·сек−2·а−2, | (28) |
где размерность плотности дана в единицах системы СИ.
Итак, магнитная проницаемость μ0 выполняет роль плотности (инерциальной массы) в эфирной среде (вакууме). Теперь воспользуемся формулой (19) А. Зоммерфельда для определения величины скручивающей упругости эфирной среды
| κ = 4/ε0 = 4,51763·1011, кг·м3·сек−4·а−2, | (29) |
Ранее было отмечено (см. раздел 2), что МакКулаг отождествлял диэлектрическую проницаемость ε0 с величиной, обратной упругости [11].
Итак, из определений δ и κ однозначно следует, что эфирная среда (вакуум) имеет электромагнитную природу. Показатели степени при этих величинах дают представление о том, что величина δ очень мала, а упругость эфирной среды κ чрезвычайно высока.
Классическая механика, математическая теория колебаний со всей очевидностью показывают, что волновые процессы могут существовать только лишь при наличии некоторых распределенных масс и упругих сил, соединяющих массы в сплошной континуум. Надо учесть, что для твердых изотропных тел имеется формула, связывающая величины скорости V, массы и модули упругости вещества [52]:
 |
(30) |
где Е - модуль упругости, ρ - плотность вещества.
Сравнение формул (22) и (30) показывает, что они подобны. В формуле (30) модуль упругости Е отражает упругость связей между материальными точками в твердом теле. Плотность вещества ρ отражает массу этих материальных точек.
Из вида формулы (30) следует, что скорость V в твердом (и не только в твердом) теле выше в тех веществах, в которых связи между материальными точками (атомами, молекулами) отличаются большей силой и меньше в тех, в которых атомы и молекулы обладают большей массой. Примерами, подтверждающими это положение, могут служить многие вещества и, в частности, алмаз и свинец. Как известно [55], алмаз отличается большой твердостью и упругостью. Например, величина скорости распространения поперечных колебаний в нем Vs = 12,32 км/c, при плотности ρ = 3,51 г/см3. При этом в свинце скорость Vs = 0,86 км/с, а плотность составляет ρ = 11,6 г/см3. Пропорциональная зависимость между скоростью Vs и величиной 1/ρ - обратной плотности, хорошо выражена для щелочных металлов. Кроме этого, и простые механические модели подтверждают правило - в колебательных системах чем больше масса, тем меньше частота колебаний и наоборот. Соответственно, чем больше упругость, тем больше частота колебаний и наоборот.
Обращаясь к выражению (29) мы видим, что скручивающая упругость эфирной среды κ действительно очень значительна. На это указывает сравнение скорости распространения сдвиговой волны в упругих твердых телах со скоростью света С. Например, скорость распространения сдвиговых волн в самом упругом твердом веществе - алмазе составляет только лишь 4,1·10−5 от величины С. Соответственно, плотность вакуума должна быть очень малой, что и следует из ее величины (28). Естественно, что электромагнитные величины δ и κ невозможно строго сравнивать с соответствующими характеристиками твердых тел в силу их различающейся физической природы.