Тепло. Тепло есть мера кинетической энергии относительно изолированного ансамбля частиц и определяется формулой

где m_i - масса i-той частицы;
      v_i - скорость i-той частицы;
      v_o - скорость всего ансамбля частиц.

Эта мера положительна по определению. Она применима только ко множеству частиц, где корректны статистические оценки (работает закон больших чисел). Применение к ней иных единиц нежели [J], например, калория, чревато путаницей и несовместимостью физических единиц. Некорректным будет использование базовой скорости частиц v_o, отсчитываемой только от части связанного ансамбля. Однако, если мы желаем узнать, как будут взаимодействовать два и более apriori практически изолированных ансамбля, то можно говорить о термодинамике их взаимодействия, выражение для которой, однако, сложнее (1).

Энтропия является информационной мерой сложности, хаоса, свободы поведения этого же множества частиц

S = - S p_j ln p_j [nit] = - S p_j log₂p_j [bit], S p_j = 1,

Традиционно в термодинамике она определяется как интеграл приращения тепла, соотнесенный к определенному уровню температуры T

Исчисление энтропии в других единицах, нежели бит или нит, например, [J/^oK] или [кал/ ^oK] ведет к размерностной путанице и вуалированию ее сущности.

Температура. Понятие температуры является основополагающим в термодинамике благодаря его инвариантности по отношению к конкретным формам материи, позволяющей исследовать энергетику этих форм, сравнивать их термодинамические параметры и получать информацию о свойствах этих форм материи даже если они недоступны прямому наблюдению.

В то время как тепло и энтропия являются распределенными и аддитивными характеристиками материи, температура является точечным локальным параметром, характеризующим интенсивность энергоинформационного обмена в данной точке [5]:

Так как частицы материи могут быть совершенно различной массы, а при их столкновениях выполняются законы сохранения количества движения и энергии, то одинаковой температуре соответствуют совершенно различные скорости частиц. И наоборот, при ограничении степеней свободы одного типа частиц другими (зависимого движения с единой скоростью), их температура будет различной.

Теплоемкость является информационной интегральной мерой структурной сложности вещества. Она определяет суммарное количество степеней свободы внутри вещества, являющихся емкостью для тепла - кинетической энергии частиц

C = dQ / dT [nit], [bit] = dQ/kdT [J / ^oK],

Удельная теплоёмкость определяет количество степеней свободы (информационную емкость) единицы объема [m³, моля, атома, единицы крист. решетки]

Разумным является применение в знаменателе естественных единиц вещества – частиц, атомов, молекул и объемных периодов кристаллической решетки, так как только при этом выявляется связь параметра с количеством степеней свободы.

Теплопроводность есть термодинамическая мера способности вещества проводить тепло

K = (dQ / dT) dx/(dS dt) [nit / ms], [J m/ ^oKm²s]

В термодинамике ХХ века, как правило, рассматривались гомогенные термодинамические системы, на свойствах которых строились обобщения. Однако рассматривая всё вещество как ансамбли “летающих шариков”, абстрагируясь от внутренней структуры вещества, мы оказываемся в плену у ложных обобщений, типа теорем Л. Сциларда и Дж. Неймана.

Реальные частицы материи не являются свободными и неотличимыми друг от друга “шариками”, для которых, например, справедливо выражение для скорости, следующее из (1)

где b – некий постоянный коэффициент.

В результате, шарики разной массы, составляющие идеальный газ, имеют различную скорость, но одинаковую температуру (2).

Стоит только отклониться от “шариковой” модели, мы получим совершенно иной результат, например, путем ограничения степени свободы одного из типов шариков длинными нитями, связывающими их с шарами другого типа. В этом случае средняя скорость обоих типов шаров будет практически одинаковой, а температура – разной.

Когда размеры (масса) частиц отличаются на много десятичных порядков, целесообразно говорить о разных и независимых температурах, так как процесс релаксации таких термодинамических систем практически бесконечен.

Например, частицы эфира не имеют массы, или обладают лишь некоторым инерционным эффектом как присоединенная масса очень небольшого объема, перемещающаяся в идеальной жидкости (самом эфире). В результате, обычное перемещение вещественных частиц (электронов, нуклонов) практически не действует на эфирные частицы. С другой стороны, связанные в эфирные домены (электрон - один из типов эфирных доменов), эфирные частицы имеют ту же скорость что и сам домен. Этим определяется очень низкая температура эфира.

Конкретным примером, относящимся к нашему случаю, является гетерогенная система вещество – электроны – домены эфира - амеры.

Размер амера 1.6 ∙10^-35 [m] в 10²⁰ раз меньше размера стандартного эфирного домена, нуклона, электронной пары. Размер последних в 10⁵ раз меньше размера атома. Если не считать тонких инерционных и гравитационных эффектов, эфир – безмассов, электроны имеют массу в 10⁴ меньше массы атома.

В отличие от атомов и нуклонов, электрон, как выяснено в [7,8] представляет собой эфирный домен, растянутый электрическими силами в тончайшую пленку, плоскость которой всегда разворачивается по нормали к вектору электрического поля, а диаметр определяется его напряженностью в месте расположения электрона. Радиус электрона может варьировать от классического радиуса 2.8 ∙10^-15 [m] почти до радиуса Ридберга – 10^-7 [m]. Поэтому его кинетические свойства резко отличны от свойств шарика и он имеет другое число степеней свободы, меняющееся в зависимости от его положения, связей с атомами и типа кристаллической решетки.

Температура вещества относительно хорошо изучена. Ее измеряют, с ней работают. Не будем на этом останавливаться.

Температура эфира внутри вещества, связанных с веществом доменов эфира, таких как электроны атомных оболочек, меняется быстро, но отлична от его температуры по причине “не-шариковости” термодинамических отношений [проф. Преображенский].

В веществе температура эфира отлична от температуры пустого эфира и, как показано в [5,7], может быть как выше так и ниже температуры пустого эфира. Термодинамические параметры эфира: скорость распространения света, динамическая плотность эфира, его температура однозначно связаны друг с другом, что подтверждает древний закон преломления света

c_s = c_e/n, n = D_s/D_e = D, T_ether=T_oD,

Для понимания этого проиллюстрируем эту общую закономерность на конкретном примере сверхпроводимости.

Приведенная таблица является подтверждением предлагаемой автором термодинамики эфира, модели электрона и парно-электронной проводимости.

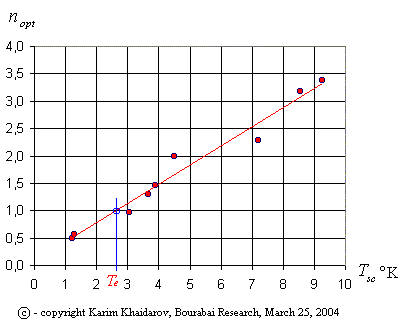
Рис. 1. Зависимость температуры сверхпроводимости от показателя преломления

Однако для ясного понимания этой модели необходимы еще кое-какие уточнения в общефизических понятиях.

Как уже было отмечено выше, вещество есть электроны. Практически все свойства вещества определяются свойствами электрона.

Как показали исследования автора [7,8], в твердых прозрачных веществах электроны совершенно неподвижны и обладают достаточно “изотропным” расположением, чтобы обеспечить прозрачность. Вывод об их практической неподвижности можно распространить и на непрозрачные вещества. Отличие лишь в том, что их валентные электроны обладают незначительной степенью свободы или анизотропии для препятствия прохождению света. Магнитными силами своих токовых петель валентные электроны напрочь привязывают смежные атомы вещества. Именно этим и объясняется механическая прочность и упругость формы твердых веществ. Электроны в них не имеют степеней свободы.

В жидких веществах магнитные силы валентных электронов позволяют атомам совершать ограниченные движения, не разрывающие этих магнитных связей.

В газах межмолекулярные связи электронов нарушены, и молекулы могут свободно “летать”.

Трем фазам вещества соответствует три состояния электронов:

• жесткое связанное, в котором они полностью ограничены,
• состояние гибкой связи, когда они могут совершать движения “нити” или “ткацкой материи”, соскальзывать с одного атома на другой.
• отсутсвия межмолекулярной связи.

Этим трем состояниям соответствуют свои энергии электронов и фазовые переходы.

Химические потенциалы

Классическая физика определяет химический потенциал, как характеристическую энергию любого термодинамического состояния (фазы) вещества, в виде частной производной термодинамического потенциала фазы по числу молей этого состояния

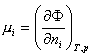
Фактически это характеристическая энергия электронов, определяющая их состояние в веществе.

Таким образом все фазовые переходы в веществе - есть переходы электронов из одного состояния в другое.

Рассмотрим теперь проводимость не с точки зрения артефактной “зонной теории”, а с классических термодинамических позиций.

Согласно предложенной автором прыжковой модели электропроводности [8], ток проводимости в металлах и полупроводниках обеспечивается электронными “куперовскими” парами, существующими малое время, но обладающими большой проникающей способностью и скоростью в веществе.

Переход электронов из валентного состояния в состояние свободной электронной пары и обратно есть фазовый переход первого рода.

Для двухфазной равновесной однокомпонентной системы справедливо классическое уравнение Клапейрона – Клаузиуса [9]

где rμ – теплота фазового перехода (испарения / конденсации) одного моля;
      p – давление фазы;
      R – газовая постоянная;
      T – абсолютная температура.

Уравнение (5) можно переписать в вероятностных терминах для одной свободной частицы, заменяя давление вероятностью данного состояния и считая Φ = const, что естественно для перехода первого рода

Математически это эквивалентно распределению Ферми-Дирака

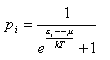
Однако последнее, артефактно трактованное, как наличие нуль-температурных осцилляций у электрона, привело физику в тупик новых парадоксов и абсурдностей.

На самом же деле в данном случае имеется переход кинетической энергии в потенциальную и наоборот по циклу Карно. А потенциальная энергия, как следует из определения температуры (2), не имеет к ней никакого отношения.

Попытаемя исправить это печальное положение, тормозящее неискаженное познание Природы и развитие новых технологий.

Согласно предложенной автором прыжковой парноэлектронной модели электропроводности [8], ток проводимости в металлах и полупроводниках обеспечивается электронными “куперовскими” парами, существующими малое время, но обладающими большой проникающей способностью и скоростью в веществе.

Образуясь в результате слияния двух электронов внешней валентной оболочки атома – донора, то есть атома, имеющего открытую валентную оболочку (металла, полуметалла, полупроводника), электронная пара, приобретя механический импульс, движется через вещество до своего разрушения. В месте разрушения она снова разделяется на два электрона, которые захватываются внешними оболочками близлежащих атомов.

Взаимодействие магнитных полей электронов - движения элементарного (амерного) заряда по периметру эфирного домена – электрона, есть та сила, которая сцепляет электроны в пару, уменьшая его размеры до величины менее 10^-14 [m].

Взаимодействие электрических полей и температура окружающего вещества – это то, что разрушает сцепленную пару электронов.

Большой поток этих пар, обладающих высокой проникающей способностью, создает поток тепла и ток проводимости, в статистике подчиняющийся закону Ома

j = E/σ [A/m²],

Детерминированная часть вектора импульса электронной пары в момент ее образования определяется асимметрией кристаллической решетки и вектором электрического поля, а случайная - тепловыми флуктуациями.

Другими словами имеется два компонента импульса электронной пары. Один из них определяется электростатическим полем приложенным к месту их рождения. Другой, стохастический компонент вызван произвольным начальным толчком "броуновского" движения атомов.

Для избежания перегрузки статьи, интересующихся подробностями этой модели отсылаем к [8], а ниже рассмотрим конкретные случаи применения этой теории.

Укажем лишь, что мы будем использовать свойство электрона изменять свои размеры (радиус этой тонкой пленки) в зависимости от напряженности электростатического поля

где ε – диэлектрическая проницаемость эфира [F/m];
      τ – линейная плотность заряда [C/m];
      E – напряженность электростатического поля [V/m].

Можно ли объяснить наблюдаемые физические явления с помощью предлагаемой эфирной теории, не прибегая к артефактной зонной теории и не обращаясь к несуществующим электронам проводимости? Попробуем.

Для выявления конкретных свойств предлагаемой модели рассмотрим процесс преодоления электронными парами полупроводникового перехода. Как известно, p-n, p-i переходы представляют собой узкую пограничную область – “запирающий слой”, заряженную подобно электрическому конденсатору. На одной стороне находится зона с избытком валентных электронов, дополняющим атомы до полной электронной оболочки, а с другой, наоборот, отнятыми излишними электронами. Этот тонкий переходной слой становится похожим на валентный диэлектрик, как например, Na⁺Cl ^– , непроводящий электрический ток.

Другими словами, в этом случае состояние атома с четным количеством электронов в валентной оболочке более стабильно (имеет меньшую потенциальную энергию), чем сбалансированое по заряду состояние атома (не заряженный атом), но с нечетным количеством электронов во внешней оболочке.

“Лишние” электроны перехода являются барьером для проводимости. Плотность (электрическое сопротивление) этого барьера зависит от общей площади составляющих его электронов, приходящихся на единицу поверхности барьера

где R – радиус электрона из (7);
      N – количество электронов, приходящихся на единицу поверхности барьера.

Другими словами, фиксированные электроны скопившиеся в пределах n-стороны перехода и отсутствие электронов с p-стороны перехода создают электростатический барьер пропорциональный S.

Радиусы электронов уменьшаются с увеличением напряженности электрического поля, действующего на переход. N является функцией приложенного к переходу напряжения, таким образом, что N уменьшается для прямого тока и увеличивается для обратного. В результате мы получаем близкую к квадратичной вольт-амперную характеристику прямого перехода

I = U/R_np = U²/ s₁ [A],

вплоть до исчезновения барьера, после чего сопротивление цепи определяется полупроводниковой базой, и близкую к корневой – для обратного тока

I = U/R_np = √U/ s₂ [A],

Эти зависимости много ближе к реальным, нежели полученные из зонной теории.

Наличие выпрямляющих свойств переходов не зависит от знака разницы работ выхода материалов, как следовало бы из зонной теории, а определяется только наличием барьера ионизирующих атомы электронов.

Толщина запирающего слоя увеличивается при увеличении обратного напряжения не из-за искривления несуществующей “зоны”, но увеличения слоев атомов, вовлеченных действием электрического поля в ионизацию, достраивающую внешнюю оболочку атома до заполнения или, наоборот, отнимающую электроны до опустошения недостроенной валентной оболочки атома.

Как видно, данная модель не нуждается в наличии “зонной проводимости”, но только в наличии “ионного” запирающего слоя.

При превышении напряженности электрического поля запертого p-n перехода величины порога срыва электронной пары с наружной “ионизированной” оболочки атомов переходного запирающего слоя происходит полевой пробой. Его нельзя называть “туннельным”, так как никакого туннеля нет. Это лишь воображение в рамках артефактной зонной теории.

Именно в соответствии с этим на вольт-амперной характеристике обратного перехода имеется резкий излом. Именно поэтому могут работать стабилитроны – диоды Зенера, напряжение полевого пробоя которых определяется прочностью связи валентных электронов ионов запирающего слоя.

Напряжение стабилизации таких диодов определяется только прочностью сцепления “ионизирующих” электронов перехода с атомами и шириной запирающего слоя.

С существующей зонной теорией не согласуются результаты экспериментов, которые свидетельствуют о том, что любые переходы Ме - полупроводник являются выпрямительными, независимо от относительных значений работ выхода. Однако в рамках предлагаемой модели их легко объяснить тем, что выпрямляющие свойства перехода зависят вовсе не от характеристик “зон”, а от наличия “ионизированного” запирающего слоя, который возникает всегда при переходе от одного типа проводимости к другому. Более того, он возникает даже на переходе одного типа проводимости, если имеются условия для отнятия электронов у одного материала другим, то есть дополняющей валентную оболочку “ионизации”.

При более высоких напряженностях, нежели уровень возникновения полевого пробоя имеет место лавинный пробой, связанный с тем, что электронные пары при разгоне в электростатическом поле выбивают новые пары из атомных оболочек.

Объяснение его не столь отличалось бы от существующей электронной теории, если бы не одна существенная особенность парноэлектронной проводимости – чрезвычайно малый размер электронной пары.

С этим связана возможность формирования за счет силы Ампера чрезвычайно тонких и, следовательно, обладающих большой удельной мощностью токовых шнуров. Возникающие токовые шнуры приводят к другим интересным и необъяснимым с точки зрения Ферми-Дирак-Шрёдингеровской физики явлениям.

Теперь перейдём к явлениям, которые вовсе не может объяснить пусто-релятивистская и логически искривленная физика

В рамках предлагаемой модели было бы естественным ожидать того, что высокая напряженность поля в проводнике или полупроводнике должна срывать электроны с наружных оболочек атомов.

Действительно, при напряженности 10⁶ [V/m] в кремнии и 10⁵ [V/m] в германии такое наблюдается в виде “отклонения от закона Ома” [9], то есть резкого увеличения удельной проводимости. В металлах, где энергия связи электронов значительно меньше, это явление должно наблюдаться при напряженностях 10³ – 10⁴ [V/m].

Наблюдение его осложнено тем, что еще до таких уровней напряженности электрического поля проводник разрушается под действием джоулева тепла, выделяемого током. Можно ли наблюдать это явление реально? Да. Это возможно и давно наблюдаемо по крайней мере в трёх случаях:

• по металлу течет большой импульсный ток с большой скважностью импульсов и временем импульса менее времени жизни электронной пары;
• по металлу течет большой высокочастотный ток, порождающий скин-эффект;
• большой ток течет через зернистый резистор с малыми контактными площадками между зернами.

Реально эти три случая встречаются вместе, усиливая эффект друг друга.
Остановимся на конкретных примерах.

Трансформатор Тесла [10-11]. Более 100 лет назад гениальный экспериментатор Никола Тесла создал высоковольтную линию передачи электрической энергии, по к торой передавал, вопреки омическим расчетам много большую энергию. Источником этой линии передачи был повышающий трансформатор с “оборванным” одним проводом.

Схема такого рода дает в нагрузку короткие импульсы тока, время которых меньше времени жизни электронных пар. Кроме того, так как спектр частот линии довольно высок, основной ток сосредоточен в тонком поверхностном слое проводника, что обеспечивает увеличение плотности тока – напряженности поля с одной стороны, отвод джоулева тепла от проводящей поверхности – с другой.

Другими словами, сравнительно низкая температура металла создает условие низкого электрического сопротивления в пределах поверхностного слоя металла, где может существовать большая плотность тока.

Катушка индуктивности Голубева [12]. Виктор Голубев проводил эксперименты с высокочастотными катушками индуктивности большой добротности. Он обнаружил уменьшение омического сопротивление проводника катушки при протекании больших резонанснвых токов.

Вилка Авраменко [13]. Станислав Авраменко соорудил вариант трансформатора Тесла, прибавив к нему диодный выпрямитель. Последнее позволяет получить большие импульсные токи при сравнительно низком напряжении трансформатора.
Так как схема некритична к омическому сопротивлению линии, то наблюдается “нарушение закона Ома”.

Другими словами, когда мы создаем очень короткие импульсы тока, то сопротивление короткой электрической линии не имеет значения, поскольку время жизни электронной пары, рожденной источником, достаточно для преодоления расстояния линии без разрушения.

При высоких напряженностях электрического поля на границе металл – вакуум возникает взрывная эмиссия электронов, характеризующаяся сверхбольшой 10¹² - 10¹³ [A/m²] плотностью тока в малой области.

Необъяснимая с точки зрения “зонной теории” такая плотность тока может возникнуть при взаимодействии электронных пар малого размера. Сила Ампера формирует из электронных пар тончайшие токовые шнуры. Плотность тока в них такова, что это приводит к разрушению электронных оболочек атомов в малом объеме вещества. Температура этого объема поднимается практически мгновенно до значений в миллионы градусов. Происходит вскипаение и микровзрыв металла [14-22].

В этом случае ядро атома становится “голым”, и возможны ядерные реакции как слияния ядер, так и их распада под действием потока электронных пар сечением взаимодействия эквивалентным размеру нуклона. Кроме того был бы естественным электронный захват или даже двойной электронный захват.

Сотрудниками РНЦ "Курчатовский институт" Уруцкоевым Л. И., Ликсоновым В. И. и Циноевым В. Г. [23] был проведен эксперимент по исследованию продуктов электроразрядного взрыва титановой проволоки в герметичном полиэтиленовом баллоне, наполненном водой.

В результате этого эксперимента было выявлено возникновение в результате взрыва новых химических элементов, ранее не присутствовавших в установке.

Среди этих элементов оказались Na, Ca, Fe, Ni, Au, Pb.

Предлагаемая эфирная модель электропроводности позволила по-другому и адекватно объяснить проводимость в металлах и явление сверхпроводимости.

Найденная простая связь между критической температурой сверхпроводимости, удельной теплоемкостью и информационными мерами структурной организации вещества (как описанный коэффициент трансформации динамической плотности эфира D), оптической плотностью и скоростью света в веществе открывают научную альтернативу слепому поиску новых сверхпроводящих веществ.

Предлагаемая теория проясняет истинную природу вещества как формы существования эфирных электронов.

Благодарность

Автор благодарен физику Линдону Ашмо (Lyndon Ashmore) за его замечания и редакцию английского варианта статьи.

Карим Хайдаров
Боровое, 25 марта 2004 г.
Дата зарегистрированного приоритета: 26 марта 2004 г.