![]()
(1)
© Copyright - Karim A. Khaidarov, March 25, 2004.
"I shall rescue him; I shall protect him, for he acknowledges My name"
[Ps. 90/91]
In this paper, the presence of the ether in the Universe will be taken as a fact [1], and considered as a united quasi-isotropic, practically incondensable and perfect elastic medium that is the main basic matter, the carrier of the whole energy and all processes that occur in the Universe. This is based upon the working model [2-6], that presents the ether in the manner of a two component medium - corpuscular and phase and it is upon this model that we will consider the ethereal theory of conduction. We will show that both the theory of electronic conduction of Drude-Lorentz and the zonal theory of conduction are relics of the past. Within the framework of the theory of ether [1-6], developed by the present author and the model of ethereal electron offered earlier, this paper presents a new theory of conduction based on pair-electronic motion.
The Source of the Artifacts
Credo quia absurdum.
St. Augustine
The theoretical physicists, who are necessary to describe the mathematics in physics, are prone to use "curvature" to describe physical phenomena, whether it is the curvature of space, volume, velocity, time or the curvature of energy levels. It would appear that theorists resort to the ungrounded notion of curvature whenever their speculative theorizing does not fit with the real facts.
The theory of conduction of Drude-Lorentz has existed for over 100 years, and postulates the presence of an electronic gas in metals. Peacefully coexisting with this, is a monstrous 104 K temperature of the electrons and, following on from the postulates of this theory, this temperature results in a predicted pressure. At the same time that this theory has been in existence, and since the Rutherford epoch, it has been known that the atom is practically empty. That is to say the whole of its volume, excluding the nucleus (which is 10-15 part of its volume), is occupied by electrons, and that these electrons are a "glue" that binds the atoms into molecules, and the molecules into solid and liquid bodies.
Bohr's theory describing the atom as a planetary system is purely speculative but it has not resulted in any criticism. It is now nearly a century since Bohr first put forward the atomic model and we have yet to have the following questions answered:
From then on, things did not improve as this practice of ‘logical nonsense’ was continued. Properties that only applied to a statistical ensemble were applied illegitimately to a single electron and the experiment on the diffraction of a single electron was counted as a victory for this approach - with the consequence that the illogical and incorrect statistics of a single electron remained. Instead of acknowledging the fact that the medium acts upon the path of an electron (in a similar way as air or water acts on light) or accepting that the shock wave, which spreads from particle to particle and reflects from obstacles thereby influencing their path, there appeared the next "logical twist" in the story - that the electron is both a wave and a particle at the same time. The laws of macrocosm do not act within microcosm.
The aether theory, consisting of particles moving within an original medium was already well developed but these artifact ‘pseudo-theories’, supported by complex mathematics that hid their absurdity, remained.
The Notions of Aethereal Electron and Electronic Pair
In paper [7] it was shown that electrons are strictly at rest, at least in transparent materials. The effects of this is an absence of Bohr's orbits within the atoms and so we must search another explanation for the electronic shells in atoms.
In the same paper the ethereal model of the atom was offered. It doesn't require the movement of electrons nor the logically inconsistent notion of an electron as wave and particle simultaneously. Using this model has allowed us to forecast the density and optical characteristics of transparent materials to a fine precision.
In works [3, 8] it was shown that it is possible to present the electron in the form of electrified ether domains with a captured electromagnetic wave in a mode of full internal reflection. Herein, the proposed model explains the change of the electron capture cross section, as a change in the size of the electrostatic field strength, and spin, as a rotation of the elementary electric charge on surface of this ethereal domain.
It was also shown that the phenomenon of electrical conduction in metals and semiconductors is described, not by the movement of solitary electrons, but by the movement of ethereal electronic pairs. These pairs are different from the notion of "Cooperian pairs" in their size. Ethereal pairs have a size of the order of 3·10-15 [m], and not 10-10 [m] or more, as in "wave theory" of the electron. Due to this feature of electronic pairs, the substance is permeable for ethereal pairs, and the phenomenon of superconductivity and super fluidity exist.
It is now possible to say that the zonal theory is an artifact because free electrons do not exist, and, as a consequence, neither does the "conduction band" in metals.
The Atoms of metals, by their nature, are donors of electronic pairs. Being efficient carriers of electrical charge, pulse and, consequently heat, electronic pairs, even in the measly concentration 105 - 1012 [cm-3] will result in a high electrical conductivity and specific heats for metals. In a low concentration, they have a negligible contribution to the specific heat of metals, which changes sharply when turning to super conductivity because of the rapid increase in the number of electronic pairs.
At room temperature, the life time of an electronic pairs is very short, and has values of the order 10-4 - 10-8 [s] depending upon the material. Two adjacent electrons in the valence band collapse to form a very small pair, 1/30000 of their original size. As a result of this collapse, potential energy of the original electrons is transferred to the kinetic energy of the created pair. The newly created electron pair fly off at great speed from the parent atom and are highly penetrating due to their speed and small size. Eventually, the electronic pair decays and its electrons are captured by nearby atoms which gain the energy and charge of the electron pair.
The destruction of an electronic pair derives from a thermodynamic interaction with the electrons in an atom. So the original temperature Te of the electron pair defines the pair ‘life time’. From a preliminary evaluation by the author, a threshold of stability for the electronic pair, that is to say the critical temperature of substance Tsc, below which the life time of the electronic pairs sharply increases, is:
T
sc = 1.148 ·TeThe phenomenon of superconductivity appears if the temperature of the material falls below this temperature, that is, below the temperature at which electronic pairs do not decay.
So, at each temperature, a conductivity (according to our model), is supported by electronic "Cooperian" pairs.
As we have already realized, Cooperian pair carry a fixed amount of heat (thermal energy) and have a practically fixed pulse at creation. If the thermal conductivity of metals basically depends upon the motion of these pairs, then, naturally, we must consider that the amount of heat carried is proportional to amount of pairs created and their average life time. If the critical temperature at which superconductivity and super fluidity occur depends some way on the composition and structures of the material, then the structure of the atoms and the structure of the crystal lattice must define these values. Let us try to understand this.
For this, it is necessary to define the notions of heat, heat capacity and heat conduction, which are in a mess both dimensionally and in terminology, due to historical reasons.
Notions of Heat, Temperature, Heat Capacity and Heat Conductivity
There are three kinds of lies: lies, damned lies and statistics
Benjamin Disraeli
Heat.
Heat is a measure of the kinetic energy of a comparatively insulated ensemble of particles and is defined by following formula|
|
(1) |
where mi - is a mass of i-th particle;
vi - is a velocity of i-th particle;
vo - is the velocity of hole ensemble.
The value of Q is always positive and it should be noted that the expression is only applicable to an ensemble of particles - where correct statistical estimates can be made (i.e. where the Law of Large Numbers applies). Using units other than Joules [J], (for instance, calories), is fraught with difficulties by the mess and inconsistency of physical units. Using the base velocity of particles vo, determined from only part of the bounded ensemble will be incorrect. However if we want to know, how two and more ‘a priori’ practically insulated ensembles will interact, it is possible to talk about the thermodynamics of their interaction, but the expression obtained will be more complex than (1).
Entropy is a measure of the chaos, behaviour, and the degrees of freedom of particles in the ensemble
S = -
S pj ln pj [nit] = - S pj log2pj [bit], S pj = 1,where pj is probability of j-th state of particles in the system.
Traditionally in thermodynamics it is defined as an integral of increments of heat, correlated to a determined level of temperature T
![]()
Calculation of entropy in other units, except the bit or nit, for instance, [J/oK] or [Cal/ oK] leads to a dimensional mess and hides its true essence.
Temperature. The Notion of temperature is background in thermodynamics due to its invariance to concrete forms of matter, allowing the study of energy of these forms, compare its thermodynamic parameters and get information on characteristics of these forms of matter even though they are inaccessible for direct observation.
Whilst heat and entropy are distributive and additive (extensive) properties of matter, temperature is an intensive local parameter, characterizing intensity of energy-informational exchange in observed point [5]:
|
T = dQ / dS [J/nit] = dQ / kdS [oK], |
(2) |
where dQ - is an increment of heat energy [J];
dS – is an increment of entropy [nit].
k - is the Boltzmann constant, a factor required to change the unit of temperature from [J/nit] into Kelvin, 10 K = 1.38 ∙10-23 [J/nit] = 2.0∙10-23 [J/bit].
Particles within matter can have a wide range of different masses but, in collisions the laws of conservation of momentum and energy apply, so that for the same temperature the particles will have a correspondingly wide range of different velocities. Conversely, the number of degrees of freedom of one type of particle is restricted by others (where the particles move as a group with a united velocity), and so their temperature will be different.
According to the second law of thermodynamics in systems where there is no "Maxwell's demon", that is to say a nonlinear sorting of particles upon their energy, heat always goes from a hot body to cold one. Thereby, the signs dQ and dS are always the same and this stands to remind everyone who tries to talk about a ‘negative temperature’.
Heat Capacity is an informational integral measure of structured difficulty of substance. It defines total numbers of freedom degree materials inside, being capacity for heat - kinetic energy of particles.
C = dQ / dT
[nit], [bit] = dQ/k dT [J / oK],where dQ – is an increment of heat energy [J];
dT – is an increment of temperature [J/nit], [oK].
k – is the Boltzmann constant, a factor required to change the unit of temperature from [J/nit] into Kelvin, 10K = 1.38 ∙10-23 [J/nit] = 2.0∙10-23 [J/bit].
Specific Heat quantifies degrees of freedom (information capacity) of volume unit [m3, mole, atom, crystal lattice unit]
|
c = dC / dV [nit/m3], [J / oKm3] |
(3) |
where dC – is an increment of heat capacity [nit];
dV – is an increment of volume [m3].
In the denominator it is reasonable to use ‘natural units’ of the material - particles, atoms, molecules and three-dimensional periods of the crystal lattice, since only in these cases can the relationship between the parameter and numbers of freedom degree be revealed.
Thermal conductivity is a thermodynamic measure of the ability of a material to conduct heat
K
= (dQ / dT) dx/(dS dt) [nit / ms], [J m/ oKm2s]where dx/dt – is the velocity at which heat flows [m/s];
dS – cross sectional area across which the heat flows [m2].
After an analysis of the thermodynamic terms, it becomes clear that the empiricalyl found formulas, in which off-balancing degrees k and T, are invalid or untrue interpretted (it is impossible to use the factor of recalculation in other times, than recalculated parameter).
Temperature of a Complex Ensemble of Particles
In 20-th century thermodynamics, as a rule, homogeneous thermodynamic systems are considered on characteristics which were built upon generalizations. These generalizations considered all materials as an ensemble of "flying balls", independent of the internal structure of the material. We find ourselves trapped in the captivity of these false generalizations, as for instance L. Szilard's and J. Neumann's theorems.
Following the theoretical idealization given in equation, (1), we can find the expression for the velocity of particles of different mass:
|
vi2 = bkT / mi , |
(4) |
here b – is some constant factor,
As a result, balls of different mass which form an perfect gas have a different velocity, but the same temperature (2).
As we sway from the "ball" model, we will get a completely different result. For instance, the number of degrees of freedom of one of types of ‘ball’ is restricted by threads, linking them with balls of another type. In this case the average velocity of both types of balls will be practically the same, but their temperature will be different.
When the mass of particles differ significantly, it is reasonable to talk about different and independent temperatures, since the process of relaxation of such thermodynamic systems is practically endless. For example, ether particles have no mass, or at least, they have very few inertial effects being as they are a joint mass of very small volume moving in an perfect liquid (the ether itself). Additionally, the usual movement of substantial particles (electrons, nucleons) has no effect in practice since they can't act on the ether particles. On the other hand, binding in domains (electron is one example of it), means that the ether particles have the same speed as the domain itself. This defines the ether's very low temperature.
Temperature of the Substance, Electrons and Ether
The physical example, referring to our case, is a heterogeneous system: atoms - electrons - ether domains - amers.
The amer has a size of 1.6x10-35 [m], being 1020 times less than the size of the standard ethereal domain, nucleon. The size of the electronic pair is 105 times less than an atom. Excluding any fine inertial and gravitational effects, the ether is mass less. Electrons have a mass 104 times less than that of the atom.
Unlike atoms and nucleons, the electron, as it is described in [7, 8] presents itself as an ethereal domain, strained by the electric force into a very fine film, the plane of which always turns around a normal to the vector of the electric field, but the diameter of which is defined by the electric field strength of this field in the place where the electron is located. The radius of the electron can vary from the classical radius 2.8x10-15 [m], up to the Rydberg radius of 10-7 [m]. So its kinetic characteristics are sharply different from the characteristics of those of a ‘ball’ and it has differing numbers of degrees of freedom, which change according to its position, relationships with other atoms and the type of crystal lattice.
The temperature of the material itself has been comparatively well studied and measured and so we can take this for granted and move on.
The temperature of the ether within the substance, such ether domains, electrons binding with substance (i. e. electrons in atomic shells), changes rapidly, but differs from the substance temperature by reason of the "non-ball" thermodynamic relationships.
In a substance, the temperature of the ether differs from the temperature of the empty ether and, as it is shown in [5,7], can be both higher or lower than the temperature of the empty ether. The ether thermodynamic parameters: velocity of light propagation, ether dynamic density and its temperature are uniquely bound with each other and confirm the ancient law of refraction of light
c
s = ce/n, n = Ds/De = D, Tether=ToD,where cs – is the velocity of light within the substance;
ce - is the velocity of light in the empty ether;
n - is substance refraction factor compared to the ether;
Ds – is ether dynamic density in substance;
De - is dynamic density of empty ether;
Tether – is the temperature of the ether in the substance;
D – is a transformation factor of the dynamic density.
As an illustration, let us examine a physical example of super conductivity.
In transparent materials the temperature of the ether is practically uniquely defined by the optical density – the factor of refraction. For metals and other opaque materials, materials with a strong anisotropy, the situation is more complex, because it is necessary to take into account the dispersion and geometry of light path. However, for those materials the situation is practically unambiguous. This is shown in table 1, where the parameters of superconductivity and optical density of simple materials are shown. Since these materials have a simple construction, the ratio D of ether temperature, defined by the structure of the material (the crystal lattice, the number of degrees of freedom), presents an uncomplicated fraction. The idea of the factor D is similar to the notion of specific heat (3), considered above, being by nature a measure of information in terms of Shannon information theory.
Table 1. Dependency Tsc of superconductivity on ether temperature Te
|
Substance |
T supercond |
T ether |
λ [nm] |
n optic |
D +0.148 |
D |
|
Al |
1.224 |
1.220 |
500 |
0.5 |
0.448 |
0.3 |
|
Ba II |
1.3 |
1.310 |
177 |
0.57 |
0.481 |
1/3 |
|
Ba III |
3.05 |
3.126 |
113 |
0.97 |
1.148 |
1.0 |
|
Bi II |
3.9 |
3.807 |
450 |
1.46 |
1.398 |
1.25 |
|
Bi III |
7.25 |
7.210 |
- |
- |
2.648 |
2.5 |
|
Bi VI |
8.55 |
8.572 |
850 |
3.18 |
3.148 |
3.0 |
|
CaSi2 |
14.0 |
14.020 |
- |
- |
5.148 |
5.0 |
|
CsBi2 |
1.5 |
1.492 |
- |
- |
0.548 |
0.4 |
|
Hf5Re24 |
5.86 |
5.849 |
- |
- |
2.148 |
2.0 |
|
Nb |
9.25 |
9.185 |
2800 |
3.37 |
3.373 |
3.25 |
|
Nb3Al-Ge |
19.4 |
19.464 |
- |
- |
7.148 |
7 |
|
Nb3Sn3 |
18.088 |
18.102 |
- |
- |
6.648 |
6.5 |
|
NbN |
17.8 |
17.830 |
- |
- |
6.548 |
6.4 |
|
Sb |
3.672 |
3.671 |
400 |
1.3 |
1.348 |
1.2 |
|
Ta |
4.488 |
4.488 |
300 |
2.0 |
1.648 |
1.5 |
|
Pb |
7.208 |
7.210 |
2000 |
2.28 |
2.648 |
2.5 |
|
V3Ga |
16.8 |
16.741 |
- |
- |
6.148 |
6.0 |
|
ZrW2 |
2.2 |
2.218 |
- |
- |
0.815 |
2/3 |
Table 1 confirms the ether thermodynamics model of electron and pair-electronic conductivity, as proposed by the author.
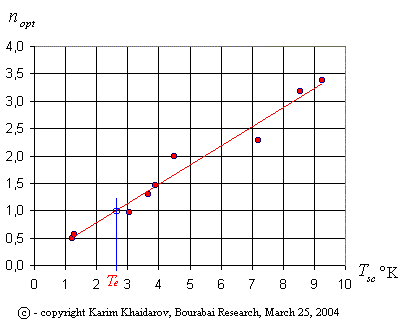
Fig. 1. Dependency of temperature of superconductivity on factor of refraction
However, for a decisive understanding of this model it is necessary for us to revise some of the general physical notions.
Substance, Phase States and Transitions
Electron is infinite.
V. I. Lenin, FCT V.18
As already noted above, the substance is the electrons. Practically all the characteristics of the substance are defined by the electron properties.
It was shown by the present author [7, 8], that in solid, transparent materials, the electrons are absolutely still but have sufficient "isotropic" location to provide the transparency. It is possible to extend this conclusion, of the stillness of the electron, to include opaque materials. The difference consists only in that here, the valence electrons have a small degree of freedom, or have anisotropy, to block the passage of light. By the magnetic forces of its own current loops, valence electrons completely fasten the adjacent atoms of the material together. This explains exactly the mechanical toughness and ‘bounce’ of the solid state. The electrons within them do not have any degrees of freedom.
In fluid materials, the magnetic force of valence electrons allow the atoms to make a limited motion, without breaking these magnetic relationships.
In gases the intermolecular relationships of electrons no longer exist, and molecules can "fly" liberally.
There are three states of the electron, corresponding to the three phases of the substance:
There are three levels of electron energy, corresponding to its states and phase transitions.
Chemical Potentials
Classical physics defines chemical potential, as being indicative of the energy of any thermodynamic state (phase) of the substance, as a partial derivative of the phase thermodynamic potential with respect to the numbers of moles in this state:
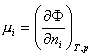
Practically, this is indicative of the energy of the electrons, defined by its state in the substance.
Thereby all phase transitions in a substance are caused by the electrons in the material changing from one state into another.
Now let us consider the process of conduction, not from standpoint of the old and outdated "zonal theory", but from the classical thermodynamic position
.Classical Thermodynamics in the Model of Conduction
True knowledge is a knowledge by causes.
Francis Bacon
According to the jumping model of conduction [8], put forward by the author, conduction current in metals and semiconductors is provided by electronic "Cooperian" pairs, existing for a short time, but having a large penetrating ability and velocity within the substance.
The electron, changing from the valence condition into the condition of a ‘free electronic pair’ and back is the first-kind of phase transition.
The classical Clapeyron-Clausius equation for a two-phase single component system in equilibrium [9] is valid
|
|
(5) |
where r
μ – is the energy transferred in the phase transition (evaporation, condensation) for one mole;It is possible to express equation (5) into probability terms for one free particle, changing pressure to the probability of it being in its present state and considering that thermodynamic potential
Φ during first-kind transition is constant. Then, we may rewrite (5) as|
|
(6) |
Mathematically equ. (6) is equivalent to the Fermi-Dirac distribution
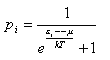
However the latter is historically interpreted as a presence of a zero-temperature oscillation of the electron and has brought physics to a dead-end, consisting of new paradoxes and absurdities.
In truth, in the Carnot cycle, kinetic energy is changing into potential energy back again. But potential energy does not follow on from a determination of the temperature (2), and has no relation to the temperature value at all.
Let us try to correct this sad situation, by supporting a non-distorted view of Nature and developing new technologies.
Aethereal Pair-Elecronic Model of Conduction
According to the pair-electronic jumping model of conduction [8], put forward by the author, conduction currents in metals and semiconductors are provided by electronic "Cooperian" pairs, existing for a short small time, but having large penetrating ability and velocity within the material.
Originating as a result of the merging of two electrons from the external valence shell of an atom - donor, that is to say, an atom having an open valence shell (the metal, semi-metal, semiconductor), the electronic pair gain a mechanical pulse and move through the material up to their destruction. In the place of their destruction it divides into two electrons once again. The electrons are captured by the external shells of nearby atoms.
The interaction of the magnetic fields of the electrons with the motion of elementary (amereal) electrical charge along the perimeter of an ethereal domain – electron provides a force, which couples the electrons into pairs, reducing their overall size to less than 10-14 [m].
The interaction of the electric fields and the temperature of the surrounding materials destroy a coupled pair of electrons.
A large flow of these pairs, having high penetrating ability, creates a flow of heat and conduction current, which statistically complies with Ohm's Law.
j = E/
σ [A/m2],where j – is electric current density;
The deterministic part of the vector for the electronic pair pulse at the moment of its origin is defined by asymmetry of the crystal lattice and the vector of the electric field, but the random part is defined by heat fluctuations. In other words there are two components of the electronic pair pulse. One of them is determined by the electrostatic field applied at the place of origin. The other is the stochastic component caused by the random initial push of Brownian motion.
In the interests of brevity, anyone interested in the details of this model should consult [8], but below we will apply the theory to a practical example.
Here we will use the phenomenon of the change in size of an electron (radius of this fine film) dependent upon the electric field strength of the electrostatic field.
|
R = τ / 2πεE [m], |
(7) |
where
ε – is dielectric permeability of the ether [F/m];Is it possible to explain the observed physical phenomena by means of the proposed ethereal theory, not referring to the dated zonal theory and without resorting to the
nonexistent electrons previously thought responsible for conduction? Let us try.Direct and Inverse Current Through a p-n Junction
To demonstrate the concrete features of this proposed model we will consider the process of a semiconductor junction, overcome by an electronic pair. As is well known, a p-n, p-i junction presents itself as a narrow border area – a "locking layer" charged like an electrical capacitor. On one side of it, the layer has an abundance of valence electrons, complementary doping atoms completing the electronic shells, but on the other side we have the contrary, a layer without valence electrons caused by doping atoms of another kind and providing a different type of conductivity. This fine transitional layer acts like a valence dielectric such as, Na+Cl - , non-conducting to electric currents. In other words, in this case the state of the atomic valence shell with an even number of electrons is more stable (lower energy potential) than that of a charge balanced atomic state (not a charged atom) having an odd number of electrons in the external shell.
“Spare" electrons at the junction are a barrier to conductivity. The density of this barrier (and hence the electrical resistance) depends upon the cross sectional area of the electrons that form it and the number of electrons per unit square of surface of barrier.
S
= πR2N,where R – is radius of electron from (7);
N – is number of electrons per unit square of surface of barrier.
In other words, fixed electrons agglomerated within n-side of junction and electron absence on the p-side of junction create electrostatic barrier proportional to S.
The radii of electrons decrease with increasing of electric field intensity, acting on junction. N is a function attached to turning the voltage, thereby that N decreases for direct current and increases for inverse. As a result we get close to square-law volt-ampere characteristic of direct current
The radius of the electrons decreases with an increase in the strength of the electric field, acting at the junction. N is a function attached to turning the voltage, thereby that N decreases for direct current and increases for inverse. As a result we get close to the square root-law volt-ampere characteristic of inverse current
I = U/Rnp = √U/ s
2 [A],and close to the square-law (parabolic) - for direct current
I = U/Rnp = U
2/ s1 [A],The latter applies up to disappearance of the barrier, after which the resistance of the chain is defined by semiconductor base, because the resistance of the base becomes greater than junction.
Here s1, s2 are constants whose values depend upon the direction of the current and the material of junction [V Ohm].
These dependencies are much closer to the real situation, than those obtained by zonal theory.
The presence of the rectifying characteristics of the junction does not depend upon the sign of different materials, the work done on escaping (electronic work function), as it would be following on the zonal theory, but is defined only by the presence of a barrier, consisting of ionized atoms. In other words, the height of barrier depends only on accumulating extra electrons or electron holes, but not from the type of junction.
The thickness of the locking layer increases when the inverse voltage increases, not because of the effects of nonexistent "zones", but from increasing the layers of atoms, attracted by the action of the electrostatic field of atomic "ionization", i.e. filling the external shell of the atoms or, on the contrary, depriving electrons of the valence shell of an atom.
As shown, the given model does not need the presence of "conduction bands", but only the presence of "ions" in the locking layer.
Field (Zener) break-down
As described above when the strength of the electric field of the locked p-n junction becomes excessive, the value of the threshold of the electronic pairs originating from the external "ionized" shell of the atom, the field breakdown occurs. It will be wrong to name it "tunnel" break-down, since there is not any tunnel. That is only an imaginary concept within the framework of the artifact zonal theory.
In accordance with this, there is sharp ‘dog-leg’ in the volt-ampere characteristics of a locked junction. This is exactly how the Zener diode works, when voltage field breakdown is defined by the strength of the relationship between valence electrons in the locking layer of ions.
The results of experiments do not support the existing zonal theory which indicates that all junctions i.
å. - semiconductor are rectifying, regardless of the relative values of the work done on escaping. However within the framework of the proposed model it is easy to explain that the rigid characteristics of a junction do not depend on features of "zones", but from the presence of an "ionized" locking layer, which always appears when a transition from one type of conductivity to another exists. Moreover, it appears that even with a junction of one kind of conductivity, there exist conditions that make it possible for the removal of electrons from one material to the other, that is to say the complementing of "ionizing" valence shells.Avalanche break-down
Under even higher electric field strengths than the levels causing field breakdown, avalanche breakdown takes a place. This is where electronic pairs cascade, with the electrostatic field dislodging new pairs from atomic shells.
This explanation is not so different from the existing electronic theory apart from one essential detail. That is, the exceedingly small size of electronic pairs in pair-electronic conduction.
The possibility of forming exceedingly fine current cords and the consequent large power, is related to this property. Current cords, formed by the Ampere force, bring with them other interesting physical phenomena which cannot be unexplained from the standpoint of Fermi-Dirac-Schroedinger theories.
Now we will go to phenomena, which can not be explained by relativistic (ether-denial) and the logically twisted physics of the past.
Body-field break-down
Within the framework of the proposed model, it is natural to expect that high electric field strengths in the conductor or semiconductor must rip the electrons from the external shells of the atoms.
Actually, at an electric intensity of 106 [V/m] in silicon and 105 [V/m] in germanium, Ohms law ceases to apply [9] that is to say, a sharp increase in specific conductivity occurs. In metals, where the energy relationship between the electrons is far less, this phenomenon occurs at an electric intensity of 103 – 104 [V/m].
The observation of this effect is compounded by fact that before such a high level of electric field strength is reached, the conduction decays under the action of Joulian heat, released by the current. Is it possible to observe these phenomena in reality? Yes, it is! It is possible and was long ago observed in at least in three cases:
In reality, these three cases occur together, intensifying the effect of each other.
Let us consider some practical examples.
Tesla's Transformer [10-11]. More than 100 years ago, the genius inventor Nikola Tesla, created the high-voltage line of transmission of electrical energy, by which he sent, not withstanding Ohmic calculations, a much greater energy. The step-up transformer was the source of the high-voltage for this line.
A circuit of this kind drives short pulses of current into the load, the duration time of which is less than the life time of the electronic pairs. Besides, since the spectrum of frequencies of that line is very high, the main current is concentrated into a fine surface layer on the conductor, this increases the current density - of electric field intensity on the one hand, tap of Joulean heat from conducting surface - on the other hand. In other words, the relatively low temperature of the metal creates conditions of low electrical resistance within the skin of the metal where great currents may flow.
Golubev's spool of inductance [12]. Victor Golubev conducted experiments with radio-frequencies using spools of inductance having a high Q-factor. He found a large reduction in the ohmic resistance of the spool giving large resonance currents.
Avramenko Plug [13]. Stanislav Avramenko made a variant of Tesla's transformer, adding to it, a diode rectifier. This allowed him to get a greater pulsed current with a relatively low voltage of transformer. As this circuit is uncritical to ohmic resistance of line, that "violation of Ohm's Law" is observed. In other words when we create very short current pulses, referring to the resistance of a short electric line has no meaning, because electronic pairs have time to overcome the line distance without decay.
Explosive emission
If an electric field of large electric field strength is placed across a metal/vacuum interface, an explosive emission of electrons appears, characterizing very-large-scale 1012 - 1013 [A/m2] density of current over small areas.
Unexplained in terms of the "zonal theory" such a current density can appear with the interaction of electronic pairs of small size. Ampere force, i.e. force of magnetic field of the electric current itself form fine current cords consisting of electronic pairs. The density of current within it is such that it brings about a destruction of the electronic shells of the atoms in a small volume of the material. The Temperature of this volume rises almost instantly to values of several millions of degrees. Boiling and micro-explosions occur in the metal [14-22].
Electric Discharge Transmutation
If a current with a density of 1013 [A/m2] or higher flows through a material for a short time, then obviously, the electronic pairs of such a density can "strip" not only the valence shells, but also the internal electronic shells of an atom.
In this case, the atomic nucleus becomes "naked", and it is possible for nuclear reactions to occur, either with the fusing together of both nuclei, or the disintegration of the nucleus under the action of electronic pair flow, because the size of the electronic pair is equivalent to the size of a nucleon. Besides that, it will be natural electronic capture and even double electronic capture.
The employees of RNC "Kurchatov Institute" Urutskoev, Liksonov and Tsynoev [23] organized experiments on the study of electrical discharge explosions of titanium wire in sealed polyethylene balloons, filled by water.
As a result this experiment, new chemical elements were revealed, which had not been present at the installation.
Amongst these elements produced were Na, Ca, Fe, Ni, Au, Pb.
Conclusions
The analysis of electronic-wave and zonal electronic theories of Fermi - Dirac - Schrodinger have revealed discrepancies in describing the physical nature of conduction phenomena.
Proposed ethereal model of conduction adequately explains conduction in metals and the phenomena of superconductivity and provides explanations to the experiments of Nikola Tesla, S. Avramenko, V. Golubev, L. Urutskoev, V. Liksonov and V. Tsynoev.
The relationship between the critical temperature of superconductivity, specific heat and information measures of structured organization of material (as a described transformation factor D of the dynamic density), optical density and velocity of light in material, opens up a scientific alternative to a researcher seeking new superconductive materials.
The proposed theory makes clear the true nature of substances and confirms the existence of ethereal electrons.
Acknowledgement
The author expresses his gratitude to physicist Lyndon Ashmore (Dubai) for his suggestions for refining of the English version of this paper.
References
Karim Khaidarov