
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
А. Л. Дмитриев
Санкт-Петербург
2007
УДК 621. 382
А. Л. Дмитриев. Оптические системы передачи информации /Учебное пособие. - СПб: СПбГУИТМО, 2007. - 96 с.
В учебном пособии изложены основы оптических систем передачи информации. Рассмотрены элементы теории передачи информации, принципы построения открытых и волноводных оптических систем передачи сигналов, основы волноводной теории волоконно-оптических световодов, назначение и характеристики важнейших устройств оптической компонентной базы ВОСПИ, методы уплотнения информации, принципы действия когерентных и солитонных оптических систем передачи информации.
Учебное пособие предназначено для студентов старших курсов Инженерно-физического факультета СПбГУИТМО, обучающихся по направлению “Техническая физика” и специальностям “Лазерная техника и лазерные технологии”, “Физика и техника оптической связи.
Рекомендовано УМО по образованию в области приборостроения и оптотехники в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальности 200201 – “Лазерная техника и лазерные технологии”
Рисунки к учебному пособию выполнили студенты Инженерно-физического факультета А. Живага, Д. Терентьев, Н. Рыжаков,
Д. Багаветдинов, В. Федюков.
В 2007 году СПбГУ ИТМО стал победителем конкурса инновационных образовательных программ вузов России на 2007–2008 годы. Реализация инновационной образовательной программы “Инновационная система подготовки специалистов нового поколения в области информационных и оптических технологий” позволит выйти на качественно новый уровень подготовки выпускников и удовлетворить возрастающий спрос на специалистов в информационной, оптической и других высокотехнологичных отраслях экономики.
©
университет информационных технологий,
механики и оптики, 2007 г.
© А. Л. Дмитриев, 2007 г.
ОПТИЧЕСКИЕ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
Введение
Чем цивилизованнее и могущественнее перед силами природы человеческое общество, тем сильнее в нем развиты системы передачи и обработки информации. Аналогом человеческого общества является головной мозг: у низших живых организмов количество нейронов головного мозга (нейрон – элемент нервной системы или клетка, через которую происходит передача информации) существенно меньше и связи между ними развиты гораздо слабее, чем у человека. Именно поэтому человек превосходит все живые существа на Земле по приспособляемости, противостоянию внешней агрессии и творческим способностям. Перефразируя известное изречение Бэкона, кратко можно утверждать, что “информация” – это “сила”.
Развитые страны сегодня находятся в состоянии перехода от “индустриального” человеческого общества к “обществу информационному”, отличительная особенность которого состоит в создании и непрерывном усовершенствовании сложных “интеллектуальных сетей” – систем быстрого, эффективного и экономичного предоставления информационных
услуг массовому пользователю.Увеличение объема и скорости передачи информации в высокопроизводительных интеллектуальных сетях требует разработки соответствующих технических средств, среди которых оптика и оптические методы передачи сигналов играют важнейшую роль.
Уточнение и строгое определение понятия “информация” началось примерно с конца 40-х годов ХХ века, в связи с активным развитием кибернетики (от греческого “искусство управления”), то есть теории передачи и обработки информации, в работах Винера и Шеннона. В трудах Колмогорова, Эшби, Хартли и других исследователей информация обычно определяется как характеристика внутренней
организованности материальной системы. Соответственно, количество информации является мерой организованности (упорядоченности) такой системы, что указывает на ее связь с понятием энтропии физической системы.Информация – фактор, способствующий увеличению организованности, порядка в физической, химической, биологической, социальной и т. п. системах материальных тел. Одно из удачных определений (правильнее говорить, объяснений) понятия “информация” предложено Л. Бриллюэном. Допустим, в исходном положении физическая система имеет
 равновероятных состояний. Если о состоянии данной системы получены дополнительные сведения, то есть получена некоторая информация, при описании свойств физической системы число ее возможных равновероятных состояний уменьшается до величины
равновероятных состояний. Если о состоянии данной системы получены дополнительные сведения, то есть получена некоторая информация, при описании свойств физической системы число ее возможных равновероятных состояний уменьшается до величины  . При этом величина
. При этом величина  полученной информации, по определению, равна
полученной информации, по определению, равна
 . (1)
. (1)
В этом определении логарифмы введены для придания информации свойства аддитивности. Коэффициент
 определяет выбор единиц измерения информации. При
определяет выбор единиц измерения информации. При  размерность информации
размерность информации  называют “нат”, при
называют “нат”, при  - “бит”.
- “бит”.
В статистической термодинамике известна связь энтропии
 системы материальных частиц с термодинамической вероятностью
системы материальных частиц с термодинамической вероятностью  системы, равной числу возможных, тождественных с макроскопической точки зрения, состояний системы,
системы, равной числу возможных, тождественных с макроскопической точки зрения, состояний системы,
 (2)
(2)
(формула Больцмана), где постоянная Больцмана
 .
.
Сравнивая (1) и (2), приравняв условно коэффициенты
 , можно определить информацию и как фактор, способствующий уменьшению величины энтропии (беспорядка) физической системы,
, можно определить информацию и как фактор, способствующий уменьшению величины энтропии (беспорядка) физической системы,
 , (3)
, (3)
где
 и
и  соответственно энтропия начального и конечного (после получения информации
соответственно энтропия начального и конечного (после получения информации  о системе) состояний.
о системе) состояний.
Следует отметить, что принятое в современной статистической теории понятие “информация” исключает, намеренно игнорирует характеристику ценности информации. Это положение иллюстрируется примером, что 100 букв в стихотворении гениального поэта содержит ровно столько же информации, сколько 100 букв в заурядном газетном репортаже. Формулировка критерия ценности информации является отдельной, довольно сложной задачей.
Информация в энергетической, действующей форме реализуется в виде сигналов. “Сигнал” – это физический процесс (электрический, акустический, электромагнитный и др.), несущий сообщение. “Сообщение” есть совокупность сигналов, содержащих информацию. “Данные” есть информация в формализованном виде, позволяющем регистрировать ее на физическом носителе и осуществлять обработку и передачу информации с помощью технических средств.
Теория информации на основе различных статистических (вероятностных) моделей процесса передачи информации позволяет сформулировать оптимальные способы преобразования и обработки сигналов для их наиболее достоверного воспроизведения в оконечном устройстве системы источник – получатель информации.
Общая схема системы передачи информации показана на рис. 1.
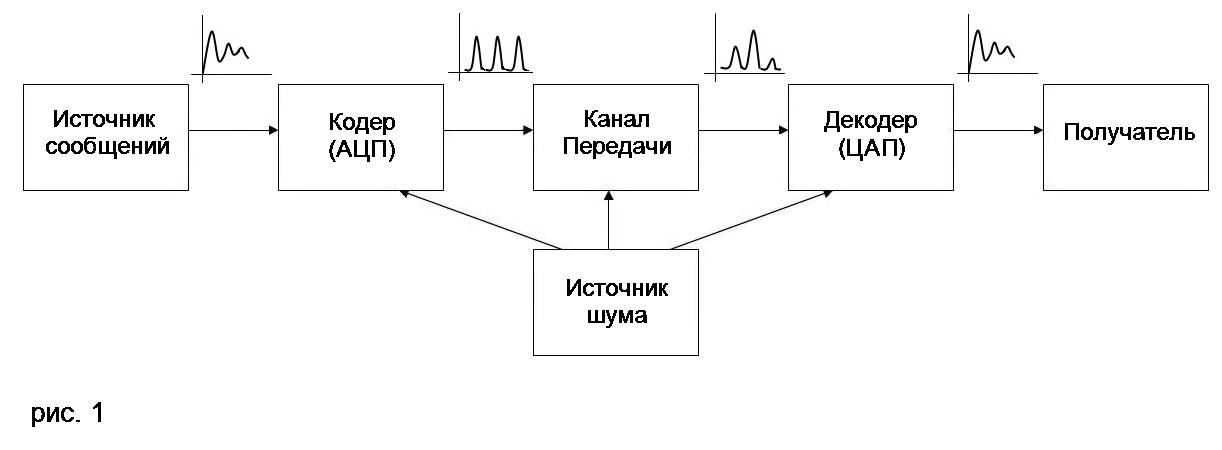
Рис. 1. Общая схема системы передачи информации
Процесс передачи информации неизбежно сопровождается различными случайными дестабилизирующими воздействиями, то есть шумами. Создание системы передачи сигналов, устойчивой к влиянию шумов различной природы (аддитивных, мультипликативных и др.), и является основной задачей разработчиков таких систем, при этом существенную роль играет выбор способа кодирования сигналов, распространяющихся в канале передачи. Одним из главных следствий современной теории информации является утверждение
, что наиболее достоверное воспроизведение сигнала на выходе системы передачи обеспечивается именно при дискретном (“цифровом”) кодировании сигналов. При определенных требованиях к дискретному преобразованию сигналов в оконечном устройстве системы на Рис. 1 можно восстановить входную последовательность сигналов с любой точностью.Скорость
 передачи информации равна отношению объема
передачи информации равна отношению объема  переданной информации к времени
переданной информации к времени  передачи,
передачи,
 . (4)
. (4)
Теорема Шеннона показывает зависимость скорости передачи информации от технических характеристик системы передачи – ширины
 полосы передаваемых частот и отношения сигнал/шум (
полосы передаваемых частот и отношения сигнал/шум ( ) в оконечном устройстве этой системы,
) в оконечном устройстве этой системы,
 , (5)
, (5)
где
S/N – отношение среднеквадратической мощности сигнала к среднеквадратической мощности шума на выходе системы передачи. Очевидно, пропускающая способность системы передачи информации прямо пропорциональна ширине полосы частот передачи. Например, в телефонии при передаче аналогового звукового сигнала величина
полосы частот передачи. Например, в телефонии при передаче аналогового звукового сигнала величина  = 8 кГц, а при передаче этого телефонного сигнала в цифровой форме, при 8 знаках двоичного кода (соответствующих 256 уровням квантования величины сигнала), полоса частот передачи в 8 раз шире,
= 8 кГц, а при передаче этого телефонного сигнала в цифровой форме, при 8 знаках двоичного кода (соответствующих 256 уровням квантования величины сигнала), полоса частот передачи в 8 раз шире,  =64 кбит/с. Аналоговый аудио-сигнал имеет полосу частот
=64 кбит/с. Аналоговый аудио-сигнал имеет полосу частот  =22.05 кГц и для его высококачественной цифровой передачи, при 16 разрядах в двоичном коде, требуется полоса частот
=22.05 кГц и для его высококачественной цифровой передачи, при 16 разрядах в двоичном коде, требуется полоса частот  =2.03 Мбит/с. Обычное ТВ-изображение переносится аналоговым сигналом в полосе частот
=2.03 Мбит/с. Обычное ТВ-изображение переносится аналоговым сигналом в полосе частот  =4 МГц, а при 256 уровнях квантования величины сигнала
=4 МГц, а при 256 уровнях квантования величины сигнала  =32 Мбит/с. Полоса частот передачи в цифровом телевидении высокой четкости (ТВЧ) равна 504.3 Мбит/с.
=32 Мбит/с. Полоса частот передачи в цифровом телевидении высокой четкости (ТВЧ) равна 504.3 Мбит/с.
Эта теорема определяет необходимые условия дискретного преобразования (кодирования) сигналов, при котором выборочные значения сигнала содержат полную информацию о сигнале в любой момент времени.
Если задана периодическая функция
 , где
, где  и
и 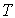 - период, с ограниченным (максимальная угловая частота спектра равна
- период, с ограниченным (максимальная угловая частота спектра равна ) фурье-спектром, она представляется конечным рядом Фурье
) фурье-спектром, она представляется конечным рядом Фурье
 , (6)
, (6)
где
 и
и  коэффициенты Фурье,
коэффициенты Фурье,  и
и  . Можно показать, что такая функция представляется рядом ее выборочных значений с весовыми коэффициентами вида функций отсчетов (
. Можно показать, что такая функция представляется рядом ее выборочных значений с весовыми коэффициентами вида функций отсчетов ( ),
),
 , (7)
, (7)
где период выборки
 ;
;  - максимальная частота спектра сигнала, измеренная в Гц (
- максимальная частота спектра сигнала, измеренная в Гц ( ). Видно, что непрерывная функция с ограниченным спектром (“финитная” функция) полностью определяется ее выборочными значениями
). Видно, что непрерывная функция с ограниченным спектром (“финитная” функция) полностью определяется ее выборочными значениями  в дискретных точках, кратных интервалу выборки
в дискретных точках, кратных интервалу выборки  . На основании (7) теорема Шеннона-Котельникова утверждает: передача непрерывной функции может быть сведена к передаче ее отдельных выборочных значений (отсчетов) или кодовых комбинаций, содержащих информацию о величине отсчетов, с тактовой частотой не менее, чем
. На основании (7) теорема Шеннона-Котельникова утверждает: передача непрерывной функции может быть сведена к передаче ее отдельных выборочных значений (отсчетов) или кодовых комбинаций, содержащих информацию о величине отсчетов, с тактовой частотой не менее, чем  .
.
Точный вид функции
 в любой момент времени восстанавливается по ее выборочным значениям
в любой момент времени восстанавливается по ее выборочным значениям  при умножении величин выборок на соответствующие функции отсчетов (вида
при умножении величин выборок на соответствующие функции отсчетов (вида  ) и суммировании достаточно большого числа членов бесконечного ряда (7). Это поясняет
) и суммировании достаточно большого числа членов бесконечного ряда (7). Это поясняет
рис. 2.

Рис. 2. Иллюстрация теоремы отсчетов. Нули функций отсчетов совпадают с моментами отсчетов.
Для полного дискретного представления сигналов (и соответствующей “цифровой” их передачи по каналу связи) недостаточно выполнить отсчеты значений сигналов в дискретные моменты времени, кратные
 . Необходимо представить также в дискретном виде (кодировать) величину каждого сигнала выборки и обеспечить ее передачу. Это достигается квантованием уровня (величины) этих сигналов с последующим представлением их в удобном для импульсной передачи двоичном коде.
. Необходимо представить также в дискретном виде (кодировать) величину каждого сигнала выборки и обеспечить ее передачу. Это достигается квантованием уровня (величины) этих сигналов с последующим представлением их в удобном для импульсной передачи двоичном коде.
Принцип импульсно-кодовой модуляции (ИКМ) поясняется на рис. 3.

Рис. 3. Принцип ИКМ. а. – аналоговый непрерывный сигнал, б – квантование выборочных значений (отсчетов) сигнала, в – представление выборочных значений в двоичном коде.
Дискретное представление (квантование) уровня сигналов предварительно осуществляется в десятичном коде с последующим его представлением в двоичном коде. В Таблице 1. показан пример такого перехода от десятичного к двоичному коду.
Таблица 1.
|
Значение выборки в десятичном коде |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Двоичное значение |
0 |
1 |
10 |
11 |
100 |
101 |
110 |
|
Число ( |
1 |
1 |
2 |
2 |
3 |
3 |
3 |
Число ![]() уровней шкалы квантования сигнала определяется числом
уровней шкалы квантования сигнала определяется числом ![]() разрядов (знаков) в двоичном коде,
разрядов (знаков) в двоичном коде, ![]() . Для цифрового кодирования сигналов в телефонии часто принимается
. Для цифрового кодирования сигналов в телефонии часто принимается ![]() , что соответствует 256 уровням квантования сигнала выборки.
, что соответствует 256 уровням квантования сигнала выборки.
При ИКМ величина сигнала выборки в двоичном коде передается в канале связи непосредственно с момента каждой выборки, а для параллельной (одновременной) передачи сигналов нескольких каналов используется принцип временного уплотнения – деления тактового интервала  на отрезки времени, каждый из которых придан определенному каналу. Указанные преобразования исходного сигнала осуществляются в электронном аналого-цифровом преобразователе (кодере, АЦП) и далее в специальной аппаратуре временного уплотнения (временного мультиплексирования) сигналов. Пример организации 30-канальной ИКМ, обеспечивающей одновременную трансляцию 30 телефонных каналов, показан на рис. 4. Здесь тактовый интервал (период выборки)
на отрезки времени, каждый из которых придан определенному каналу. Указанные преобразования исходного сигнала осуществляются в электронном аналого-цифровом преобразователе (кодере, АЦП) и далее в специальной аппаратуре временного уплотнения (временного мультиплексирования) сигналов. Пример организации 30-канальной ИКМ, обеспечивающей одновременную трансляцию 30 телефонных каналов, показан на рис. 4. Здесь тактовый интервал (период выборки)  телефонного звукового сигнала равен 125 мкс и определен граничной частотой
телефонного звукового сигнала равен 125 мкс и определен граничной частотой  этого сигнала, условно равной 4 кГц (
этого сигнала, условно равной 4 кГц ( ).
).
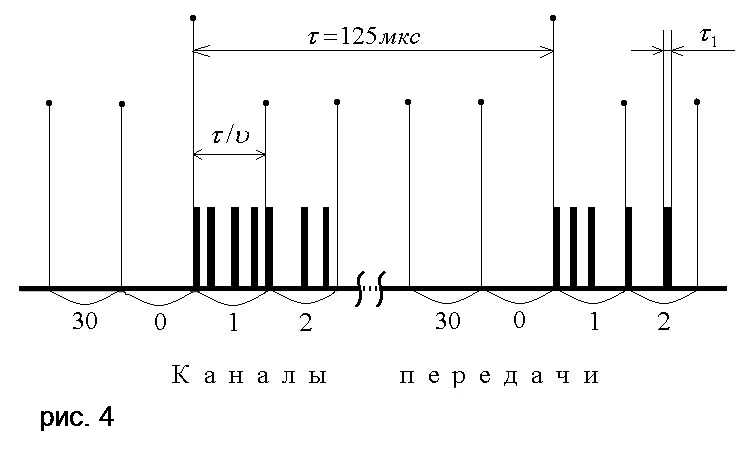
Рис. 4. Принцип построения ИКМ-30. 31-й (нулевой) канал – канал синхронизации.
Длительность
![]() , (8)
, (8)
где
Отличительной особенностью цифровых систем передачи является их сравнительно малая чувствительность к воздействию шумов и помех. Передаваемый по оптической линии связи цифровой сигнал часто имеет два дискретных значения (“0” и “1”), а фотоприемное устройство (ФПУ) работает в пороговом режиме как логическое устройство с двумя выходными состояниями – “да” и “нет”, и даже при значительных искажениях амплитуды принимаемого сигнала на выходе ФПУ двоичные сигналы имеют правильную форму. Электронный цифро-аналоговый преобразователь (декодер, ЦАП), на вход которого подаются сигналы ФПУ, осуществляет высококачественное восстановление исходного аналогового сигнала.
Понятие спектра сигнала в физике тесно связано с преобразованием Фурье, согласно которому “хорошая” (ограниченная, дифференцируемая и не имеющая разрывов) функция
 . (9)
. (9)
Спектральная функция
 . (10)
. (10)
Смысл выражения (9) состоит в представлении функции
Если сигнал
 . (11)
. (11)
Дельта-функция (здесь - “спектр” монохроматического сигнала) отлична от нуля лишь в точке

Рис. 5. Монохроматический сигнал (а) и его спектр (б)
Спектральная функция модулированного по амплитуде сигнала, например, меандра с длительностью цуга равной

Рис. 6. Меандр (а) и его спектр (б)
Определенная по условному критерию (например, по уровню 0.8 от максимального значения квадрата модуля спектральной функции) ширина спектра
![]() . (12)
. (12)
Соотношение 12 приблизительно, по порядку величины, выполняется и при других видах амплитудной модуляции сигнала, например, с огибающей в виде функции Гаусса либо в виде экспоненты с линейным по времени показателем; при этом
 . (13)
. (13)
В современной теории информаци определение понятия “спектр сигнала” основано на понятии функции автокорреляции, являющейся одной из главных статистических характеристик случайного процесса. Реальные сигналы никогда не бывают строго детерминированными и, вообще говоря, описываются случайными функциями

Рис. 7. Случайный процесс
Автокорреляционная функция
 , (14)
, (14)
где интервал усреднения
 , (15)
, (15)
где спектральная функция (спектр) случайного процесса
 . (16)
. (16)
Пару фурье-преобразований (15, 16), где


Рис. 8. Примеры автокорреляционных функций (а) и соответствующих спектров (б) различных случайных процессов
Так как для физически осуществимых процессов автокорреляционная функция
 , (17)
, (17)
 , (18)
, (18)
где нормированная функция автокорреляции равна
При передаче информации с использованием сигналов электромагнитных волн нередко требуется выполнение условия квазимонохроматичности, согласно которому ширина
![]()
![]() . (19)
. (19)
Так как ширина
Вторая особенность оптического диапазона связи – необходимость учета квантовых свойств излучения, которые проявляются как при генерации излучения, так и при его регистрации фотоприемниками (то есть при взаимодействии излучения со средой). Фотоны (кванты излучения, бозоны) в квантовой электродинамике описываются симметричными волновыми функциями, следовательно, как частицы с целым спином подчиняются статистике Бозе-Эйнштейна. В этой статистике среднее число фотонов
 , (20)
, (20)
где
число фотонов в квантовом состоянии велико,
Средние квадраты флуктуаций числа фотонов, равные, по определению,
![]() , (21)
, (21)
(здесь предполагается усреднение по времени) существенно различны в СВЧ- и в оптическом диапазоне волн. В диапазоне СВЧ преобладают тепловые шумы, при этом
![]() , (22)
, (22)
и относительная величина флуктуаций числа фотонов
![]() ; (23)
; (23)
такой тип флуктуаций числа фотонов соответствует классической статистике Пуассона. Энергия
![]() . (24)
. (24)
В оптическом диапазоне выполняется
![]() , (25)
, (25)
при этом относительная величина флуктуаций числа фотонов существенно выше,
![]() . (26)
. (26)
Энергия шума
![]() , (27)
, (27)
что намного больше величины
В открытых оптических системах связи свет распространяется в свободной среде - в атмосфере либо в космическом пространстве. Принципиальная схема таких систем передачи сигналов приведена на рис. 9.

Рис. 9. Открытая оптическая система связи. 1 – источник света, 2 и 3 – объективы, 4 – фотоприемник
.При учете только дифракционных эффектов расходимости света мощность
 , (28)
, (28)
где
Коэффициент пропускания атмосферы равен
![]() , (29)
, (29)
где коэффициент
![]() . (30)
. (30)
Коэффициент поглощения
![]() . (31)
. (31)
Рассеяние Релея есть рассеяние света на частицах, размеры которых намного меньше длины световой волны, и его влияние наиболее заметно в области коротких длин волн,
 , (32)
, (32)
где
Эмпирическая формула для коэффициента рассеяния Ми (рассеяния на частицах размерами намного большими, чем
 , (33)
, (33)
где
Очевидно, на дальность (и надежность) открытых систем связи в атмосфере заметно влияют метеорологические условия: туман, дождь, снег, дым, турбулентность атмосферы и др. Для больших расстояний
Исторически первая оптическая волноводная система передачи информации (Губо и Шверинг, 1961 г.) была выполнена на основе конфокального линзового волновода, схема которого приведена на рис. 10.

Рис. 10. Ход лучей света в конфокальном линзовом волноводе
Линзовый волновод (ЛВ) представляет собой набор положительных линз, последовательно расположенных на двойном фокусном расстоянии (практически - величиной около 1 метра). Назначение линз – компенсировать дифракционную расходимость оптического излучения в волноводе. Основные недостатки ЛВ – необходимость точной (с точностью около 20 мкм) установки расстояний между линзами, сравнительно большие
(примерно 100 дБ/км) оптические потери ЛВ и дороговизна. Тем не менее, скорость передачи сигналов в таком линзовом волноводе приближалась с скоростям передачи радиорелейных линий связи.
В газо-линзовом волноводе (рис. 11) (Барреман, 1964 г.), благодаря высокой температуре стенок волновода, распределение температуры (и плотности) газа в сечении волновода неоднородно и в центре волновода показатель преломления газа выше, чем у стенок газовой трубы.

Рис. 11. Устройство газо-линзового волновода
Вследствие рефракции, световые лучи концентрируются вблизи оси волновода. Для поддержания рабочего режима такого волновода энергозатраты на нагревание стенок достаточно велики и поэтому газо-линзовые световоды не нашли широкого применения.
Аналогом СВЧ-волноводов являются трубчатые оптические волноводы (лучеводы). Такие волноводы представляют собой пустотелые трубки из стекол либо металлов с зеркальным покрытием внутренней поверхности, с диаметром отверстий порядка мм. Лучеводы не нашли практического применения в оптической связи и сегодня частично используются в лазерной технологии для канализации мощных потоков оптического излучения.
5.1
. Классификация волоконных световодовПростой волоконный световод (ВС) представляет собой структуру из двух коаксиальных цилиндров – сердцевину с показателем преломления

а.
б. в.Рис. 12 . Профиль показателя преломления ВС. а – многомодового, б – одномодового, в – градиентного.
Диаметр оболочки ВС обычно равен 125 мкм (иногда 30, 200, 400 мкм) , радиус
Ход светового луча в меридиональной (содержащей оптическую ось) плоскости ВС показан на Рис. 13.

Рис. 13. Ввод луча света в одножильный волоконный световод
Критический (наименьший) угол

![]() , (34)
, (34)
а для соответствующих наибольших углов падения
![]() , (35)
, (35)
где
 . (36)
. (36)
Типичные значения параметров наиболее распространенных ВС приведены в Таблице 2.
Таблица 2.
|
Тип световода (кварцевое стекло) |
Диаметр сердцевины, мкм |
|
|
|
|
Многомодовый |
50 - 200 |
0.25 – 0.50 |
20 - 30 |
0.005-0.020 |
|
Одномодовый |
5 – 12 |
0.12 – 0.25 |
5 - 8 |
0.002-0.010 |
Для достижения улучшенных характеристик дисперсии ВС разработано несколько типов ВС со сложным профилем показателя преломления, примеры которых показаны на рис. 14.


Рис. 14. Волоконные световоды со сложными профилями показателя преломления. а – четырехслойный ВС, б - градиентный.
В оптических приборах нередко применяются однородные кварцевые световоды с пластиковой оболочкой и полимерные, полностью изготовленные из полимерных материалов, световоды. Как правило, они отличаются большой величиной числовой апертуры (0.3 – 0.5), большим диаметром сердцевины (150-200 мкм), а по параметрам дисперсии и оптических потерь значительно уступают лучшим образцам ВС.
В волоконно-оптических гироскопах и в волоконных интерферометрах используются световоды с сохранением поляризации излучения.
В таких одномодовых световодах необходимая оптическая анизотропия сердцевины оптоволокна достигается вследствие эффекта фотоупругости. Различие упругих механических напряжений вдоль ортогональных направлений (

Рис. 15. ВС с сохранением поляризации. а – с эллиптической напрягающей оболочкой, б – типа “
PANDA”, в – типа “галстук-бабочка”.
Итак, волоконные световоды обычно подразделяются на одномодовые, многомодовые, градиентные, ВС с сохранением поляризации и ВС со сложным профилем показателя преломления (к ним относятся ВС с несколькими световодными жилами, ВС с некруглой сердцевиной, а также “дырчатые”, микроструктурированные ВС).
Требуемое значение показателя преломления сердцевины или оболочки волоконного световода обеспечивается введением в чистый плавленый кварц (двуокись кремния -

Рис. 16. Зависимость показателя преломления кварцевого стекла от концентрации примесей (длина волны 850 нм).
Профиль показателя преломления в ВС определяется технологией изготовления волокна. Старым методом двойного тигля в 80-е годы удалось получить оптоволокно с потерями величиной 2-8 дБ/км. Световоды высшего качества получены по принципиально новой технологии, разработанной в
70-е годы. Сущность такой технологии состоит в изготовлении, на первом этапе, крупногабаритного стеклянного стержня-заготовки с требуемым радиальным распределением показателя преломления и - на втором этапе - вытяжке оптоволокна при нагревании этой заготовки выше температуры плавления стекла (около 1400 С). Первое время при изготовлении заготовок практиковался метод наружного осаждения окислов металлов из газовой фазы на поверхность стержня из графита (
Outside Vapor Phase Oxidation – “OVPO”). Сегодня наиболее распространен метод внутреннего осаждения из газовой фазы (Modified Chemical Vapor Deposition – “MCVD”). Сущность MCVD-метода состоит в последовательном, по специальному алгоритму, осаждении на внутренней поверхности вращающейся и нагреваемой кварцевой трубки продуктов сгорания (окислов) различных веществ, после чего полученная таким способом пористая заготовка разогревается до температуры стеклования – образования прозрачного стекла. Оптические потери в ВС, полученных методом MCVD, достигают уровня 0.2 дБ/км на длине волны 1.55 мкм. Еще лучшие результаты, особенно в области длин волн около 1,3 мкм, получены при изготовлении заготовок в вакууме с использованием метода торцевого осаждения (Vapor Phase Axial Deposition – “VAD”). Из одной монолитной стеклянной заготовки длиной около 1 метра и диаметром 10-15 мм можно вытянуть до 50 км градиентного (или многомодового) волокна и свыше 100 км – одномодового волокна.Оптические потери в линиях связи (и в световодах) удобно исчислять в дБ/км. Если на входе линии протяженностью
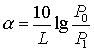
Коэффициент потерь
![]() ; (38)
; (38)
(здесь размерность коэффициента поглощения
Следует отметить, что при очень высоких плотностях мощности оптического излучения в кварцевом световоде - более
Характерными особенностями релеевского рассеяния света являются примерно равное рассеяние в прямом и обратном направлениях, линейная поляризация рассеянного в сторону излучения и сильная, пропорциональная
Потери вследствие фундаментального поглощения излучения в стекле обусловлены тремя механизмами: собственным поглощением материала, поглощением на примесях (несобственным поглощением) и потерями на дефектах атомной решетки. Мощное собственное поглощение вызывается электронными переходами в ультрафиолетовой (УФ) области спектра и переходами между колебательными уровнями в инфракрасной (ИК) области спектра системы энергетических уровней молекулы кварца (
Несобственное (примесное) поглощение значительно даже при очень низких концентрациях примесей, что иллюстрирует Таблица 3.
Таблица 3.
|
Примесь в |
Длина волны, мкм |
Вносимые потери, дБ/км |
|
|
1.10 |
0.68 |
|
|
0.40 |
0.15 |
|
|
0.85 |
1.10 |
|
|
0.95 1.38 1.24 |
1.00 20.00 4.00 |
Отмеченные в таблице сильные линии поглощения молекулы гидроксила (
Типичная спектральная зависимость оптических потерь в ВС, полученном по методу
MCVD, показана на рис. 17.

Рис. 17. Спектральная характеристика оптических потерь в кварцевом световоде, изготовленном по методике
MCVDВидно, что присутствие молекул воды (гидроксильных групп) в кварцевом стекле, приводит к значительным оптическим потерям на поглощение в области около 1.3 мкм.
При изготовлении заготовок для вытяжки оптоволокна методом торцевого осаждения в вакууме (
VAD) концентрация примеси
Рис.18. Спектральная характеристика оптических потерь в кварцевом оптоволокне, изготовленном по методу
VADАбсолютный минимум оптических потерь в одномодовом кварцевом световоде составляет примерно 0.125 дБ/км на длине волны 1.55 мкм. Минимальное затухание на длине волны 0.85 мкм около 2.5 дБ/км, на длине волны 1.3 мкм – около 0.35 дБ/км.
Дефекты оптоволокна – микронеоднородности плотности (следовательно, и показателя преломления) направляющей среды, трещины, свили, пузырьки, инородные частицы и т. п. обусловливают рефракцию и рассеяние излучения в волноводе. Соответствующие радиационые потери могут быть уменьшены при использовании высокочистых исходных материалов при изготовлении заготовок оптоволокна, а также эффективных современных технологий
MCVD, VAD, специальных режимов вытяжки волокна и др.Изгиб волокна приводит к нарушению условия полного внутреннего отражения на границе сердцевина-оболочка световода, в результате чего часть излучения переходит из сердцевины в оболочку и потери направляемых мод возрастают. При радиусе изгиба волокна менее критического, резко увеличиваются радиационные потери
![]() , (39)
, (39)
где
Сегодня исследуются и разрабатываются волоконные световоды на основе различных некварцевых стекол, например, фторидных и халькогенидных стекол, кристаллов галогенидов и ряда других материалов. В диапазоне длин волн свыше 2 мкм (например, около 6 и 8 мкм) в таких средах потери оптической мощности, вследствие фундаментального поглощения, достигают уровня 0.010 – 0.001 дБ/км. Серьезной проблемой практического применения таких сред является дороговизна исходных материалов
, сложности технологии их изготовления и неизбежные радиационные потери из-за оптической неоднородности материала световода, которые могут превышать потери на поглощение.5.4.
Волновая теория распространения излучения в волоконных световодахПри описании свойств волоконных световодов используется как геометрическое (лучевое), так и волновое приближения. Более точное описание характеристик ВС дает волновая теория, рассматривающая свет как распространение различных типов электромагнитных волн в цилиндрических диэлектрических волноводах. Основные положения этой теории были установлены еще в 40-50-е годы при анализе свойств СВЧ-волноводов.
Электромагнитное поле описывается системой уравнений Максвелла, из которой непосредственно следуют волновые уравнения для электрической и магнитной составляющих поля. В диэлектрической (плотность свободных зарядов равна нулю) среде волновые уравнения для величин электрического (
 , (40)
, (40)
 , (41)
, (41)
где
![]() (42)
(42)
и
![]() , (43)
, (43)
где
 , (44)
, (44)
где
 , (45)
, (45)
и

Рис. 19. Проекции электрического вектора э.м. поля в цилиндрической системе координат.
Общее решение волновых уравнений 40,41 в цилиндрической системе координат имеет вид волн, распространяющихся в положительном направлении оси
![]() , (46)
, (46)
![]() , (47)
, (47)
где
Волновые уравнения для проекций векторов поля имеют вид
 , (48)
, (48)
 , (49)
, (49)
 , (50)
, (50)
 . (51)
. (51)
В этих формулах параметр
 . (52)
. (52)
Из 48-51 прямо следуют два уравнения для продольных компонент электрической
 , (53)
, (53)
 . (54)
. (54)
Волновые уравнения 53,54 при заданных граничных условиях описывают распространение электромагнитных волн в диэлектрических волноводах с любым профилем показателя преломления.
5.4.2. Волновод со ступенчатым профилем показателя преломления и бесконечным радиусом оболочки
Волновые уравнения 53,54 имеют точные решения лишь в исключительных случаях, одним из которых является задача о распространении электромагнитной волны в прямом волноводе в виде однородного сплошного цилиндра (сердцевины) радиуса

Рис. 20. Профиль показателя преломления простейшего диэлектрического волновода
Решение волновых уравнений, например для
![]() , (55)
, (55)
где
 . (56)
. (56)
Это уравнение - хорошо изученное дифференциальное уравнение Бесселя, решениями которого являются специальные функции Бесселя
 , (57)
, (57)
а при больших значениях аргумента выполняется
 , (58)
, (58)
то есть асимптотически функция Бесселя – гармоническая, с медленно убывающей амплитудой.
Примеры графиков функций Бесселя показаны на рис. 21

Рис. 21. Функции Бесселя порядка
Решениями волновых уравнений могут являться функции Кельвина
![]() , (59)
, (59)
которые в отличие от осциллирующих функций Бесселя являются монотонно-убывающими. График функций Кельвина приведен на рис. 22.

Рис. 22. Функции Кельвина порядка
Решения волновых уравнений 53,54 различаются для сердцевины и оболочки волновода.
Для сердцевины волновода, в области
![]() , (60)
, (60)
![]() . (61)
. (61)
Для оболочки волновода, при
![]() , (62)
, (62)
![]() , (63)
, (63)
В равенствах 60-63 коэффициенты
![]() , (64)
, (64)
где
![]() , (65)
, (65)
где
Постоянная распространения
![]() . (66)
. (66)
Величина коэффициентов
![]() , (67)
, (67)
![]() . (68)
. (68)
Для азимутальных компонент поля граничные условия при
( ![]()
 , (69)
, (69)
 . (70)
. (70)
Уравнения 67-70 образуют систему четырех алгебраических уравнений с четырьмя неизвестными
 . (71)
. (71)
Это уравнение, которое определяет допустимые значения постоянной распространения
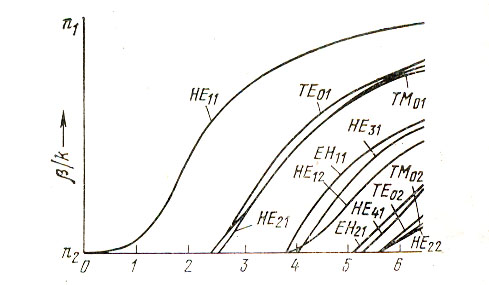
Рис. 23. Зависимость постоянной распространения (отношения
Здесь нормированная частота (или
![]() . (72)
. (72)
Основной моде волновода соответствуют наименьшие значения индексов мод

Рис. 24. Распределение силовых линий и векторов электрического поля в поперечном сечении волновода для мод низших порядков
При
![]() . (73)
. (73)
При сравнительно больших значениях
![]() ; (74)
; (74)
в этой формуле учтены два ортогональных состояния поляризации каждой из мод.
5
.4.3. Волоконные световоды с градиентным профилем показателя преломления
Функция

и
![]()
Здесь

Рис. 25 Профили показателей преломления градиентных ВС.
Числовая апертура градиентных световодов зависит от радиуса точки наблюдения, при этом в области
 . (77)
. (77)
Волновое уравнение для радиальной функции
 , (78)
, (78)
где
![]() , (79)
, (79)
после чего получаем уравнение для неизвестной функции
 . (80)
. (80)
Полагая, что
![]() . (81)
. (81)
Ограничившись первыми двумя членами в разложении 81, подстановкой их в 80, получим
 . (82)
. (82)
Слагаемые в фигурной и круглой скобках приблизительно равны нулю, откуда следует решение
 . (83)
. (83)
Волноводные моды в градиентном световоде распространяются внутри световода, если подкоренное выражение в 83 положительно, в противном случае мнимая функция
![]() , (84)
, (84)
где радиальный индекс моды (число полупериодов между точками поворота лучей) принимает значения

Рис. 26. Проекция траекторий световых лучей в поперечном сечении градиентного световода
Можно показать, что число мод
 . (85)
. (85)
Наибольшее число
 (86)
(86)
и при
Очевидно, параметр профиля
![]()
 . (87)
. (87)
Число мод градиентного световода всегда меньше, чем у ступенчатого световода с тем же радиусом сердцевины (например, при
5.4.4. Поток мощности излучения в волоконном световоде
Плотность потока мощности электромагнитного излучения описывается комплексным ветром Пойнтинга
![]() , (88)
, (88)
а проекция
![]() , (89)
, (89)
где
Можно показать, что
![]() . (90)
. (90)
Рассчитаем потоки электромагнитной энергии в сердцевине (

Рис. 27. Геометрия поперечного сечения ступенчатого световода. 1 – сердцевина, 2 – оболочка ВС
.Поток
 , (91)
, (91)
а поток
 . (92)
. (92)
Полный поток
![]() . (93)
. (93)
Относительная доля мощности излучения, переносимого сердцевиной прямого ступенчатого световода с бесконечным радиусом оболочки, рассчитывается на основе формул 90 и 60-72, при этом выполняется
 . (94)
. (94)
Графики зависимости относительной мощности излучения, переносимого сердцевиной и оболочкой световода, от нормированной частоты световода показаны на рис. 28.

Рис. 28. Зависимость относительной доли мощности в сердцевине (
Характерно, что при малых значениях
 , (95)
, (95)
где
Следовательно, относительная доля энергии излучения, переносимого оболочкой световода, уменьшается с ростом нормированной частоты
Деформации, в том числе изгиб волокна сопровождаются нарушением условия полного внутреннего отражения на границе сердцевина-оболочка оптоволокна и как следствие “перекачкой” энергии излучения от волноводных к оболочечным (излучательным) модам. Этот процесс наиболее активен для мод высокого порядка. В изогнутом световоде расчет параметров волноводных мод и условий их распространения довольно сложен, здесь необходимо также принимать во внимание вызванное деформациями ВС явление фотоупругости. Известна приближенная формула оценки эффективного числа
 . (96)
. (96)
Уменьшение радиуса изгиба волокна обусловливает уменьшение числа волноводных мод и, следовательно, увеличение оптических потерь в световоде. В частном случае прямого (
 . (97)
. (97)
Для ступенчатого (
Дисперсия (с латинского – рассеяние) в оптической связи означает уширение передаваемого импульсного сигнала, то есть увеличение его длительности. Явление дисперсии является одним из главных факторов, ограничивающих скорость передачи информации в линиях связи. Энергия излучения переносится в пространстве с групповой скоростью
 , (98)
, (98)
где
 . (99)
. (99)
В одномодовых световодах явление дисперсии носит сильно выраженный хроматический, то есть зависящий от длины световой волны, характер. В многомодовых световодах основной причиной дисперсии является различие постоянных распространения различных волноводных мод, в результате которого групповые задержки разных мод даже на одной длине волны значительно различаются.
Многомодовые световоды
Для световода со ступенчатым профилем показателя преломления удобно ввести нормированную постоянную распространения
 . (100)
. (100)
При
![]() . (101)
. (101)
Групповая задержка
 , (102)
, (102)
где
Параметр групповой задержки
 . (103)
. (103)
Эта расчетная зависимость показана на рис. 29.

Рис. 29. Зависимость параметра групповой задержки от нормированной частоты волновода
Видно, что определенному значению
В многомодовом световоде величину групповой задержки, приблизительно равную уширению передаваемого импульсного сигнала (межмодовую дисперсию), нередко оценивают по формуле
 . (104)
. (104)
Одномодовые световоды
В одномодовых световодах полная величина дисперсии равна алгебраической сумме волноводной (“внутримодовой”) дисперсии и материальной дисперсии. При этом длина волны и ширина спектра направляемого излучения играет существенную роль.
Коэффициент дисперсии ![]() , по определению, равен изменению величины групповой задержки (выраженной, например, в нано- или пикосекундах) на единицу длины линии (обычно на 1 км) при изменении длины волны передаваемого сигнала (на 1 нм),
, по определению, равен изменению величины групповой задержки (выраженной, например, в нано- или пикосекундах) на единицу длины линии (обычно на 1 км) при изменении длины волны передаваемого сигнала (на 1 нм),
 . (105)
. (105)
Размерность дисперсии часто выбирают равной
 .
.
При известной величине
![]() . (106)
. (106)
Подставляя 99 в 105, получим
 . (107)
. (107)
Материальная дисперсия
Постоянная распространения плоской волны в дисперсной среде равна
![]() , (108)
, (108)
где
 (109)
(109)
и, очевидно, прямо зависит от длины волны излучения. Зависящая только от свойств материала дисперсия (“материальная дисперсия”)
 . (110)
. (110)
Кварцевое стекло, являющееся наиболее распространенным материалом волоконных световодов, в ближней ИК-области длин волн имеет характерную спектральную зависимость показателя преломления с точкой перегиба на длине волны 1.27 мкм – рис. 30.а.

Рис. 30. а. – спектральная зависимость показателя преломления чистого кварцевого стекла. б – спектральная зависимость материальной дисперсии в кварцевом стекле.
В этой же точке материальная дисперсия
Внутримодовая дисперсия
Внутримодовая дисперсия
 . (111)
. (111)
В общем случае, внутримодовая дисперсия имеет место для любой из мод волновода, включая моды высокого порядка.
Подставляя выражения 102, 103 в 111, полагая показатель преломления
 . (112)
. (112)
Полная дисперсия
![]() . (113)
. (113)
В кварцевых одномодовых световодах (при

Рис. 31. Спектральные зависимости волноводной (1), материальной (2) и полной (3) дисперсий в одножильном оптическом световоде; размерность величины дисперсии
 .
.
Оптические волокна со смещенной точкой нулевой дисперсии сегодня широко распространены. При выборе специальной формы функции показателя преломления световода можно сформировать требуемую спектральную дисперсионную зависимость световода с малым значением величины дисперсии в широкой области спектра. Примеры спектральной зависимости дисперсии одномодовых световодов с профилями показателей преломления
W- и ТС- типов показаны на рис. 32. 
Рис. 32. Спектральная зависимость дисперсии в одномодовых световодах
с
W-профилем показателя преломления (двухслойного) и трехслойного (ТС)-типа.При описании свойств одномодовых световодов нередко используется понятие дисперсионной длины
![]() , (114)
, (114)
где
![]() , (115)
, (115)
 , (116)
, (116)
 . (117)
. (117)
Величина коэффициента
 , (118)
, (118)
где
![]() . (119)
. (119)
Можно показать, что в одномодовом световоде выполняется следующая зависимость длительности
 (120)
(120)
и только при
Профильная дисперсия
В градиентных световодах как внутримодовая, так и межмодовая дисперсии зависят от параметра
![]() . (121)
. (121)
Подстановкой 85, 86 в 121, получим
 , (122)
, (122)
где групповой показатель преломления
![]() (123)
(123)
и параметр
 . (124)
. (124)
В теории градиентных световодов показано, что внутримодовая и межмодовая дисперсии волновода минимальны, если параметр профиля принимает оптимальное значение
![]() . (125)
. (125)
Типичное значение оптимального параметра профиля

Рис. 33. Спектральная зависимость оптимального параметра профиля градиентных световодов с различным составом материала сердцевины
Создание многомодовых градиентных световодов с дисперсией порядка нескольких десятков
Поляризационная дисперсия
Постоянные распространения ![]() ортогонально-поляризованных вдоль поперечных осей координат
ортогонально-поляризованных вдоль поперечных осей координат ![]() мод волоконного световода практически всегда различаются, при этом вводимое в световод излучение, как правило, одновременно возбуждает обе эти поляризованные моды. Вследствие неравенства
мод волоконного световода практически всегда различаются, при этом вводимое в световод излучение, как правило, одновременно возбуждает обе эти поляризованные моды. Вследствие неравенства ![]() и, соответственно, различия групповых задержек ортогонально-поляризованных мод, возникает дополнительное уширение регистрируемого импульса предаваемого излучения, которое можно охарактеризовать как межмодовую поляризационную дисперсию. Поляризационная дисперсия фактически возникает вследствие мелкомасштабных неоднородностей показателя преломления среды волновода, для описания которых используются различные статистические модели. В гауссовском приближении, уширение импульса вследствие поляризационной дисперсии прямо пропорционально
и, соответственно, различия групповых задержек ортогонально-поляризованных мод, возникает дополнительное уширение регистрируемого импульса предаваемого излучения, которое можно охарактеризовать как межмодовую поляризационную дисперсию. Поляризационная дисперсия фактически возникает вследствие мелкомасштабных неоднородностей показателя преломления среды волновода, для описания которых используются различные статистические модели. В гауссовском приближении, уширение импульса вследствие поляризационной дисперсии прямо пропорционально ![]() , где
, где ![]() - длина волновода, поэтому размерность поляризационной дисперсии обычно равна
- длина волновода, поэтому размерность поляризационной дисперсии обычно равна ![]() . Величина поляризационной дисперсии может быть соизмерима с величиной внутримодовой дисперсии одномодового световода и ее необходимо принимать во внимание при создании высокоскоростных, со скоростью передачи информации свыше 1 Гбит/с, протяженных систем связи.
. Величина поляризационной дисперсии может быть соизмерима с величиной внутримодовой дисперсии одномодового световода и ее необходимо принимать во внимание при создании высокоскоростных, со скоростью передачи информации свыше 1 Гбит/с, протяженных систем связи.
Ширина полосы пропускания световода
Разработчики оптических систем связи нередко используют понятие удельной ширины полосы пропускания (“пропускной способности”, “широкополосности”)
![]() ; (126)
; (126)
размерность
![]() , (127)
, (127)
где

Рис. 34. Зависимость ширины полосы пропускания световода от параметра профиля градиентного световода (а) и от длины волны (б)
В многомодовых световодах всегда имеет место взаимодействие мод, сопровождающееся перераспределением (“перекачкой”) энергии излучения между направляемыми модами и обусловленное дефектами волновода (неоднородностями, микротрещинами и др.), изгибами и наличием соединений оптоволокна. Параметр широкополосности, строго говоря, изменяется, при этом в результате усреднения групповых задержек межмодовая дисперсия ВС уменьшается, а зависимость уширения
![]() , (128)
, (128)
где
5.4.6. Поляризация излучения в волоконных световодах
Векторные характеристики (поляризацию) оптического излучения необходимо учитывать при построении систем когерентной оптической связи, нелинейно-оптических систем и при создании различных измерительных волоконно-оптических устройств, основанных на явлении интерференции света (волоконных интерферометров); напомним, что интерферируют (образуют интерференционную картину) когерентные волны одинаковой линейной поляризации.
Картины распределения силовых линий электрического вектора электромагнитного поля в поперечном сечении волоконного световода для различных типов колебаний (мод световода) могут значительно различаться - см. рис. 24. Эти картины особенно сложны для мод высших порядков и такие волноводные моды, вообще говоря, не являются поперечными. В слабонаправляющих

Рис. 35. Структура линейно-поляризованных мод
![]()

Рис. 36. Распределение вектора электрического поля в
Здесь ориентация вектора электрического поля в поперечном сечении волновода одинакова, а колебания поля в разных областях сечения сдвинуты по фазе на
С практической точки зрения, наибольший интерес представляет мода низшего порядка

Рис. 37. Ортогонально-поляризованные моды одномодового волоконного световода
В идеальном - бездефектном и прямом - световоде постоянные распространения ортогональных низших мод световода тождественно равны (
Сохранение линейной поляризации распространяющейся моды световода достигается искусственным увеличением разности
![]() . (129)
. (129)
При значительном различии
5.5. Оптические волокна, сохраняющие поляризацию излучения
Одномодовые оптические волокна, сохраняющие поляризацию излучения (
PM-fiber), должны иметь сильно различающиеся постоянные распространения ортогонально-поляризованных модЕсли сердцевина одномодового оптоволокна – эллипс с размерами большой и малой полуосей
 . (130)
. (130)
Одномодовые световоды с эллиптической сердцевиной поддерживают устойчивое состояние поляризации одной из возбужденных линейно-поляризованных мод. На практике световоды с некруглой сердцевиной используются сравнительно редко. Более технологичны и широко распространены сохраняющие поляризацию волоконные световоды с круглой сердцевиной. В таких световодах в плоскости, перпендикулярной оптической оси

Рис. 38. Поперечное сечение сердцевины волоконных световодов с сохранением поляризации. а – с эллиптической сердцевиной,
b – с круглой сердцевиной и анизотропией механических напряжений (Анизотропия показателя преломления в поперечном сечении волновода достигается вследствие эффекта фотоупругости и различия величин механических напряжений
![]() , (131)
, (131)
![]() , (132)
, (132)
где
Разность
![]() . (133)
. (133)
Величину двулучепреломления в одномодовых световодах характеризует длина биений
 . (134)
. (134)
Длина биений равна расстоянию, при котором произвольно поляризованная световая волна, распространяющаяся в световоде, восстанавливает свои исходные тип и форму поляризации. Типичные значения
Двулучепреломление в обычном одномодовом световоде возникает и при изгибах оптоволокна, сопровождающихся механическими напряжениями в волноводе, различными по величине в двух направлениях (
 , (135)
, (135)
где
 . (136)
. (136)
В волоконные световоды, сохраняющие поляризацию излучения, линейно-поляризованный свет должен вводиться с ориентацией электрического вектора поляризации излучения строго вдоль одной из осей (
![]() , (137)
, (137)
 . (138)
. (138)
Решая эту систему уравнений, находим, что относительная доля
 , (139)
, (139)
где скобки
 . (140)
. (140)
Относительная доля мощности излучения, переходящего в ортогональную моду, приблизительно равна
 , (141)
, (141)
где
5.6. Современное промышленное оптическое волокно
Промышленные разработки волоконных световодов (ВС) определяются областями их практического применения, среди которых важнейшие
Общепринята следующая классификация основных типов ВС:
- многомодовое оптическое волокно (МОВ)
5.6.1.Многомодовые ВС
Рабочие длины волн, как правило, в диапазоне около 0.85 и 1.30 мкм.
Типичные характеристики многомодовых ВС производства фирмы “
Corning” (США):
Таблица 4.
Параметры МОВ марки
InfiniCor|
Параметры |
МОВ-300 и МОВ-1000 |
МОВ-600 и МОВ-2000 |
|
Диаметр сердцевины, мкм |
62,5 |
50 |
|
Диаметр оболочки, мкм |
125 |
125 |
|
Диаметр покрытия, мкм |
245 |
245 |
|
Некруглость сердцевины, % |
5 |
5 |
|
Коэффицент потерь, дБ/км на длине волны 850 нм – на длине волны 1300 нм - |
менее 3 менее 0.7 |
менее 2.5 менее 0.8 |
|
Числовая апертура |
0.275 |
0.200 |
|
Длина волны нулевой дисперсии, нм |
1332….1354 |
1297….1316 |
|
Относительная разность показателей преломления, % |
2 |
1 |
|
Эффективный групповой показатель преломления в диапазоне 850 нм – в диапазоне 1300 нм - |
1496 1487 |
1490 1486 |
|
Типичная дальность передачи, м |
300, 1000 |
600, 2000 |
|
Стандартная длина на катушке, км |
2.2 – 2.8 |
1.1 – 4.4 |
|
Рабочая температура, Ц |
- 60 ….80 |
- 60….80 |
5.6.2. Одномодовые ВС
Диапазон рабочих длин волн, как правило, 1.30 и 1.55 мкм.
Типичные характеристики ООВ производства фирмы “
Corning” (США):Таблица 5.
Параметры ООВ “
Corning” – стандартного, типа SMF-28, и с большой эффективной площадью, типа LEAF|
Параметры |
SMF-28 |
LEAF |
|
Коэффициент потерь, дБ/км на длине волны 1310 нм - 1550 нм - 1625 нм |
0.34 0.20 - |
- 0.22 0.25 |
|
Диаметр поля моды, мкм на длине волны 1310 нм – 1550 нм - |
9.20 10.35 |
- 9.2… 10.0 |
|
Длина волны нулевой дисперсии, нм |
1301…..1321 |
- |
|
Хроматическая дисперсия, пс/нм.км На длинах волн 1530…1565 1565…1625 |
- - |
2.0….6.0 4.5….11.2 |
|
Поляризационная модовая дисперсия, пс/(км)1/2 |
0.2 |
0.2 |
|
Разность показателей преломления, % |
0.36 |
- |
|
Числовая апертура |
0.13 |
- |
|
Длина волны отсечки, нм |
1260 |
1260 |
Пример характеристик ООВ другой известной фирмы-производителя “
Alcatel”:Таблица 6.
Оптические параметры ООВ “
Alcatel” стандартного типа ASMF-200 и с большой эффективной площадью Teralight|
Параметры |
ASMF-200 |
Teralight |
|
Коэффициент потерь, дБ/км на длине волны 1310 нм – 1550 нм - |
0.34 0.25 |
- 0.28 |
|
Диаметр поля моды, мкм на длине волны 1310 нм – 1550 нм - |
9.1 - |
- 9.2 |
|
Хроматическая дисперсия, пс/нм.км на длине волны 1310 нм – 1550 нм - |
3.5 18 |
- 8 |
|
Длина волны нулевой дисперсии, нм |
1300…..1320 |
1440 |
|
Длина волны отсечки, нм |
1150…1330 |
1300 |
|
Эффективная площадь сечения, мкм 2 |
- |
65 |
|
Поляризационная модовая дисперсия, пс/(км)1/2 (на длине волны 1550 нм) |
0.1 |
0.1 |
Геометрические и механические параметры одномодовых волокон:
Таблица 7.
Параметры ООВ типа LEAF и Ttralight
|
Параметры |
LEAF |
Teralight |
|
Диаметр оболочки, мкм |
125 |
125 |
|
Эксцентриситет, мкм |
0.5 |
0.6 |
|
Некруглость оболочки, % |
1 |
2 |
|
Диаметр покрытия, мкм |
245 |
245 |
|
Радиус собственного изгиба волокна, м |
4 |
4 |
|
Прирост затухания, дБ/км на длине волны 1550 нм 1 виток, диаметр 32 мм, - 100 витков, диаметр 75 мм - |
0.50 0.05 |
0.50 0.05 |
|
Усилие снятия покрытия, Н |
3 |
1 |
Примечание
: прирост затухания при изгибе многомодового волокна существенно выше.5.6.3. Оптические волокна с сохранением поляризации
(PM)Двулучепреломляющие ВС обычно используются в волоконных гироскопах и в различных оптических датчиках физических полей (акустического, полей упругости, электромагнитных и др.). Наиболее распространены РМ-волокна с эллиптической напрягающей промежуточной оболочкой и волокно типа “
PANDA”.Таблица 8.
Оптические параметры РМ-волокна “
PANDA” производства фирмы “Corning”|
Диаметр оболочки и тип волокна |
Рабочая длина волны, нм |
Диаметр поля моды |
Длина биений, мм |
Развязка, дБ на 100 метров |
Потери, дБ/км |
|
250 мкм, РМ-850 РМ-1300 РМ-1550 |
850 1300 1550 |
5.5 9.5 10.5 |
3.0 4.0 5.0 |
25 25 25 |
3.0 1.0 0.5 |
|
400 мкм, РМ-980 РМ-1300 РМ-1550 |
980 1300 1550 |
6.6 9.5 10.5 |
3.3 4.0 5.0 |
25 25 25 |
3.0 1.0 0.5 |
Зарубежными и отечественными производителями выпускаются специализированные волоконные световоды, в том числе
Современные оптические технологии обеспечивают изготовление оптоволокна практически любой конфигурации и с высокими техническими характеристиками.
6. Оптоэлектронные компоненты волоконно-оптических систем передачи информации
В настоящем разделе приведены краткие сведения об основных оптоэлектронных устройствах, применяемых при построении ВОСПИ. Их номенклатура весьма разнообразна, а технические характеристики и функциональные возможности совершенствуются с каждым годом.
6.1. Полупроводниковые излучатели
В оптических системах связи и обработки информации могут применяться различные источники света (например, газовые и твердотельные лазеры, газоразрядные источники и др.). В ВОСПИ наиболее эффективно использование компактных и экономичных полупроводниковых излучателей. К ним относятся полупроводниковые лазеры, светодиоды и суперлюминесцентные диоды.
6.1.1. Полупроводниковые лазеры
Принцип действия полупроводниковых лазеров (ППЛ) основан на вынужденной излучательной рекомбинации электронно-дырочных пар, в активных полупроводниковых структурах, получаемых при прохождении через такие структуры электрического тока накачки. Наибольшее распространение получили лазеры на гетероструктурах (гетеролазеры), лазеры с распределенной обратной связью (РОС-лазеры) и лазеры на квантоворазмерных структурах (КРС-лазеры).
Современные ППЛ, применяемые в системах оптической связи, обычно работают в спектральных диапазонах высокой прозрачности кварцевого оптоволокна - 0.82-0.90 мкм, 1.30 – 1.33 мкм и около 1.55 мкм. Типичная мощность излучения таких ППЛ от 1 до 5 мВт; увеличение выходной мощности ППЛ для магистральных ВОСПИ
сверх 5-10 мВт нецелесообразно, так как срок действия мощных лазеров сравнительно невелик. Кроме этого, при больших плотностях мощности в одномодовом волокне заметную роль начинают играть нелинейно-оптические явления – ВКР, ВРМБ и др., приводящие к искажениям передаваемых сигналов. Ширина спектра излучения лучших образцов промышленных полупроводниковых лазеров около 0.1 нм при уровне боковых частот ниже 20 дБ. В одночастотных ППЛ, используемых в системах когерентной оптической связи, полуширина спектра генерации менее 500 МГц. Величина порогового тока накачки РОС-лазеров составляет несколько десятков мА, у ППЛ на основе квантоворазмерных структур пороговый ток накачки существенно меньше – от 3 до 15 мА.Как правило, ППЛ для ВОЛС выпускаются в виде компактных оптоэлектронных модулей, содержащих сервисную электронику (усилитель подводимого сигнала, систему авторегулировки мощности, температуры и др.), фотоприемник для контроля мощности выходного излучения, терморезистор и полупроводниковый термоэлемент (элемент Пельтье) - “холодильник”, управляемый специальным электронным устройством и поддерживающий стабильную рабочую температуру внутри модуля. В таком модуле излучение из активной области ППЛ с использованием микролинз вводится в выходное одномодовое или многомодовое оптоволокно.
В последние годы выпуск отдельных излучательных полупроводниковых модулей для ВОСПИ становится ограниченным, и гораздо большее распространение в технике оптической связи находят приемо-передающие оптоэлектронные модули, содержащие в едином компактном блоке полупроводниковые излучатель и фотоприемник.
Частота модуляции современных коммерческих высокоскоростных ППЛ составляет от нескольких десятков – сотен МГц до примерно 1.5 – 2.5 ГГц. В уникальных образцах ППЛ достигнута скорость передачи сигналов свыше 25 Гбит/с.
В последние годы повышенный интерес разработчиков ВОСПИ вызывают “викселы” - полупроводниковые лазеры с вертикальным резонатором (
VCSEL – vertical-cavity surface-emitting lasers). В таких лазерах резонатор образован двумя объемными дифракционными решетками Брэгга и излучение генерируется в направлении, перпендикулярном плоскости подложки, являющейся основанием гетеро- и квантоворазмерных слоев полупроводников. Благодаря сверх-короткой длине6.1.2. Полупроводниковые светодиоды
В ВОСП небольшой (0.1-1.0 км) протяженности, а также в низкоскоростных (не боле 10 Мбит/с) ВОСП в качестве источников света нередко используются полупроводниковые светодиоды, отличающиеся сравнительно малой мощностью излучения (до 0.5 мвт) и большой (около 20-30 нм) шириной спектра излучения. В основе действия светоизлучающих полупроводниковых диодов (СИД) лежит спонтанная рекомбинация электронно-дырочных пар в активной области гетеро- либо квантоворазмерной полупроводниковой структуры. Диапазон рабочих длин волн современных СИД весьма широк – от 0.4 до
1.6 мкм. СИД активно используются и в технике систем индикации, в осветительной и сигнальной технике; разработаны СИД с мощностью излучения до 30 мВт в диапазонах длин волн около 690, 590, 470 нм, а также различные типы СИД белого свечения. Степень поляризации выходного излучения СИД близка к нулю. СИД обычно используются в линиях передачи сигналов на основе многомодовых волоконных световодов с большим (десятки-сотни мкм) диаметром сердцевины, в том числе изготовленных из недорогих полимерных материалов. Удобно применение СИД и в открытых системах связи с дальностью действия в пределах 100 м, используемых на промышленных объектах и строительных площадках. Характерная особенность СИД, применяемых в системах связи, – линейная ватт-амперная характеристика в широком диапазоне токов накачки, что делает их весьма удобными в аналоговых оптоэлектронных системах передачи и обработки сигналов. Основные достоинства СИД – малая потребляемая электрическая мощность, дешевизна и значительная долговечность (около6.1.3. Суперлюминесцентные диоды
В суперлюминесцентных диодах (СЛД) последовательно действуют два процесса генерации света: первичное излучение возникает в результате спонтанной рекомбинации электронно-дырочных пар и вторичное - вынужденное излучение – является основой механизма усиления спонтанного излучения в активной среде. Активная среда в СЛД обладает высоким оптическим коэффициентом усиления, оптический резонатор в СЛД отсутствует и такой излучатель, в целом, можно рассматривать как однопроходный усилитель света. В конструкции СЛД достигнута высокая степень подавления лазерных (резонансных) эффектов, в результате чего широкая, с полушириной около 20-40 нм, спектральная кривая распределения мощности выходного излучения примерно соответствует распределению Гаусса. Мощность излучения СЛД обычно находится в пределах 3 - 10 мВт (имеются промышленные образцы СЛД мощностью в несколько сотен мВт) при токах накачки величиной от 50 до 150 мА. Спектральный риппл (относительная величина резонансных максимумов на спектральной зависимости мощности излучения) в лучших образцах СЛД менее 0.5 %. Излучение СЛД частично поляризовано (степень поляризации 30-40%), а ватт-амперная характеристика таких излучателей существенно нелинейна. В ВОСПИ СЛД применяются сравнительно редко и основной областью их практического использования являются различные оптические измерительные устройства (например, волоконные гироскопы), датчики, системы индикации.
6.2. Фотоприемники
В ВОСПИ обычно используются полупроводниковые фотоприемники (
p-I-n – и лавинные фотодиоды), в специальных приложениях возможно применение и других приемников оптического излучения – фоторезисторов, фототранзисторов, болометров, фотоумножителей и др.6.2.1. p-I-n
-фотодиодыp-i-n
- фотодиод представляет собой трехслойную структуру из p- и n- полупроводников, разделенную сравнительно протяженной I – областью слаболегированного полупроводника. Поглощение квантов света происходит в обедненной I- области, при этом в результате внутреннего фотоэффекта в объеме этого слоя образуются электроны и дырки, время жизни которых намного превышает их время жизни в p- и n- слоях (где они быстро рекомбинируют). Во внешнем электрическом поле носители заряда дрейфуют, обусловливая электрический ток в замкнутой электрической цепи фотоприемного устройства. Спектральная чувствительность p-I-n фотодиодов определяется типом полупроводниковой структуры, при этом красная граница фотоэффекта составляет около 0.9 мкм для арсенида галлия, 1.1 мкм для кремния и 1.7 мкм для германия; сегодня разработаны и практически используются более сложные фотоприемные полупроводниковые структуры, в том числе квантоворазмерные, обладающие высокой квантовой эффективностью как в узкой, так и в широкой полосах спектра длин волн. В лучших образцах p-I-n фотодиодов чувствительность фотодиода (отношение величины фототока к мощности падающего излучения) достигает уровня свыше 0.9 А/Вт. Временные характеристики p-I-n фотодиодов определяются толщиной обедненного I-слоя, скоростью дрейфа носителей заряда и собственной емкостью фотодиода и подводимых электродов. Высокоскоростные p-I-n фотодиоды характеризуются временем нарастания-спада регистрируемого оптического сигнала величиной 10 - 100 пикосекунд. Величина обратного напряжения смещения в p-I-n- фотодиодах обычно от 10 до 20 В.
6.2.2. Лавинные фотодиоды
Лавинные фотодиоды (ЛФД) относятся к полупроводниковым фотоприемникам с внутренним усилением фототока. Конструктивно в лавинных фотодиодах между областью поглощения света (
6.2.3. Отношение сигнал/шум и минимальная регистрируемая мощность фотоприемников
Фотоэффект по физической природе – типичный вероятностный, случайный процесс, строгое описание которого требует использования статистических методов. В основе современного описания фотоэффекта лежит положение, что мгновенная вероятность фотоэмиссии (вероятность образования электронно-дырочной пары при поглощении света в объеме полупроводника) прямо пропорциональна мгновенной классической интенсивности электромагнитного поля в рассматриваемой “точке” этого объема. Полупроводниковый фотоприемник, в целом, можно рассматривать как источник тока, включенный в замкнутую электрическую цепь, содержащую источник напряжения обратного смещения и резистор нагрузки. Важной характеристикой фотоприемного устройства является величина отношения сигнала (
 . (142)
. (142)
Отношение сигнал/шум равно
 , (143)
, (143)
где
![]() (144)
(144)
(![]()
При проектировании высокоскоростных оптических систем связи важной характеристикой фотоприемного устройства является минимальная (пороговая) регистрируемая мощность
 , (145)
, (145)
где
![]() ; (146)
; (146)
в этой формуле множитель

Рис. 39. Зависимость минимальной регистрируемой мощности
Мощность излучения на рис.39 обозначена в размерности дБм (децибелл относительно 1 мВт), определяемой как
Итак, согласно рис. 39, увеличение скорости передачи информации по оптическому каналу связи неизбежно сопровождается уменьшением чувствительности фотоприемного устройства. Поэтому в разработках ВОСПИ со сверхвысокими, например, свыше 10 Гбит/с, скоростями передачи сигналов особенно необходим компромисс при выборе скорости передачи информации и длины регенерационного участка линии передачи.
6.3. Оптические соединители и разветвители
Волоконно-оптические системы связи нередко содержат множество оптических соединений, обеспечивающих требуемую структуру (“топологию”) сетей связи.
Оптические неразъемные соединители сварного типа характеризуются рекордно малыми оптическими потерями, менее 0.1 дБ. Такие соединители применяются при монтаже как объектовых, так и протяженных (магистральных) линий связи. В последнем случае, на длине регенерационного участка, например, от 30 до 60 км требуется до 20-30
соединений (строительная длина оптического кабеля обычно составляет 2-3 км). Современная технологическая аппаратура сварки оптических волокон автоматизирована и позволяет эффективно, в полевых условиях, соединять оптоволокно с любыми характеристиками.Разъемные оптические соединители (коннекторы) обеспечивают высокоточное сближение торцов и координацию оптических осей соединяемых оптических волокон. Оптические потери в лучших образцах разъемных коннекторов составляют примерно 1-2 дБ, уровень обратного отражения около 30 дБ. Современная номенклатура промышленно выпускаемых коннекторов весьма разнообразна (одномодовые, многомодовые, многополюсные и др.). Некоторые типы коннекторов содержат шариковые либо градиентные микролинзы. Торцам соединяемых оптических волокон часто придается сферическая форма (для уменьшения обратного отражения света), существуют коннекторы и с плоскими торцами закрепленного в них оптоволокна, скошенными под небольшим углом, с целью уменьшения оптических потерь при прохождении линейно-поляризованных мод волновода.
Оптические разветвители представляют собой многополюсные устройства, вообще говоря, с несколькими входами и выходами, назначение которых – обеспечить требуемое распределение оптической мощности между подводимыми оптическими волноводами. Основными параметрами разветвителей являются оптические потери, переходное затухание между встречными направлениями передачи сигналов, уровень обратного рассеяния, уровень искажений поляризации и модового состава распространяющегося излучения. Оптические разветвители изготавливаются как с использованием технологий сварки оптоволокна, так и с применением различных микрооптических элементов (шариковых линз, призм, граданов и др.).
6.4. Оптические мультиплексоры и демультиплексоры
Оптические мультиплексоры и демультиплексоры (МДМ) применяются в оптических системах связи со спектральным уплотнением каналов (с одновременной передачей по оптоволокну сигналов с различными длинами волн –
WDM-systems) и их можно отнести к категории спектрально-селективных оптических разветвителей. Мультиплексоры выполняют функции объединения оптических несущих с разными длинами волн (обычно они имеют несколько входов и один выход), демультиплексоры – обратную процедуру разделения оптических несущих по длинам волн (один вход, несколько выходов). Основные характеристики МДМ – тип (одномодовый либо многомодовый), число рабочих спектральных каналов, оптические потери в каждом канале, величина переходного затухания, уровень обратного рассеяния, уровень вносимых поляризационных искажений. Диапазон рабочих длин волн и величина разноса спектральных несущих также являются важными параметрами МДМ. В наиболее освоенных сегодня WDM-системах число рабочих каналов обычно составляет 2, 4 или 6, разнос длин волн несущих – несколько единиц нм, оптические потери в каналах 0.5 – 2 дБ (отметим, что теоретически потери в спектрально-селективных разветвителях, в отличие от широкополосных, могут приближаться к нулю). В разрабатываемых “плотных” DWDM-системах спектрального уплотнения число рабочих каналов – несколько десятков (до 30 и более), разнос частот несущих несколько единиц-десятков ГГц, оптические потери в канале на уровне 1 дБ.Конструктивно мульти-демультиплексоры нередко выполнены на основе объемных микрооптических элементов (микролинз, граданов) и содержат спектрально-селективные устройства – отражательную вогнутую либо плоскую дифракционную решетку, интерференционный фильтр, объемную голограмму, дисперсионную призму и др. Волноводные МДМ, например, на основе интегрально-оптических волноводов, часто представляют собой аналоги классических интерферометров – Фабри-Перо, Маха-Цендера, эшелона Майкельсона и др. В последнее время внимание разработчиков МДМ привлекают волоконные решетки Брэгга (
FBG), являющиеся, в сущности, объемными отражательными голограммами, сформированными в сердцевине оптоволокна.6.5. Оптические коммутаторы
Оптические коммутаторы (переключатели) применяются в системах оптической связи для переключения сигналов в оптических сетях. Основные характеристики оптических коммутаторов (ОК) – емкость (число входов и выходов), быстродействие (скорость переключения), оптические потери в канале передачи сигнала (коэффициент ослабления в положении “включено”) и переходные помехи (переходное
затухание – коэффициент ослабления в положении “выключено”). В высококачественных ОК указанные оптические характеристики рассматриваются с учетом длины волны и поляризации излучения. Наиболее распространены сегодня оптические переключатели, управляемые электрическими сигналами. В перспективных системах оптической связи и в разрабатываемых оптических компьютерах предполагается использование оптически управляемых ОК.Оптические коммутаторы, в зависимости от принципа действия, подразделяются на восемь типов: механические ОК, электрооптические, термооптические, интегрально-оптические, полупроводниковые (
SOA), ОК на фотонных кристаллах и ОК на многослойных жидкокристаллических матрицах.Технические характеристики современных ОК значительно различаются. Например, механические коммутаторы имеют время переключения от 10 до 500 мс, вносимые потери около 0.5 дБ, переходное затухание до 80 дБ, число входных и выходных портов от 50 до 1600. Быстродействие электрооптических ОК существенно выше, 10-100 пс, но их емкость обычно мала, например, 1х2 и 2х2. При последовательном включении нескольких таких ОК емкость составного ОК, очевидно, возрастает. В последние годы внимание разработчиков оптических коммутаторов привлекают микромеханические коммутаторы (
MEMS-типа), в которых использованы технологии как микроэлектроники, так и интегральной оптики.6.6. Оптические изоляторы
Оптические изоляторы (ОИ) это устройства, имеющие большой коэффициент пропускания оптического излучения в прямом направлении и весьма малый – в обратном. Такие устройства обычно применяются в высокоскоростных ВОСПИ для устранения влияния на полупроводниковый излучатель света, рассеянного в оптической линии передачи сигналов, – на разъемных соединителях, участках сварки волокна, разветвителях и на неоднородностях материала непосредственно в волоконно-оптическом кабеле. Обратно-рассеянное излучение, действуя на активную среду полупроводникового излучателя, вызывает шумы и флуктуации мощности излучения ЛД. Оптические изоляторы используются в обычных и когерентных оптических системах связи, а также являются составной частью высокочувствительных оптических измерительных устройств, например, волоконных гироскопов.
Действие оптических изоляторов всегда основано на магнитооптическом эффекте Фарадея – вращении плоскости поляризации света в образце, помещенном в магнитное поле, силовые линии которого ориентированы вдоль светового луча. Характерно, что поворот плоскости поляризации (ПП) при эффекте Фарадея не зависит от направления распространения светового луча в образце и при многократном прохождении луча света в таком образце полный угол поворота ПП увеличивается. Конструктивно ОИ содержит два линейных поляризатора (входного и выходного) с осями пропускания, расположенными под углом 45 градусов, и магнитооптического кристалла с большим значением постоянной Верде, например железоиттриевого граната, помещенного в постоянное магнитное поле.
В лучших образцах ОИ оптические потери в прямом направлении равны около 1.0-1.5 дБ, величина развязки – до 30-40 дБ. Оптические изоляторы обычно действуют в сравнительно узкой (30-80 нм) полосе спектра рабочих длин волн и согласованы с входным и выходным световодами, изготовленными из оптоволокна с сохранением поляризации излучения.
6.
7. Внешние оптические модуляторыНаиболее распространенным способом амплитудной модуляции оптического сигнала в ВОСПИ является изменение тока накачки излучателя. При больших, свыше 1-2 ГГц, частотах модуляции тока накачки в полупроводниковых лазерах заметную роль начинает играть квазирезонансный эффект, сопровождающийся амплитудными шумами, значительным уширением спектра оптического сигнала и ограничением величины частоты модуляции. Поэтому при создании ВОСПИ с наивысшей, в десятки-сотни и более ГГб/с, пропускной способностью наиболее эффективным способом модуляции сигнала является применение в ВОСПИ внешних оптических модуляторов (ВОМ). В этом случае полупроводниковый лазер работает в непрерывном режиме, а внешний оптический модулятор установлен в оптическом тракте непосредственно за оптическим изолятором и источником света.
Действие наиболее распространенных внешних оптических модуляторов основано на электрооптическом (Поккельса), магнитооптическом (Фарадея), электроабсорбционном и акустооптическом (Брэгга или Рамана-Ната) эффектах. Такие ВОМ работоспособны практически во всех диапазонах оптической связи с частотами модуляции свыше 1 ГГц. Амплитудные ВОМ могут быть выполнены на основе интегрально-оптического интерферометра Маха-Цендера с фазовой модуляцией в одном из плеч интерферометра. Разрабатываются высокоскоростные ВОМ и на основе полупроводниковых многослойных структур, а также МОП-структур в виде тонких слоев металла и диэлектрика. Сегодня созданы экспериментальные ВОЛС протяженностью 160 км на основе ВОМ со скоростью передачи в одном канале 111 Гбит/с, что при использовании принципа спектрального уплотнения обеспечивает эквивалентную пропускную способность ВОСПИ порядка 10 Тбит/
c.6.8. Оптические усилители
Оптический усилитель (ОУ) увеличивает мощность оптических сигналов в ВОСПИ без их промежуточного преобразования в электронные сигналы. Такой способ усиления особенно удобен в ВОСПИ со спектральным уплотнением, благодаря возможности одновременного усиления нескольких информационных сигналов с различными длинами волн. Наиболее распространены два типа оптических усилителей – полупроводниковый квантовый усилитель (ПКУ) и волоконно-оптический (например, эрбиевый) усилитель.
В полупроводниковом квантовом усилителе усиливающей свет средой является тонкий “активный” волноводный слой на границе полупроводников
p- и n- типов, через который проходит электрический ток накачки. Конструкция ПКУ подобна конструкции обычного полупроводникового лазера, коэффициент отражения зеркал резонатора у которого близок к нулю. Усиливаемое излучение обычно вводится в активный волновод ПКУ при его прямом согласовании (стыковке) с подводимым оптическим волокном; похожим образом усиленное излучение выводится из активного волновода.В волоконно-оптическом усилителе также используется лазерный принцип усиления, при этом свет проходит через оптическую инверсную среду, в которой населенность верхних электронных состояний выше, чем нижних, что обеспечивается благодаря оптической накачке
.Коэффициент усиления
 ; (147)
; (147)
часто коэффициент усиления ОУ исчисляется в дБ, при этом
![]() , (148)
, (148)
где
Средняя длина волны и ширина полосы частот усиления ПКУ зависит от типа “твердого раствора” активной полупроводниковой среды и ширины соответствующей запрещенной зоны. В ближнем ИК-диапазоне длин волн около 1.3 и 1.55 мкм типичная ширина полосы усиления ПКУ примерно равна 30-40 нм. В ПКУ используются те же принципы создания активных сред, что и в полупроводниковых лазерах, в том числе, здесь возможно применение полупроводниковых гетероструктур и квантоворазмерных структур. Сегодня созданы ПКУ с коэффициентом усиления до 30 дБ.
В волоконно-оптических усилителях спектральные характеристики ОУ полностью определяются структурой энергетических уровней рабочего материала (ионов неодима, эрбия, германия и др.). В однородно уширенной среде волоконно-оптического усилителя с оптической накачкой, вследствие явления насыщения усиления, величина коэффициента усиления
 , (149)
, (149)
где

Рис. 40. Зависимость коэффициента усиления оптического усилителя от мощности входного (усиливаемого) сигнала
Принципиальная схема волоконно-оптического усилителя на основе кварцевого оптоволокна, легированного ионами эрбия, показана на рис. 41.

Рис. 41. Принципиальная схема волоконно-оптического усилителя. 1 – источник накачки (мощный полупроводниковый лазер с длиной волны излучения 980 нм или 1480 нм), 2 – мультиплексор, 3 – эрбиевое оптоволокно, 4 – полосовой оптический фильтр с пропусканием на длине волны усиливаемого сигнала 1550 нм.
Структура энергетических уровней трехвалентного иона эрбия в кварцевом стекле, и схема поглощения излучения накачки, безызлучательного и рабочего переходов в полосе длин волн 1520-1570 нм показаны на рис. 42.

Рис. 42. Энергетические уровни иона эрбия; инверсия населенности создается между неоднородно уширенными уровнями
Шумовые характеристики оптических усилителей описываются посредством
NF-фактора (Noise Figure), равного отношению отношений сигнал/шум на входе и на выходе усилителя,  , (150)
, (150)
которое также часто оценивается в дБ -
 , (151)
, (151)
где
Эрбиевые волоконно-оптические усилители вызывают особенный интерес у разработчиков магистральных ВОСПИ, так как длины волн усиления в таких ОУ хорошо совпадают с областью минимальных потерь кварцевого оптоволокна, близкой к 1550 нм. Кроме этого, именно эрбиевые усилители обладают высокими параметрами при сравнительно небольших мощностях излучения накачки и длинах активного оптоволокна. Типичные рабочие характеристики волоконно-оптических эрбиевых усилителей приведены на рис. 43.

Рис. 43. а. - зависимость коэффициента усиления
Полезным свойством волоконно-оптических усилителей является возможность реализации в них двунаправленной оптической накачки, то есть одновременного ввода излучения накачки (например, для эрбиевого усилителя - на длинах волн 980 нм или 1480 нм) с разных концов отрезка активного оптоволокна. В таком случае спектральные мультиплексоры, посредством которых в усиливающее оптоволокно вводится излучение накачки, расположены с обеих сторон этого волокна. В лучших образцах волоконно-оптических эрбиевых усилителей, на длине волны 1550 нм, достигнуто усиление величиной до 45 дБ и
7. Энергетический потенциал оптической линии связи
Энергетический потенциал (ЭП, “link loss budget”) оптической линии связи, выражаемый в дБ, равен десяти логарифмам отношения мощности
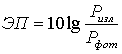 . (152)
. (152)
Если мощность источника и чувствительность фотоприемника выразить в дБм (в децибеллах относительно уровня 1 мВт), очевидно,
![]() . (153)
. (153)
Энергетический потенциал удобен при расчетах допустимых потерь в элементах, составляющих линию связи. Например, для ВОСПИ, показанной на рис. 44, баланс (“расход”) ЭП выражается уравнением
![]() , (154)
, (154)
где
(дБ/км),

Рис. 44. Пример оптической линии связи. 1 – излучатель, 2 – разъемные соединители, 3 – волоконно-оптический кабель, 4 – неразъемные соединители, 5 – фотоприемник.
Введение “энергетического запаса” необходимо на практике для учета различных дестабилизирующих факторов – старения оптоволокна, изменений рабочей температуры компонент ВОСПИ, флуктуаций мощности источников питания и др.
Типичные значения ЭП составляют от 50 до 70 дБ и существенно зависят от скорости передачи информации.
Основными методами увеличения пропускной способности (скорости передачи информации) в ВОСПИ являются
Помимо названных способов, в стадии лабораторного исследования находятся поляризационное уплотнение и уплотнение, основанное на использовании когерентных свойств оптического излучения.
Временное уплотнение (TDM) состоит в увеличении частоты передачи сигналов, то есть в использовании при передаче (в цифровом режиме кодирования) импульсных сигналов минимальной длительности и скважности. В режиме модуляции тока накачки полупроводниковых излучателей достигнута наивысшая скорость передачи информации около 30 Гбит/с. При использовании внешних волноводных модуляторов максимальная частота модуляции оптических сигналов достигает нескольких сотен Гбит/с.
Пространственное уплотнение состоит в увеличении числа оптических волокон в многожильном волоконно-оптическом кабеле. Разработаны многожильные оптические кабели связи с числом волокон 2, 4,…12, 24,…. 144 и т. д. как ленточного так и радиально-симметричного типов. Увеличение числа волокон в кабелях связи способствует многократному увеличению пропускной способности ВОСПИ, но, конечно, осложняет проблему соединения таких кабелей.
Спектральное уплотнение (WDM) (уплотнение по длинам волн) состоит в одновременной передаче по одножильному оптическому кабелю нескольких оптических сигналов с различными длинами волн несущих. В пределах спектральной полосы прозрачности кварцевого волокна можно разместить несколько информационных сигналов и тем самым многократно увеличить пропускную способность одножильного ВОК (рис. 45).

Рис. 45. Принцип спектрального уплотнения
В обычных
WDM-системах расстояние 
Рис. 46. Принципиальная схема ВОСПИ со спектральным уплотнением каналов.
MUX –мультиплексор, DEMUX –демультиплексор.В сравнительно коротких, без использования оптических усилителей, ВОСПИ принцип спектрального уплотнения позволяет реализовать дуплексный режим передачи сигналов без временного разделения сигналов, передаваемых во встречном направлении (на длине волны
Мультиплексоры-демультиплексоры для ВОСПИ со спектральным уплотнением должны обладать минимальными оптическими потерями в рабочих каналах и минимальным уровнем переходных помех. В таких устройствах в качестве спектрально-селективных устройств применяются диспергирующие призмы, фокусирующие отражательные дифракционные решетки, интерференционные фильтры, объемные голографические элементы, волноводные решетки Брэгга и др. Оптические потери
 , (155)
, (155)
где
Спектральное уплотнение, особенно в режиме
DWDM, допускает передачу по одномодовому ВОК в каждом из спектральных рабочих каналов информационных сигналов с очень большой частотой (до десятков-сотен Гбит/с) и считается сегодня одним из перспективных направлений развития магистральных ВОСПИ.Идея модового (углового) уплотнения (МУ) состоит в передаче оптических сигналов по многомодовому оптическому волокну на разных оптических модах волновода. Принцип модового уплотнения поясняется на рис. 47.

Рис. 47. Модовое (угловое) уплотнение каналов. Угол при вершине конуса на выходе многомодового ВС равен углу ввода излучения при возбуждении соответствующих 1, 2, 3,… групп мод.
Здесь используется свойство многомодового волокна сохранять угловую ориентацию раздельно возбужденной группы мод. Число
![]() , (156)
, (156)
где
9. Когерентные оптические системы связи
Любой фотоприемник регистрирует лишь усредненную по времени мощность принимаемого оптического сигнала, при этом информация о фазе и частоте падающей на фотоприемник световой волны утрачивается (впрочем, флуктуации фототока характеризуют когерентные свойства поглощенного излучения – эффект Брауна-Твисса). Перенос в фототок информации о фазе и частоте падающего на фотоприемник света возможен при когерентном фотодетектировании излучения, принцип которого аналогичен гетеродинному детектированию сигналов, широко используемому в радиотехнике.
При некогерентном фотодетектировании сигнал с выхода фотоприемника усиливается электронным полосовым усилителем низких (по отношению к оптическим) частот с шириной полосы

Рис. 48. Некогерентное (прямое) (а) и когерентное (гетеродинное либо гомодинное) (б) детектирование света
Отношение сигнал/шум на выходе усилителя при прямом фотодетектировании представляется формулой
 , (157)
, (157)
где
При когерентном, рис. 48-б, фотодетектировании на фотоприемник вместе с регистрируемым оптическим сигналом с частотой
![]() , (158)
, (158)
и
![]() , (159)
, (159)
то зависящий от времени фототок
![]() . (160)
. (160)
Подстановкой 158 и 159 в 160, и выполнив усреднение по времени (фотоприемник не реагирует на переменные сигналы с оптическими частотами), находим
![]() . (161)
. (161)
Выражение 161 описывает переменный сигнал биений фототока на “промежуточной” (в терминах радиотехники) частоте
который прямо зависит от амплитуд и фаз направляемых на фотодетектор сигналов. При
Если мощность сигнала гетеродина намного больше мощности принимаемого оптического сигнала, то есть
 . (162)
. (162)
Ввиду малой, по сравнению с оптической частотой, величины промежуточной частоты
Когерентное фотодетектирование целесообразно использовать при приеме маломощных оптических сигналов; например, для промежуточной частоты величиной
Амплитуда сигнала биений существенно зависит от пространственных условий гетеродинирования – угла

Рис. 49. Пространственные условия оптического гетеродинирования
При
 , (163)
, (163)
где
Достоинствами когерентных оптических систем связи является высокая чувствительность при приеме слабых оптических сигналов и возможность реализации частотной и фазовой модуляций сигнала. Их недостатком является сравнительно высокие сложность и стоимость - в таких системах необходимо использовать высокостабильные узкополосные излучатели (с шириной спектра, например, около 1 МГц) и устройства коррекции поляризационных характеристик оптических сигналов. Пример схемы ВОСП с когерентным фотодетектированием приведен на рис. 50.

Рис. 50. Схема ВОСП с когерентным детектированием сигналов. 1. – узкополосный (одночастотный) лазер, 2 – оптический изолятор, 3 – модулятор (АМ, ЧМ либо ФМ) сигнала, 4 - одномодовое оптоволокно (оптическая линия передачи), 5 – мультиплексор (смеситель), 6 – поляризационный контроллер, 7 – перестраиваемый по частоте гетеродин (лазер), 8 – фотодетектор, 9 – демодулятор сигнала, 10 – устройство автоматической подстройки частоты (АПЧ), 11 – усилитель низкой (промежуточной) частоты.
Когерентное фотодетектирование может применяться не только в ВОСПИ, но и в открытых системах связи. Например, использование мощного
10. Оптические солитоны в ВОСПИ
Возможность использования в волоконно-оптических линиях передачи сигналов сверхкоротких, длительностью порядка 1-10 пс, оптических импульсов – оптических солитонов - обсуждается уже свыше 30 лет. Нелинейный по своей природе, солитонный режим передачи оптических сигналов является одним из способов реализации принципа временного уплотнения (TDM) информации в ВОСПИ. Предполагается, что именно при солитонном режиме будут достигнуты предельные, порядка единиц Тбит/с, скорости передачи данных вблизи одной спектральной несущей по одномодовому оптоволокну.
Сущность нелинейной волоконной оптики состоит в том, что при достаточно больших плотностях мощности излучения в световоде свет прямо воздействует на среду распространения, в результате чего показатель преломления материала сердцевины ВС изменяется. Мгновенные изменения показателя преломления
![]() , (164)
, (164)
где
![]() , (165)
, (165)
где
 . (166)
. (166)
Дисперсионная длина
 , (167)
, (167)
где
Волновое уравнение для амплитуды световой волны, в пренебрежении оптическими потерями в волноводе, имеет вид
 , (168)
, (168)
где время
![]() , (169)
, (169)
вклад обоих слагаемых в 168 соизмерим по величине и нелинейность направляющей среды существенно влияет на спектральные и временные характеристики распространяющегося импульсного сигнала.
Особенный интерес вызывает случай отрицательных значений
1.27 мкм, рис. 51.

Рис. 51. Спектральная зависимость показателя преломления (а) и дисперсии (б) кварцевого стекла. Длина волны нулевой дисперсии равна 1.27 мкм.
В этой области возможны решения уравнения 168 вида
 , (170)
, (170)
где
Выражение 170 описывает фундаментальный оптический солитон – импульсный оптический сигнал, форма огибающей которого не зависит от проходимого расстояния

Рис. 52. Временная зависимость мгновенной мощности
P=Солитонный режим распространения импульсного сигнала “физически” поясняется так. В среде с отрицательной (

Рис. 53. Изменение мгновенной частоты
Вследствие влияния оптической нелинейности, возникает дополнительная фазовая самомодуляция (ФСМ) сигнала, при этом мгновенная частота сигнала на переднем фронте оптического импульса, наоборот, уменьшается, а на заднем – увеличивается относительно средней частоты
Необходимым условием образования фундаментального солитона (“уединенной волны”) является равенство
 . (171)
. (171)
Например, для обычного кварцевого одномодового волокна на длине волны 1.55 мкм при
Приводимые оценки справедливы для оптического волокна без потерь и с учетом ослабления излучения условия образования оптических солитонов заметно усложняются. Согласно практическим оценкам, оптические солитоны могут возбуждаться в оптоволокне с потерями не более 0.2 дБ/км и при построении протяженных линий передачи таких сигналов для компенсации потерь мощности излучения необходимо использовать оптические усилители. С другой стороны, солитонный режим распространения сигналов требует весьма точного согласования эффектов ДГС и ФСМ, он чувствителен к влиянию различных дефектов оптоволокна, наличию соединений, разветвителей, влиянию других нелинейных явлений (ВКР, ВРМБ и др.).
В лабораторных условиях была продемонстрирована возможность передачи оптических сигналов в солитонном режиме по одномодовому оптоволокну (с включенными в линию передачи оптическими усилителями и переключателями) на расстояние в несколько тысяч км со скоростью свыше 30 Гбит/с.
Практическая целесообразность создания солитонных ВОСПИ должна быть оценена не только с учетом достижения рекордно высоких скоростей передачи данных, но и с учетом баланса энергетического потенциала линии связи. В частности, следует принимать во внимание уменьшение пороговой чувствительности
фотоприемных устройств по мере роста частоты передачи сигналов, а также надежность и стоимость оборудования связи.
Заключение
Оптические системы передачи информации являются одним из наиболее перспективных современных направлений в области техники связи, вобравшим в себя лучшие достижения микроэлектроники, волоконной оптики, интегральной оптоэлектроники, физики и техники полупроводников. Научные проблемы освоения оптического диапазона связи к настоящему времени, в значительной степени, решены и дальнейшее развитие оптических систем передачи информации существенно зависит от уровня и состояния технологии производства оптических и оптико-электронных компонент таких систем. Это не исключает возможности выдвижения и реализации новых идей в области физики и техники оптических систем передачи информации, основанных на весьма разнообразных свойствах как оптического излучения, так и применяемых в таких системах оптических материалов, их сложных композиций и структур.
Литература
Введение……………………………………………………………………...3
световодах…………………………………………………………….28
и бесконечным радиусом оболочки………………………………....31
преломления………………………………………………………..…37
передачи информации……………………………………………………62
фотоприемников………………………………………………………66
Заключение……………………………………………………………… ..91
Литература…………………………………………………………………92
В 2007 году СПбГУ ИТМО стал победителем конкурса инновационных образовательных программ вузов России на 2007–2008 годы. Реализация инновационной образовательной программы “Инновационная система подготовки специалистов нового поколения в области информационных и оптических технологий” позволит выйти на качественно новый уровень подготовки выпускников и удовлетворить возрастающий спрос на специалистов в информационной, оптической и других высокотехнологичных отраслях экономики.
Кафедра Твердотельной оптоэлектроники (ТТОЭ)
организована в 1988 году, в период активного развития оптоэлектроники как компонентной базы высокоскоростных систем передачи и обработки информации, и ее выделения в самостоятельную область науки, техники и производства.Специалисты кафедры обладают большим опытом научной, преподавательской и производственной деятельности, кафедра располагает оснащенными учебными и научными лабораториями.
Выпускники кафедры ТТОЭ получают специальную подготовку по прикладной и физической оптике, физике полупроводников, полупроводниковой оптической технике, оптическим методам передачи и обработки информации, оптико-физическим измерениям, лазерной технике, волоконной и интегральной оптике, компьютерным технике и технологиям, оптико-электронным средствам массовой информации, экологии, иностранному языку, основам менеджмента.
Александр Леонидович ДМИТРИЕВ
ОПТИЧЕСКИЕ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
Учебное пособие
В авторской редакции
Дизайн обложки С. А. Булгакова
Зав. Редакционно-издательским отделом Н. Ф. Гусарова
Лицензия ИД № 00408 от 05.11.99
Подписано к печати 2007 г.
Отпечатано на ризографе Тираж 100 экз. Заказ №