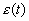 и магнитной восприимчивостью
и магнитной восприимчивостью 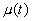 . На основе уравнений Максвелла и экспериментального закона Хаббла показано, что эти параметры могут изменяться во времени по экспоненциальному закону с относительным годовым изменением
. На основе уравнений Максвелла и экспериментального закона Хаббла показано, что эти параметры могут изменяться во времени по экспоненциальному закону с относительным годовым изменением МОДЕЛЬ КРАСНОГО СМЕЩЕНИЯ
Аннотация
Обсуждается новая модель космологического красного смещения на основе предположения постепенной эволюции физического вакуума, который рассматривается как реальная материя с зависящими от времени диэлектрической проницаемостью 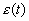 и магнитной восприимчивостью
и магнитной восприимчивостью 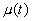 . На основе уравнений Максвелла и экспериментального закона Хаббла показано, что эти параметры могут изменяться во времени по экспоненциальному закону с относительным годовым изменением
. На основе уравнений Максвелла и экспериментального закона Хаббла показано, что эти параметры могут изменяться во времени по экспоненциальному закону с относительным годовым изменением
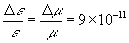 ,
,Рассматриваются связанные с этим космологические аспекты для объяснения некоторых свойств Вселенной.
I. Введение
В начале прошлого столетия было экспериментально установлено, что чем меньше светимость удаленных звезд и квазаров , тем больше сдвиг их спектральных линий в красную область спектра. Предполагая разумную светимость-расстояние функцию, Хаббл [1] обнаружил, что имеет место линейная зависимость между спектральным смещением и расстоянием до квазара L
|
|
(1) |
Здесь Z(L) – относительный спектральный сдвиг в красную сторону, lo – длина волны спектральной линии из спектра источника, который находится в лаборатории, неподвижной относительно Земли, lshift – длина волны той же линии на спектре квазара, наблюдаемого в той же лаборатории, а Ho – постоянная Хаббла и co – скорость света в вакууме. До настоящего времени такие спектральные наблюдения, дающие информацию о чрезвычайно удаленных объектах , являются единственным экспериментальным ключом для понимания истории Вселенной. Только такие гигантские расстояния (порядка1022 км) и временные интервалы (109 лет) способны выявить столь малые изменения, которые происходят с пока свет идет через пространство от источника до наблюдателя. Поэтому правильная интерпретация таких наблюдений для выяснения истинных механизмов красного смещения и понимания природы Вселенной является весьма важной задачей.
В настоящее время имеется несколько альтернативных моделей для объяснения красного смещения. Обычно его интерпретируют на основе эффекта Доплера, что в итоге приводит к понятию разбегания галактик и расширения Вселенной (модель Большого Взрыва). Однако в настоящее время эта интерпретация начинает вызывать сомнения. Действительно, кроме того, что до сих пор так и не нашли физически разумного объяснения сингулярности, обусловленной бесконечной плотностью материи в точке рождения Вселенной, скорости удаления вновь наблюдаемых звездных объектов, вычисленные в соответствии с этой интерпретацией, становятся неразумно большими. Например, для квазара Q01442+101 (при
Z=3,3) такая интерпретация приводит к значению его физической скорости приблизительно 0.9co.Более того, некоторые кластеры галактик очевидно старше возраста Вселенной , вычисленного в соответствии с этой моделью. Недавно экспериментально было установлено, что весьма обширные объекты (громадные слои галактик 200 миллионов световых лет поперек, 700 мл.св.л. в длину и 20 мл.св.л. толщиной) похожи на суперкластеры , ранее нанесенные на карту Б.Тулли [2]. Также были открыты еще более протяженные объекты (“космические лестницы”), простирающиеся на расстояния порядка семи миллиардов световых лет [3]. Поскольку измеренные в экспериментальной астрономии максимальные скорости космических объектов не превосходят 500км/с, то требуется по крайней мере 150 миллиардов св.л. для формирования таких структур, что в
несколько раз превосходит возраст Вселенной, вычисленный по модели БВ [3]. И ,наконец, после получения снимков очень удаленных объектов (Z порядка 4) при помощи космического телескопа “Хаббл”, когда должны были бы увидеть отдельные объекты ранней Вселенной, близкой к началу эволюции, выяснилось , что опять видны сложные образования (галактики). Ясно , что на формирования их структуры опять понадобилось бы огромное время, cоизмеримое с принятым по модели БВ возрастом Вселенной.Существует несколько альтернативных моделей красного смещения, основанных на идеях эволюции во времени либо фундаментальных физических констант (заряд и масса элементарных частиц, электромагнитная постоянная
co, постоянная Планка и т.п.), либо характеристик физического вакуума и света по мере его распространения из-за взаимодействия между ними. Изменение фундаментальных констант как возможная причина красного смещения широко обсуждалась с момента, когда Дирак выдвинул идею Больших Чисел [4]. Однако недавно было показано, что, по крайней мере, некоторые атомные константы не изменяются во времени. Например, недавно Потехин и Варшалович [5] изучили тонкое ращепление дублетов абсорбционных линий поглошения в спектрах квазаров. Они проанализировали 1414 дублетов (CIV, NV, CVI, MgII, AlIII, и SiIV) в широком диапазоне экспериментальных значений красных смещений (0,2< Z < 3,7). Анализ при этом не выявил каких либо статистически существенных изменений в постоянной тонкой структуры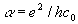 на временной шкале порядка 10 миллиардов св.л. Из этого можно заключить , что по крайней мере заряд электрона e, постоянная Планка h и электромагнитный коэффициент co следует считать именно постоянными. Что касается изменения массы элементарных частиц, эта идея обсуждалась ранее Х.Арпом [6] в модели intrinsic-redshift для доказательства , что природа красного смещения связана именно с возрастом объектов. Однако эта идея не подчиняется закону Хаббла (1) при постоянном значении
Ho [7]. Кроме того, постоянство массы электрона непосредственно следует из результатов работы [5]. Действительно, поскольку тонкое расщепление линий в спектрах разных объектов оказалось одним и тем же, а оно пропорционально постоянной Ридберга
на временной шкале порядка 10 миллиардов св.л. Из этого можно заключить , что по крайней мере заряд электрона e, постоянная Планка h и электромагнитный коэффициент co следует считать именно постоянными. Что касается изменения массы элементарных частиц, эта идея обсуждалась ранее Х.Арпом [6] в модели intrinsic-redshift для доказательства , что природа красного смещения связана именно с возрастом объектов. Однако эта идея не подчиняется закону Хаббла (1) при постоянном значении
Ho [7]. Кроме того, постоянство массы электрона непосредственно следует из результатов работы [5]. Действительно, поскольку тонкое расщепление линий в спектрах разных объектов оказалось одним и тем же, а оно пропорционально постоянной Ридберга 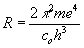 , то можно заключить, что и масса электрона
, то можно заключить, что и масса электрона
Из других моделей красного смещения, удовлетворяющих закону Хаббла, известны модели, основанные на идее постепенного изменения характеристик световой волны по мере ее распространения на гигантские расстояния в течение очень длительного времени. Такие изменения могут происходить благодаря взаимодействию света с веществом, рассеянным в космосе, (в том числе и с самим физическим вакуумом). Красное смещение при таком взаимодействии , как считают , могло бы быть вызвано либо постепенной потерей энергии фотоном благодаря поглощению (широко известная модель старения фотона, см. например, [8]), либо движением света без поглощения, но с изменением скорости из-за эволюции самого взаимодействия [9,10]. Идея старения фотона, однако, приводит к принципиальному противоречию между квантовым и классическим (на основе уравнений Максвелла) его описаниями. Фактически, предполагая , что энергия одиночного фотона в соответствии с квантовым подходом постепенно уменьшается вместе с уменьшением частоты по мере движения его через пространство , можно утверждать , что интенсивность светового потока из
N таких фотонов также постепенно падает. С точки зрения электродинамики это означает, что напряженность поля E постепенно уменьшается при одновременном уменьшении частоты. Однако нетрудно убедиться (см.Приложение), что не существует решения с одновременным уменьшением E(x) и w(x) с ростом х для волнового уравнения со стационарными граничными условиями , которое широко используется в физической оптике, электродинамике и квантовой электронике для адекватного описания любых процессов распространения света с постоянной скоростью в любых средах, в том числе и в физическом вакууме. Это позволяет считать идею старения фотонов несостоятельной, несмотря на привлекательность такого физического подхода.В настоящее время установлено, что вакуум не пустота, а является некой материальной средой с определенными, но еще не установленными свойствами. Это было подтверждено наблюдением вакуумных эффектов, например, нулевых колебаний и поляризации вакуума, генерации частиц в вакууме при электромагнитных взаимодействиях. Поэтому резонно предположить ,что физический вакуум может обладать внутренним трением из-за его малой, но реальной вязкости, что и может являться причиной изменения взаимодействия света с ним и в конечном счете приводить к красному смещению. Поскольку скорость света зависит от характеристик среды (физического вакуума)
таких, как co ,e и m , которые в принципе могут быть время/ пространственными функциями, она может быть не постоянна в этой среде. Это и может служить причиной красного смещения. Например, ситуация с пространственно зависимыми e(x) и m(x) для физического вакуума при постоянном электромагнитном параметре co , который связывает магнитные и электрические явления , но был идентифицирован со скоростью света в вакууме исторически, обсуждалась в [9]. Здесь рассматривалось волновое уравнение с учетом влияния затухания из-за трения вакуума. Решение этого уравнения, дающее постепенное увеличение длины волны (красное смещение) и изменение скорости света, обладает , однако, недостатком , так как требует считать e(x) и m(x) скорее параметрами взаимодействия , чем характеристиками среды. Это неудобство было преодолено в [10], где тот же результат был получен при постоянных e(x) и m(x) , но пространственно зависимом коэффициенте co. Однако и эту модель можно стало считать несостоятельной после заключения о неизменности параметра co, сделанного после появления работы [5] .В настоящей работе рассматривается более перспективная модель красного смещения, которая позволяет соединить электродинамический подход с космологическим принципом и эмпирическими результатами астрономии для объяснения некоторых особенностей реальности.
II. Эволюция параметров физического вакуума и модель красного смещения
Эта модель основана на классической электродинамике при предположения постепенной эволюции физического вакуума, который рассматривается как реальная материя с зависящими от времени диэлектрической проницаемостью 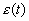 и магнитной восприимчивостью
и магнитной восприимчивостью 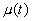 [11]. При этом будем считать, что изменение физических параметров вакуума происходит в соответствии с космологическим принципом одновременно и идентично в любой точке бесконечной развивающейся Вселенной. Тогда диэлектрическая проницаемость и магнитная восприимчивость вакуума в момент, когда свет покидает удаленный квазар в одной точке пространства, будут отличаться от значений , которые они примут , когда свет достигнет земного наблюдателя в другой точке пространства, что и может служить причиной красного смещения. Рассмотрим это более детально, записав уравнения Максвелла для плоско-поляризованной монохроматической волны, распространяющейся вдоль оси ОХ
[11]. При этом будем считать, что изменение физических параметров вакуума происходит в соответствии с космологическим принципом одновременно и идентично в любой точке бесконечной развивающейся Вселенной. Тогда диэлектрическая проницаемость и магнитная восприимчивость вакуума в момент, когда свет покидает удаленный квазар в одной точке пространства, будут отличаться от значений , которые они примут , когда свет достигнет земного наблюдателя в другой точке пространства, что и может служить причиной красного смещения. Рассмотрим это более детально, записав уравнения Максвелла для плоско-поляризованной монохроматической волны, распространяющейся вдоль оси ОХ
|
|
(2) |
Представление плоской волны здесь обосновано тем, что квазар является точечным источником, удаленным практически на бесконечность. Простейшим путем для решения задачи при зависимостях 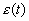 и
и 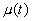 является запись волнового уравнения для волны индукции
является запись волнового уравнения для волны индукции
Волновое уравнение для индукции может быть получено из (2) путем цепочки подстановок
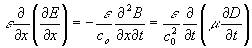 ,
,
выведенных из (2) путем взятия частной производной по х от левой части первого уравнения и использования второго уравнения.
В итоге мы имеем уравнение для злектрической индукции
|
|
(3) |
с граничными и начальными условиями:
при x = 0 и t = ts ( ts – начальный момент, когда свет покидает удаленный источник) D(0,ts) = e
(ts)E(0,ts), где E(0,ts) = Eoexpwots - напряженность злектрического поля монохроматической спектральной компоненты в волновой зоне, при постоянной амплитуде и частоте.Из уравнения (3) видно, что скорость волны индукции при распространении в физическом вакууме является функцией времени
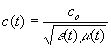 .
.
Чтобы найти конкретный вид этой зависимости, решение уравнения (3) будем искать в форме квази-периодической функции с переменной фазой
|
|
(4) |
Поскольку индукция по определению является напряженностью электрического в пустоте, где отсутствует какое-либо реальное вещество, в том числе и физический вакуум, то в пустоте нет поглощения. Поэтому амплитуду волны индукции а в (4) можно считать постоянной. После дифференцирования (4), подстановки в (3) и разделения реальной и мнимой частей мы получаем два уравнения
|
|
(5) |
где 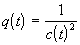 и
и 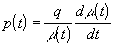
Чтобы иметь временные зависимости как для диэлектрической проницаемости, так и для магнитной восприимчивости, нам следует получить уравнение и для магнитной индукции. После дифференцирования по
x левой части второго уравнения в (2) и соответствующих подстановок при использовании первого уравнения можно получить точно такое же уравнение как (3) , но при B вместо D и e вместо m в скобках третьего члена. Очевидно и решение этого уравнения для В формально будет точно такое же, как (5) ,только при замене в нем m на e в определении p(t). Используя это заключение, т.е. p(t, e)= p(t, m), и определение скорости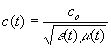 , мы получим соотношение
, мы получим соотношение
|
|
(6) |
где
Q –еще пока неизвестная функция времени, которая будет найдена позже. Принимая (6) во внимание, мы можем переписать (5) в виде|
|
(7) |
Из (6) видно, что поведение скорости света, проницаемости и восприимчивости
во времени одинаково в любой точке пространства, т.е. соответствует космологическому принципу. Это означает, что наблюдатель в конкретной точке на пути световой волны будет воспринимать эту волну как периодическую функцию, период которой зависит от скорости волны в данную эпоху временного развития. Другими словами
, частота света, воспринимаемая наблюдателем, зависит только от времени. Поэтому фазу можно записать в виде f(x,t)=V(t)±h(x). Подставляя это в первое уравнение (7), получаем|
|
(8) |
Здесь параметр 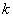 – константа, поскольку правая часть первого уравнения (8) зависит только от времени,а левая только от х.
– константа, поскольку правая часть первого уравнения (8) зависит только от времени,а левая только от х.
Из решения уравнения (8) следует, что
h(x) является линейной функцией x , т.е. h(x)=±kx+fo . Нетрудно убедиться, что это решение удовлетворяет и второму уравнению (7). Таким образом, параметр k , который является пространственной производной от фазы, есть ничто иное, как пространственная частота, т.е. хорошо известное в оптике волновое число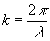 . После взятия интеграла от левой части (8) для фазы мы имеем
. После взятия интеграла от левой части (8) для фазы мы имеем
|
|
(9) |
Таким образом, мы приходим к важному заключению: электрическая индукция (соответственно, и световая волна) распространяется в вакууме с сохранением длины волны даже в случае зависимости параметров вакуума от времени, т.е. является пространственно стабильным образованием.
Эта длина волны задана граничными и начальными условиями вблизи удаленного квазара в момент, когда свет покидает его
|
|
(10) |
где ts - начало движения световой волны (момент излучения любой спектральной компоненты с частотой wo), c(ts) – скорость света в конкретную эпоху эволюции Вселенной. При этом частота атомного перехода wo является инвариантом, т.е. независимой характеристикой конкретного излучающего атома.
Что касается частоты света, воспринимаемой наблюдателем, то она может быть определена при использовании (9) как
w(t)=¶f/¶t при известной функции c(t). При этом последняя может быть найдена из (6) при известном значении Q(t) . Для нахождения Q(t) обратимся к закону Хаббла (1). Здесь расстояние, пройденное светом до наблюдателя, зависит как от ts, так и от эпохи на момент его наблюдения на Земле to|
|
(11) |
Принимая это во внимание, мы можем записать выражение (1) в виде
|
|
(12) |
где длина волны света при t = ts - определяется выражением (10) , а для света эталонного источника сравнения уже в нашу эпоху to
|
|
(13) |
В интегральном уравнении (12) скорость света co = c(to) и параметр
Ho измерены в нашу эпоху to. Для разных удаленных объектов, наблюдаемых в это время, будут различны времена 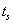 . Поэтому в (12) переменной интегрирования можно выбрать
. Поэтому в (12) переменной интегрирования можно выбрать 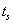 . После замены
. После замены 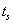 на
на 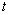 и дифференцирования (12) после предварительного использования в нем (10) и (13) можно получить простое дифференциальное уравнение для скорости света
и дифференцирования (12) после предварительного использования в нем (10) и (13) можно получить простое дифференциальное уравнение для скорости света
|
|
(14) |
Этот результат находится в соответствии с (6) при условии
Q=-Ho , т.е. при постоянном значении Q . После решения этих уравнений для наших начальных условий в области ts < t < to мы получаем экспоненциальный закон для скорости света, диэлектрической проницаемости и магнитной восприимчивости вакуума|
|
(15) |
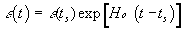
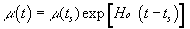
Используя (15) в правой части (8) при начальном условии (10) и k=2p/l (ts) , мы получаем зависимую от времени часть фазы в области ts < t < to в виде
|
|
(16) |
Поскольку производная от этой фазы по времени есть частота, воспринимаемая наблюдателем, то после дифференцирования можно получить для нее выражение
|
|
(17) |
Таким образом, волна индукции, которая распространяется с постоянной амплитудой и длиной волны, детектируется оптическим детектором как сигнал с изменяющейся во времени частотой из-за постепенного изменения параметров вакуума.
Что касается поведения напряженности поля световой волны, то она может быть получена из последнего материального уравнения в (2) с учетом (4), (15) и начальных условий в уравнении (3) в виде
|
|
(18) |
где, как видно, амплитуда электрического поля затухает во времени. Однако оно не связано с поглощением энергии, как это предполагается в модели старения фотона, а является следствием эволюции физического вакуума. Общее выражение для фазы световой волны из (9) и (15) имеет вид
|
|
(19) |
Теперь эти выражения (10), (17), (18) и (19) в зависимости от ситуации мы можем использовать для расчета характеристик света от удаленного и земного источников. Например, для сравнения их длин волн в нашу эпоху мы должны положить t = to в формулах (15), (17) и можем получим следующее.
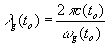 при скорости света в нашу эпоху c(to) = co и воспринимаемой наблюдателем частоте
при скорости света в нашу эпоху c(to) = co и воспринимаемой наблюдателем частоте 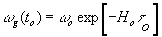 , где
, где
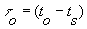 - так называемое время обратного взгляда (look-back time)
- так называемое время обратного взгляда (look-back time) 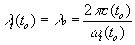 , где частота его излучения w (to) = wo, так как практически нет интервала времени между излучением и наблюдением, т.е.
, где частота его излучения w (to) = wo, так как практически нет интервала времени между излучением и наблюдением, т.е. 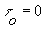 .
.
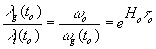
Хотя длина волны от квазара больше длины волны эталонного источника и мы привыкли говорить о красном смещении, на самом деле физически происходит постепенное смещение длины волны земного источника со временем (при смене эпохи скорость света уменьшается при сохранении частоты атомного перехода wo), но в фиолетовую область спектра.
Таким образом, при сохранении прежней терминологии имеет место красное смещение 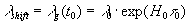 . При этом вместо потери энергии из-за поглощения при одновременном уменьшении частоты и сохранении скорости света , как это имеет место в модели старения фотона, рассматриваемый здесь механизм имеет другую физическую интерпретацию. Она основана на постепенном изменении параметров физического вакуума. Вызванное этим постепенное уменьшение напряженности светового поля по мере его распространения в таком вакууме сопровождается сохранением длины волны и уменьшением скорости света.
. При этом вместо потери энергии из-за поглощения при одновременном уменьшении частоты и сохранении скорости света , как это имеет место в модели старения фотона, рассматриваемый здесь механизм имеет другую физическую интерпретацию. Она основана на постепенном изменении параметров физического вакуума. Вызванное этим постепенное уменьшение напряженности светового поля по мере его распространения в таком вакууме сопровождается сохранением длины волны и уменьшением скорости света.
III. Космологический аспект
Космологический принцип о тождественности любых точек Вселенной позволяет экстраполировать уравнения (15) от момента наблюдения ts на всю временную шкалу как в прошлое, так и в будущее. Если принять нашу эпоху за начало координат, то скорость света в (15) может быть записана в виде
|
|
(20) |
где t < to определяет историю до нашей эпохи, а для t > to мы имеем будущее Вселенной. Экспоненциальная зависимость подразумевает отсутствие каких-либо особенностей на временной шкале. Все изменения параметров Вселенной не имеют начала или конца, т.е. происходят везде и всегда идентично. Эти изменения очень малы. Например, как следует из
(20) при co = 3Ч108m/s и известном значении постоянной Хаббла Ho=100kms-1Mpc-1, т.e. 2,9Ч10-18s-1, скорость света в вакууме изменяется на 2,7 m/s за 100 лет. Недавно Монтгомери и Долфин [12] выполнили статистический анализ практически всех экспериментов по измерению скорости света и обнаружили, что ее измеренные значения на уровне статистики слегка уменьшились за 250 лет. Это позволяет надеяться, что при повышении точности эксперимента и по прошествии времени, достаточного для получения существенных изменений параметров вакуума, предлагаемая здесь модель красного смещения, может быть проверена экспериментально.Такой подход позволяет построить космологию с бесконечной Вселенной, которая всегда существовала и везде однородна. Использовав (11) и (15), мы можем найти расстояние r, пройденное светом к любому моменту времени после старта в момент ts
|
|
(21) |
В отличие от моделей с постоянной скоростью света, здесь мы видим, что это расстояние нелинейно
изменяется во времени и асимптотически приближается к пределу в определенном интервале 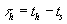 . Уже при
. Уже при 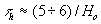 вторым членом можно пренебречь и практически достигается предел
вторым членом можно пренебречь и практически достигается предел
|
|
(22) |
Это предельное расстояние обусловлено затуханием напряженности электрического поля (19) и может быть интерпретировано как пространственный космологический горизонт для света в вакууме. С учетом этого горизонта фотометрический парадокс Ольберса [13] получает естественное объяснение. Действительно, если Земля находится вне этих световых горизонтов, то свет от далеких объектов просто не достигает Земли. Другими словами, земной наблюдатель видит только некоторые
удаленные образования, горизонты которых во временных единицах больше времени обратного взгляда to = to - ts, т.e. для to<th . Интересно, что чем раньше был испущен свет, когда больше была скорость света, тем больше был горизонт для квазаров, связанных с более ранней Вселенной. Используя (20) при t = ts и (21) при t = to в выражении (1) , где L = L(to) = r(to мы получаем для относительного спектрального сдвига|
|
(23) |
Как следует из оценки при 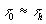 может достигаться максимально возможное значение для горизонта
может достигаться максимально возможное значение для горизонта

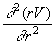 справедливо для любой функции V(r), где радиус сферической волны-
справедливо для любой функции V(r), где радиус сферической волны- 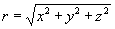 (см.,например, [14]). Поэтому индукцию D в уравнении (3) мы можем заменить произведением (rD) без изменения уравнения (при совпадении направления светового луча r с осью x).
(см.,например, [14]). Поэтому индукцию D в уравнении (3) мы можем заменить произведением (rD) без изменения уравнения (при совпадении направления светового луча r с осью x).
Таким образом. в волновой зоне (r>>l/2p ) мы получаем индукцию в виде сферической волны, для которой напряженность электрического поля имеет вид
|
|
(24) |
а интенсивность
|
|
(25) |
Для оценки степени затухания с расстоянием и в зависимости от времени обратного взгляда to используем (15) и (21) при t = to. После подстановки параметров нашей эпохи co, eo и L(to) = r(to) в (25) мы имеем
|
|
(26) |
где 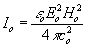 .
.
Сравним это с интенсивностью этой волны, взятой для какой-нибудь предыдущей точки 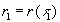 оптического пути
оптического пути 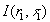 , где
, где 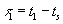 . Расстояние
. Расстояние 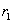 возьмем много короче
L(to), но достаточным, чтобы рассматривать квазар как точечный объект. Тогда отношение
возьмем много короче
L(to), но достаточным, чтобы рассматривать квазар как точечный объект. Тогда отношение 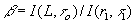 может быть получено в виде
может быть получено в виде
|
|
(27) |
Здесь при разложении экспоненты в ряд из-за 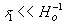 мы оставили только первый член. В соответствии с современными измерениями постоянная Хаббла имеет значение в интервале 60-140 kms-1Mpc-1. Использовав Ho = 100km s-1Mpc-1 и t1 = 5Ч 106 лет (при r1 =100d, где d - размер типичной галактики, примерно 50 kps) , мы получаем таблицу значений
b(to) для разных
мы оставили только первый член. В соответствии с современными измерениями постоянная Хаббла имеет значение в интервале 60-140 kms-1Mpc-1. Использовав Ho = 100km s-1Mpc-1 и t1 = 5Ч 106 лет (при r1 =100d, где d - размер типичной галактики, примерно 50 kps) , мы получаем таблицу значений
b(to) для разных 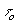 .
.
В последней колонке для сравнения приведены данные, полученные на основе модели с постоянной скоростью света, т.e. bc = (t1/to)2.
Таблица
|
t o (look-back time) |
Z (redshift) |
b (at variable c) |
b c(at constant c) |
|
H o-1= 1.08Ч1010years |
1.8 |
1.5 Ч10-11 |
2 Ч10-7 |
|
2Ho-1 |
6.8 |
1.2 Ч10-13 |
5 Ч10-8 |
|
3Ho-1 |
21 |
2.1 Ч10-15 |
2.2 Ч10-8 |
|
4Ho-1 |
60 |
3 Ч10-17 |
1.2 Ч10-8 |
|
5Ho-1 |
170 |
4.5 Ч10-19 |
8 Ч10-9 |
|
6Ho-1 |
480 |
7 Ч10-21 |
5 Ч10-9 |
|
|
|
|
|
Отсюда видно, что для случая с изменяющейся скоростью света интенсивность падает более резко, особенно при больших Z , по сравнению с обычной моделью. Это очевидно сильно ограничивает видимый горизонт и при чувствительности современной аппаратуры практически делает невозможным измерение Z более 6. Фактически квазар с наибольшим значением красного смещения (Z=5) недавно наблюдали на телескопе Subaru.
IV. Заключение
Обсуждается новая модель космологического красного смещения на базе классической электродинамики и экспериментального закона Хаббла. Полученное волновое уравнение (3) в отличие от обычного имеет третий член, учитывающий взаимодействие света с физическим вакуумом как реальной средой. Из решения этого уравнения следует, что свет распространяется в вакууме с сохранением длины волны (10) и изменением скорости (15) из-за постепенной эволюции вакуума с относительной годовой скоростью изменения параметров 10-10.
Фактически из-за такой эволюции, за огромное время нахождения света в пути от квазара до Земли уменьшается длина волны эталонного источника на Земле по сравнению с длиной волны прибывшего от удаленного объекта света. Другими словами, при принятии за начало координат нашей эпохи мы имеем красное смещение для света от квазара при его наблюдении на Земле. Эта модель позволяет объяснить кроме природы красного смещения также и другие свойства реальности, например, парадокс Ольберса и ограничение в наблюдении большого относительного спектрального сдвига Z.
ПРИЛОЖЕНИЕ
Для изучения распространения света с постоянной скоростью в любой среде обычно используют волновое уравнение со стационарными условиями [14]
|
|
(1A) |
at E(0,t)=Eoexp wo t и 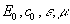 - constant
- constant
Как это делают в модели старения фотона будем считать, что длина волны зависит от пройденного расстояния и искать решение в форме квази-периодической функции с переменной фазой и
x-зависимой амплитудой|
|
(2A) |
Подставляя это в уравнение и разделяя мнимую и реальную части, получим
|
|
(3A) |
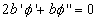
Принимая во внимание 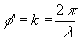 , перепишем второе уравнение в (3A) в виде
, перепишем второе уравнение в (3A) в виде
|
2b'l-bl'=0 |
(4A) |
Отсюда следует
|
b/l=2b'/l |
(5A) |
Поскольку левая сторона всегда положительна, знаки производных в правой стороне должны быть одинаковы. Отсюда следует, что может иметь место красное смещение (при
l'>0) , но лишь при увеличении амплитуды (при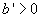 ), что не реально. Либо может иметь место фиолетовое смещение (l'<0) при уменьшении амплитуды (
), что не реально. Либо может иметь место фиолетовое смещение (l'<0) при уменьшении амплитуды (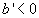 ), что не соответствует эксперименту.
), что не соответствует эксперименту.
Таким образом, модель старения фотона не может быть принята как реальная, так как не удовлетворяет волновому уравнению, адекватно описывающему любые процессы распространения света в любых средах.
Ссылки
[1] E. P. Hubble, Proc. Nat. Acad. Sci. 15, 168 (1929).
[2] R. Brent Tully, Astrophysical Journal,303,25(1986).
R. Brent Tully, J. R. Fisher, Atlas of Nearby Galaxies, (Cambridge: Cambridge University Press, 1987)
[3] E. J. Lerner, The Big Bang never happened, (Simon & Schuster Ltd, London, 1992).
[4] P. A. M. Dirac, Nature 139, 323 (1937).
[5] A. Potekhin, D. Varshalovich, Astronomy and Astrophysics Supplement 104, 89 (1994).
[6] H. Arp, Progress in New Cosmologies, (Plenum Press, New York, 1, 1993).
[7] H. Arp, Quasars, Redshifts and Controversies, Interstellar Media, (Berkeley, 1987).
[8] L. De Broglie, Cahiers de Physique, 16, 425 (1962).
[9] E. I. Shtyrkov, Gal. Electrodynamics, 3, 66 (1992).
[10] E. I. Shtyrkov, Progress in New Cosmologies, Plenum Press, New York, 327 (1993).
[11] E. I. Shtyrkov, Gal. Electrodynamics, 8, 3, 57 (1997).
[12] A. Montgomery, L. Dolphin, Gal. Electrodynamics 5, 93 (1993).
[13] H. W. M. Olbers, Edinburg New Philosophical Journal, 1, 141 (1826).
[14] M. Born, E. Wolf, Principles of optics, (Pergamon Press, New York, 1964)