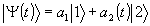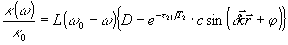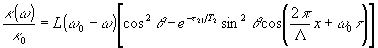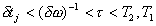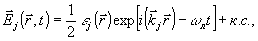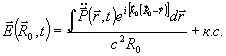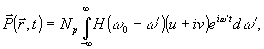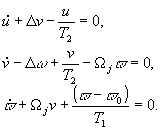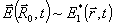ШТЫРКОВ Е И - ДИНАМИЧЕСКАЯ ЭХО-ГОЛОГРАФИЯ

ДИНАМИЧЕСКАЯ ЭХО-ГОЛОГРАФИЯ

профессор Е. И. Штырков

Обсуждается новое направление в голографии, основанное на явлении интерференции атомных когерентных суперпозиционных состояний, индуцируемых в резонансной среде разнесенными во времени объектным и опорными оптическими импульсными полями.

1. Введение

Прежде всего следует дать определение, что такое динамическая эхо-голография (ДЭГ). Под этим понятием будем подразумевать такую запись и восстановление волновых фронтов света, когда опорные, объектные и восстановленные волны не совпадают во времени. При такой ситуации, когда опорное и объектное импульсные поля разнесены во времени настолько, что даже не перекрываются в пространстве, они не могут интерферировать в веществе друг с другом непосредственно. В работе [1] впервые было показано, что информация о волновом фронте объектного поля, тем не менее, может быть восстановлена спустя некоторое определенное время после воздействия на резонансную регистрирующую среду. При определенных условиях возбуждения атомной системы в условиях резонанса эта система может излучать когерентный отклик, волновой фронт которого зависит не только от формы волновых фронтов объектного и опорного полей, но и от порядка подачи этих полей на регистрирующую среду. Физические основы, заложенные в таком типе голографии (ДЭГ), базируются на необходимом сочетании двух явлений. Во-первых, это интерференция суперпозиционных состояний, индуцируемых при когерентном возбуждении коллектива атомов. Во-вторых, необходимо, чтобы после возбуждения коллектив атомов обладал достаточно длинной "фазовой памятью" о таком возбуждении. Остановимся более подробно на первом. Рассмотрим для начала одиночный атом. Известно, что любой атом может находиться не только в своих стационарных состояниях, т.е. на так называемых, энергетических уровнях, но также и в линейной суперпозиции этих состоянии. Стационарные состояния атома при отсутствии внешних воздействий на него являются решением стационарного уравнения Шредингера для волновой функции атома и являются устойчивыми. При этом все возбужденные энергетические уровни атома, кроме основного состояния, квазиустойчивы в том смысле, что достаточно малейшего влияния со стороны окружения атома (внешние электрические и магнитные поля, столкновения, фононные колебания и т.п.) и атом, выведенный из этого состояния, релаксирует к основному уровню. При этом в течение этого переходного процесса атом последовательно проходит непрерывный спектр суперпозициоиных состояний соответствующих данному энергетическому переходу. Обычно такие состояния определяют волновой функцией, зависящей от времени:

(1)

где |1> и |2> - собственные волновые функции, соответствующие нижнему и верхнему уровням энергии. Амплитуды вероятности

являются гармоническими функциями от времени. Основным свойством суперпозиционного состояния является его принципиальная неустойчивость. Атом, попавший каким-либо образом в это состояние, если на него уже ничто извне не влияет (например, отсутствуют внешние поля и подавлены различные причины релаксации), тем не менее, немедленно начинает возвращаться в равновесное состояние из-за наличия внутренних сил. Эта неустойчивость суперпозиционных состояний становится очень важной, когда мы переходим к рассмотрению согласованных колебаний целого коллектива атомов. Естественно, что на практике мы имеем дело с большим числом атомов и в голографии нас интересуют именно когерентные свойства ансамбля частиц. Возбудив ансамбль частиц когерентная образом, можно каждый атом из коллектива перевести в одно и то же суперпозиционное состояние. Такое состояние ансамбля является когерентным суперпозиционным состоянием, и его движение в дальнейшем будет в течение некоторого времени согласованным именно в силу неустойчивости состояния отдельного атома. Непосредственно после перевода атомов в это состояние каждый атом в одно и то же время начинает возвращаться к равновесию. Другими словами, все диполи будут иметь одинаковые начальные фазы. Естественно, что этого невозможно было бы достигнуть, если все атомы были переведены, пусть даже и когерентным образом, в одно из стационарных возбужденных состояний. Из этих состояний атомы могут переходить только под влиянием случайных внешних причин. Поэтому начальные фазы колебаний отдельных диполей не могут совпадать и чистое когерентное суперпозиционное состояние коллектива не может иметь места.

Динамическая эхо-голография основана на интерференции именно когерентных суперпозиционных состояний атомов. В определенных условиях после когерентного возбуждения коллектив атомов может обладать достаточно длинной "фазовой памятью" о когерентности возбуждающих полей. В течение переходного процесса когерентные суперпозиционные состояния постепенно разрушаются из-за различных процессов релаксации и коллектив атомов постепенно переходит в смешанное состояние, характеризуемое отсутствием "фазовой памяти". Хотя в этом состоянии каждый атом обладает дипольным моментом, макроскопическая поляризация среды, обусловленная когерентными коллективными колебаниями, исчезает и остается только спонтанная часть поляризации. Интенсивность спонтанного излучения системы атомов в этом случае в N раз меньше интенсивности, обусловленной когерентной частью поляризации (N - плотность активных центров в веществе). В различных веществах концентрация активных центров достаточно велика (10⁸ - 10²⁰ см^-3). Поэтому легко себе представить, насколько эффективнее протекают процессы взаимодействия света с веществом на стадии той части переходного процесса, где "фазовая память" атомной системы еще не нарушена и в веществе могут иметь место различные переходные квантовые оптические явления, так называемые транзиент-эффекты типа самоиндуцированной прозрачности [2], оптической нутации [3], фотонного эха [4], сверхизлучения [5], индуцирования пространственных решеток в веществе разнесенными во времени оптическими полями [6,7] и др. [8]. Остановимся на причинах нарушения "фазовой памяти" системы.

Память о когерентности возбуждения, как мы уже говорили, есть свойство целой группы атомов, а не отдельного излучателя. Если ансамбль состоит из атомов с одной и той же собственной частотой излучения, то при отсутствии каких-либо причин релаксации разность фаз колебаний отдельных диполей со временем сохраняется до конца переходного процесса, пока все атомы не перейдут в равновесное состояние. Однако всегда существуют какие-либо внешние воздействия, которые сбивают фазу колебании отдельных диполей путем статистического случайного изменения мгновенного значения собственной частоты колебаний диполя. Такие изменения происходят необратимым образом, одинаковы для каждого атома и приводят к однородному уширению спектра излучения всего коллектива. Это уширение обуславливает спад макроскопической поляризации среды из-за постепенного выхода отдельных атомов из согласованного излучающего коллектива. Таким образом, фазовую память системы в этом случае можно характеризовать обратной величиной однородного уширения данного атомного перехода. Однородное уширение при этом складывается из естественного радиационного уширения и части, обусловленной влиянием различных внешних воздействий. Поэтому для уменьшения однородного уширения, а следовательно, для удлинения "фазовой памяти" необходимо подавлять влияние внешних причин. Например, охлаждением кристалла от комнатной до низких температур (десятки °К) можно удлинить память однородно уширенного ансамбля от 10^-13 c до 10^-7 с . На практике гораздо чаще - встречается ситуация, когда ансамбль уширен неоднородным образом. В этом случае расфразировка макроскопической поляризации обусловлена не только статистическими изменениями собственной частоты, но и набегом фаз δωt в течение времени t, где δω - разброс частот излучающих диполей (либо это разброс собственных частот отдельных атомов, как, например, в кристаллах из-за локальных неоднородностей внутрикристаллического поля, либо разброс, обусловленный эффектом Допплера в газах). Процесс этой расфазировки макроскопической поляризации может быть обращен в какой-то момент времени и поляризация может быть восстановлена.Это свойство обратимости используется для генерирования когерентных откликов атомной системой [9].

Например, после воздействия на систему двух или более импульсов когерентного света она излучает сигнал фотонного эха [4]. Это эхо является аналогом спинового ядерного эха [10] и в настоящее время используется для измерения релаксационных характеристик атомных переходов. Первичное или, как его называют, двухимпульсное фотонное эхо - это поле, излучаемое атомной системой которое возникает после подачи второго импульса, а время его задержки совпадает с интервалом, разделяющим два первые импульса накачки. Другая разновидность фотонного эха - это стимулированное эхо (трехимпульсное эхо). Этот когерентный отклик системы на действие трех поочередных импульсов возникает после третьего импульса спустя также время, равное раздвижке между двумя первыми импульсами.

2. Преобразование волновых фронтов в сигналах фотонного эха

Вопрос о возможности записи восстановления и преобразования волновых фронтов в геометрии опыта по фотонному эху был впервые рассмотрен в работе [1], где и был введен термин "эхо-голография". Аналогичные предложения были сделаны затем в работах [11,12].

Для начала рассмотрим 2-х уровневую систем у атомов, неоднородным уширением которой можно пренебречь. Во многих практических случаях оптические переходы можно изучать в рамках двухуровневой модели атома, и плодотворность такого подхода доказана в настоящее время на многих примерах. Пусть на однородно уширенную систему атомов действуют два разнесенных во времени коротких импульса монохроматического света. Если задержка между импульсами τ₂₁ меньше времени необратимой фазовой релаксации Т₂, то, как было показано в работах [6,7,13], во время действия второго импульса на атомном переходе индуцируется пространственная решетка-голограмма, глубина модуляции которой зависит от степени потери "фазовой памяти" к моменту прихода второго импульса. Относительный коэффициент поглощения среды в этом случае, когда длительность импульсов мала настолько, что релаксацией во время действия отдельных импульсов можно пренебречь, для t > τ₂₁ будет иметь вид [14]:

(2)

где L(ω₀-ω) - форма линии однородного уширения;

D, С, φ - коэффициенты, зависящие от расстройки от резонанса Δ=ω_л-ω₀, (ω_л, ω₀ - частоты, соответственно, накачки и атомного перехода) и "импульсных площадей" накачки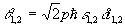 (p - дипольный момент перехода, ε, δt - амплитуды и длительности полей накачки). При идентичности накачки θ₁=θ₂=θ β случае точного резонанса, например, мы имеем довольно простое выражение:

(3)

где шаг решетки 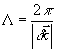можно варьировать путем изменения угла между первым и вторым пучками накачки . В случае, когда волновые фронты, импульсов накачки отличны от плоских, решетка (2) содержит фазовую информацию об этих фронтах, т.е. является голограммой /6,13/. Мы не будем далее подробно останавливаться на особенностях процесса формирования решеток, т.к. он достаточно подробно исследовался в работе /14/. Отметим только, что в случае, когда система атомов уширена теперь уже неоднородным образом, в среде индуцируется уже не одна, а целая серия бегущих решеток, направление и скорость движения которых зависят нелинейным образом от расстройки от резонанса, а амплитуды решеток пульсируют во времени с удвоенной обобщенной частотой Раби, соответствующей второму импульсу накачки. После того, как действие второго импульса накачки заканчивается, движение решеток прекращается и в среде замораживается сложная интерференционная картина. Следует, однако, подчеркнуть, что эта картина, хотя и остается неподвижной в пространстве, со временем распадается. На отрезке времени t>Т₂ все фазовые коллективные соотношения усредняются и распад решеток на этом этапе определяется только энергетическими характеристиками перехода. Этот распад происходит со временем продольной релаксации Т₁ /6/, которое определяет стремление системы к термодинамическому равновесию. Как в случае однородного, так и неоднородного уширения перехода информация из такой голограммы может быть извлечена при помощи слабой пробной волны, как и в обычных голограммах. Однако, неоднородноуширенная система, способная генерировать когерентный отклик самостоятельно, позволяет восстановить фазовую информацию в сигналах первичного и стимулированного фотонного эха. Это становится возможным при выполнении условия

(4)

где δω - π разброс атомов в пределах полуширины "дыры выжигания" в спектре поглощения перехода (рис.1).

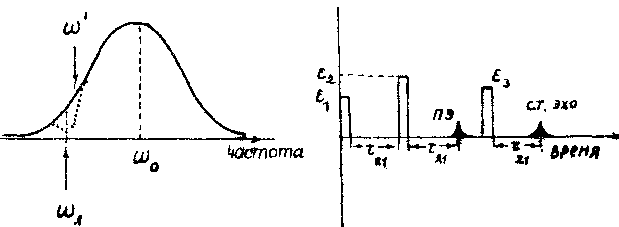
Рис.1. Условия возбуждения среды

Допустим, что двухуровневая атомная система возбуждается при условии (4) последовательностью трех импульсов когерентного света:

(5)

где j = 1,2,3 - индекс импульса. Если фазор волны выразить в виде 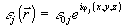, где φ(x,у,z)- слабое фазовое возмущение волнового фронта, то такие волны можно рассматривать как квазиплоские монохроматические волны частоты ω_л, что позволяет в дальнейшем получить более наглядную картину преобразования волновых фронтов в откликах системы. Действие сильного монохроматического поля приведет к поляризации целой группы атомов, собственные частоты которых локализованы в окрестности частоты ω_л (см. "дыру выжигания" на рис.1). Поле, излучаемое при этом образцом, можно найти в волновой зоне в виде

(6)

Здесь - удельная поляризация среды, наведенная полями 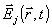. 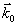- волновой вектор отклика системы, 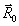- радиус-вектор точки наблюдения. Удельная поляризация после усреднения по статистическому ансамблю имеет вид:

(7)

где N - концентрация активных центров, - функция неоднородного уширения перехода. Поперечные компоненты вектора Блоха u и v могут быть найдены из решений оптических уравнений Блоха /8/:

(8)

Здесь эффективность воздействия поля на систему определяется резонансной частотой Раби , а продольная компонента псевдоспина (не путать с ω) характеризует поведение разности заселенностей уровней для одной произвольной изохроматы ω' (Δ=ω'-ω_л). Начальные условия в (8) определяются предысторией возбуждения. Например, во время действия первого импульса на систему, находящуюся до этого в термодинамически равновесном состоянии, u₀=v₀=0, а берется для Больцмановского распределения атомов по уровням. В промежутке между импульсами u₀ и v₀ отличны от нуля и являются решениями (8) на предыдущем этапе. Используя (7) и (8), а также предполагая возбуждение достаточно мощным, чтобы перекрыть всю гауссову линию, из (6) можно получить поле отклика системы для t>τ₂₁+δt₂ в виде квазиплоской волны с возмущением волнового фронта

(9)

где

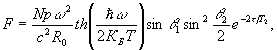
При расчете предполагалось, что длительность импульсов накачки мала (δt<<τ₂₁). Коэффициенты F, A(t), В достигают своего максимума при условиях: 90° - первый импульс накачки, а второй является 180°-импульсом, t=2τ₂₁, . При отклонении t от 2τ₂₁ коэффициент А(t)→0 и поле резко спадает со скоростью определяемой временем расфазировки Т₂^*=(δω)^-1. Таким образом, после второго импульса накачки спустя время τ₂₁ возникает когерентный импульс света - первичное эхо, который распространяется в направлении . Это поле содержит фазовую информацию о волновых фронтах обоих импульсов накачки. Форма волнового фронта эха зависит от порядка подачи этих импульсов. Рассмотрим частные случаи.

I. Первый импульс - объектная волна с фазовым возмущением φ₁=φ₁(х,y,z). Второй импульс - плоская опорная волна (φ_z=0). Тогда φ₀=-φ₁(x,y,z), т.е. эхо имеет волновой фронт, комплексносопряженный фронту объектной волны

(10)

II. Обратный порядок подачи импульсов: сначала действует плоская волна φ₁=0, затем объектная φ₂=φ₂(x,y,z). В этом случае первичное эхо имеет удвоенное фазовое возмущение φ₀=2φ₂(x,y,z) по сравнению с объектной волной. Это обстоятельство может быть использовано для повышения чувствительности интерферометрических измерений слабых фазовых неоднородностей (например, потоки газов при низких давлениях), подобно /15/, где фронт удвоенной кривизны формировался во втором порядке дифракции при восстановлении с голограммы, экспонированной нелинейным образом. Как мы видим, двухимпульсное эхо при любом порядке подачи импульсов не позволяет получить волновой фронт, совпадающий точно с фронтом объектной волны. Этого можно достигнуть только после воздействия на среду третьим импульсом. Такую ситуацию мы рассмотрим несколько позже. В случае слабых фазовых искривлений волнового фронта (квазиплоские волны) нетрудно характер восстановления фронтов в сигналах двухимпульсного эха пояснить простыми геометрическими соображениями. Допустим, что опорная и объектная волны распространяются в одном направлении (). Тогда эхо будет распространяться в этом же направлении (). Пусть объектная волна ε' действует раньше, чем опорная ε (рис.2а). Подходя к регистрирующей среде волна ε возбуждает атомы образца, находящиеся в разных участках среды, несколько в разное время. Например, при геометрии фронта, изображенного на рис.1, все частицы, расположенные в районе точки А возбуждаются раньше, чем вблизи точки В (рис.2б). Поскольку накачка этих частиц прекращается также раньше, то расфазировка колебаний диполей в этой области начнется также раньше, чем в районе точки В. Поэтому, к приходу плоской волны ε одновременно в точки А и В (рис.3в) расфазировка диполей в этих точках будет неодинакова. После прохождения волны ε, начнется процесс дефазировки диполей, и для диполей в точке А понадобится больше времени, чтобы сфазироваться и вызвать появление сигнала эха. Поэтому эхо в точке В возникнет раньше (рис.2г), это приведет к искривлению волнового фронта в противоположную сторону. За голограммой теперь уже будут распространяться три волны (рис.2д): ε', ε θ ε_э=ε'^*.

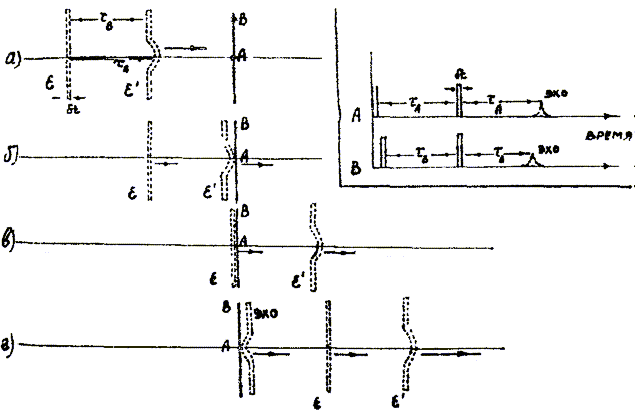
Рис.2. Обращение кривизны волнового фронта.

Рассмотрим обратную ситуации (рис.3), когда первой действует плоская волна ε. Здесь расфазировка во всех точках образца начнется одновременно, а процесс дефазировки в точке В будет задержан на время (τ_В-τ_А). Поэтому эхо в точке А возникнет на время 2(τ_В-τ_А) раньше, чем в точке В, что приведет к удвоению возмущения волнового фронта. Аналогичным образом могут быть объяснены и другие ситуации. Например, если фронты импульсов накачки самосопряжены (φ₁=-φ₂), то волновой фронт эха будет иметь утроенное возмущение обратной по отношению к первому импульсу кривизны (φ₀= -3φ₁). Такая простая геометрическая интерпретация возможна лишь в случае квазиплоских волн, распространяющихся в одном и том же направлении. Следует отметить, что при произвольной сложной форме волнового фронта первичное эхо может содержать искаженную информации об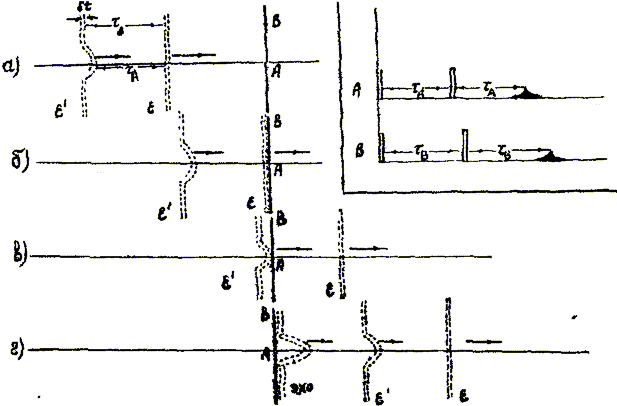

Рис.3. Удвоение фазового возмущения волнового фронта.

объектной волне, вследствие того, что высокочастотные пространственные компоненты Фурье-образа объектной волны могут не восстанавливаться в сигналах эха. Этот вопрос тоже подробно рассмотрен в работе /16/, уже было показано, что правильная передача волновых фронтов в случае первичного эха возможна лишь при углах между высшими пространственными частотами объектной волны и опорной волной, не превышающих 3°. Такое ограничение снимается в случае четырехволнового неодновременного взаимодействия (стимулированное фотонное эхо), т.е. когда нас интересует волновой фронт отклика системы на воздействие трех и более импульсов. Волновые фронты эха при таких взаимодействиях, как показано в /1/, также связаны с порядком подачи импульсов накачки. Например, в случае 3-х импульсного эха точное восстановление волнового фронта может бить обеспечено только в ситуации, когда сначала действует плоская (опорная) волна, затем объектная волна с произвольным волновым фронтом, а затем плоская считывающая волна, которая распространяется в том же направлении, что и первая (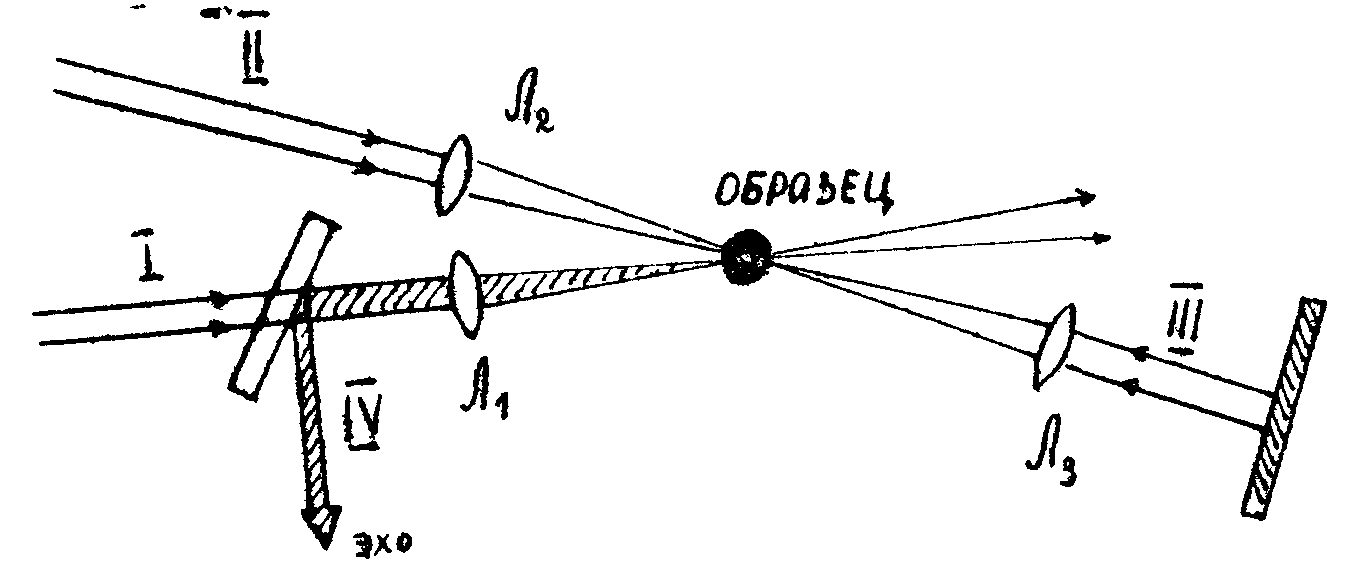). В сигнале стимулированного эха каждая η -компонента пространственного фурье-спектра объектной волны распространяется в направлении . В случае каждая компонента восстановится без искажения. В этом случае мы имеем дело с более общим по сравнению с традиционной голографией принципом записи и восстановления волновых фронтов, так как, кроме памяти о волновом фронте, такая голограмма запоминает как порядок подачи объектной и опорной волн, так и величину задержки объектной волны относительно опорной. Стимулированное эхо позволяет так же, как и первичное эхо, получить комплексносопряженную реплику объектной волны. Это будет иметь место, когда сначала действует объектная волна, а затем поочередно две плоские волны. При этом полное обращение волнового фронта может быть получено, если вторая и третья волны имеют точно противоположные направления (). При такой ситуации, аналогично одновременному четырехволновому взаимодействию, при наличии стоячей волны /17/ стимулированное эхо будет иметь направление и волновой фронт обращенными по отношении к объектной первой волне. Отличие будет заключаться лишь в том, что обращенная волна будет задержана во времени. Экспериментально обращение волнового фронта в геометрии фотонного эха впервые было продемонстрировано в работе /7/. Здесь наблюдалось обратное фотонное стимулированное эхо в рубине, помещенном с целью выполнения условия (4) в гелиевый криостат (~2°К). Резонанс наблюдался на переходе ⁴А₂(±1/2)-²Е() λ=6934 Å при накачке рубиновым лазером, работающим на другой компоненте дуплета этого же перехода ⁴А₂(±3/2)-²Е() λ=6933,97 Å. Обратное эхо наблюдалось в направлении IV (рис.4), в то время как третий импульс создавался отражением второго пучка (II) от плоского зеркала М. Сигнал эха в направлении IV имел ту же дифракционную расходимость, что и первый пучок (I), несмотря на то, что он проходит через линзу Л_I. Это говорит о том, что образец испускает волну, обращенную по отношению к I пучку. Поскольку зеркало М плоское, то опорный и считывающий пучки II и III также обращены по фронту и поэтому искажения фазы, вносимые этими пучками, вычитаются.

Рис.4. Схема эксперимента.

В заключение можно указать на некоторые возможные перспективы использования такого способа индуцирования динамических решеток. Прежде всего, вопрос формирования интерферограмм разнесенными во времени волнами имеет самостоятельное научное значение. Это обусловлено тем, что в теории интерферометрии, которая в настоящее время сложилась в классической оптике, рассматриваются лишь когерентные свойства самих оптических полей и не учитывается фазовая память регистрирующей среды. По-видимому, учет этого обстоятельства позволит значительно расширить и обобщить теорию интерферометрии, что, в свою очередь, будет способствовать развитию техники интерферометрических исследований. Следует также отметить, что преобразование волновых фронтов с запоминанием временных характеристик оптических полей может быть использовано в машинной обработке оптической информации и для исследования слабых оптических неоднородностей. Очень интересен также аспект применения переходных решеток для исследования релаксационных и спектроскопических характеристик атомных переходов (величины дипольных моментов, времена поперечной и продольной релаксаций, слабые расщепления уровней и т.п.) с целью установления фундаментальных закономерностей взаимодействия когерентного излучения с веществом.

Л и т е р а т у р а

1. Е.И.Штырков, В.В.Самарцев. Резонансная динамическая голография и оптическое сверхизлучение. В книге "Электромагнитное сверхизлучение", стр.398-426, Татполиграф, Казань, 1975.

2. Mc'Call S.L., E.L.Hahn. Phys. Rev. Lett., 18, 908, 1967; Phys.Rev., 185, 457, 1969.

3. C.L.Tang, H.Statz. Appl.Phys.Lett., 10, 145, 1968.

4. H.A.Kurnit, I.D.Abella, S.H.Hartman. Phys.Rev.Lеtt., 13, 567, 1964.

5. R.H.Dicke. Phyh.Rеv., 93, 99, 1954.

6. Е.И.Штырков. Оптика и спектроскопия, 45, стр.603, 1978.

7. Е.И.Штырков, B.C.Лобков, Н.Г.Ярмухаметов. Письма в ЖЭТФ, 27, стр.12, 685, 1978.

8. Л.Аллен, Дж.Эберли. Оптический резонанс и двухуровневые атомы, "Мир", М., 1978.

9. А.Абрагам. Ядерный магнетизм, ИЛ, М., 1963.

10. E.L.Hahn. Phys.Rеv., 80, 580, 1950.

11. C.V.Heer, Mc Manamon P.F., Opt.Соmmun., 23, N1, 49, 1977.

12. M.S.Shiron. Appl.Phys.Lett., 33, 4, 299, 1978.

13. Е.И.Штырков. Динамические голограммы на суперпозиционных состояниях атомов. В кн. "Голографические методы исследований", Л., стр.118-130, 1978.

14. E.I.Shtyrcov, N.L.Nevelskaia, V.S.Lobkov, N.G.Yarmukhametov. Phys.Stat. Solid (b), 98, 1980.

15. К.С.Мустафин, В.А.Селезнев, Б.И.Штырков. Авт.с.№ 272602 от 11.03.1968 г.; Опт. и спектр., 28, 6, 1186, 1970.

16. S.I.Shtyrkov, K.V.Samaratsev. Phys.Stat.Sol. (a), 45, 647, 1978.

17. J.Woldman. Opt.Соmm., 2, 212, 1970.