In the work "On the Electrodynamics of Moving Bodies" Albert Einstein pointed out that the extension of the relativity principle to optics and electrodynamics was assisted in part by "failed efforts to detect the motion of the Earth through the light-carrying medium". Einstein never specified, which particular experiences he meant. The appearance of the Special Theory of Relativity (STR) was considered by many physicists as an attempt to explain the null result of the Michelson-Morley experiment, in which the question of whether the Earth moves through the ether had been put in the most straightforward way. This belief has been implanted in the literature, particularly in the textbooks – it is quite convenient to deduce STR from the Michelson-Morley experiment.

As known, the purpose of the Michelson-Morley experiment was to measure the velocity of "ethereal winds" caused by movement of the Earth with respect to the ether – a hypothetical medium, filling, as thought by Michelson, all space and penetrating freely any substance and medium: solid bodies, liquids, and certainly gases. Let us take a look at an extent in which this opinion of Michelson corresponds to reality.

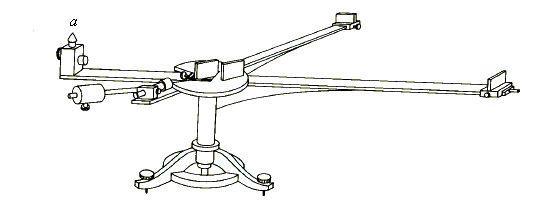
A general view of interferometer, as it was shown in Michelson’s report on the results of his experiment conducted in 1881, is given in Fig.1.

As described by Michelson, a source of light in his experiment was a small torch placed at a, followed by a lens so that the flame of the torch was in focus of the lens [1]. This torch is well seen on the figure. Due to the lens, the rays of light radiated by the torch become practically parallel.

In experiments of 1881, the interferometer was mounted on a metal cross-piece; in experiments of 1887 – on a massive concrete base, floating in a pool with mercury.

Fig.1

As well known, the Michelson-Morley experiment was aimed at detecting the speed of the "ether wind" produced by relative motion of the Earth through the ether – the hypothetical medium that fills all of space, as Michelson believed. A sketch of the Michelson-Morley experiment is displayed in Fig. 2. A monochromatic beam from a light source passes through a narrow slit in a screen A and through a lens that makes all light rays essentially parallel. The collimated light then falls onto a half-silvered mirror B, which is inclined at 45^o, whereupon the original beam is split into two coherent beams, one of which is reflected perpendicular to ether, while the other beam continues traveling parallel to this motion. At an equal distance L from the mirror B, two plane mirrors C and D are installed. Being reflected from these mirrors, the beams return back to mirror B, then they are partially reflected and partially transmitted by B, and finally get into the observing eyepiece E.

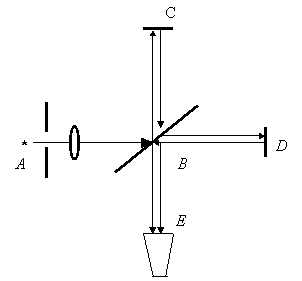
Fig.2

 It is known, that in carrying out the experiment, Michelson assumed that the ether was absolutely at rest and was not dragged by the moving Earth. The dynamics of the beams in the apparatus may be considered in two different frames of reference – one is fixed to the ether (call it the “stationary frame”), and the other is fixed to a moving interferometer (call it the “moving frame”). Clearly, in both frames the final interference results should be identical.

Consider the beams’ paths in the stationary frame, relative to which the apparatus moves with velocity v. According to the ether hypothesis, in this frame the speed of light is c. First look at the beam that travels from the half-silvered mirror B to the reflecting mirror D and back, shown in Fig. 3.

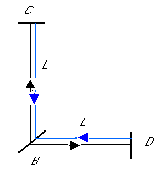
Fig.3

When the apparatus is at rest in the stationary frame, the time duration for the beam to travel from the mirror B to D and back is just T = 2L/c.

Suppose now that the apparatus moves through the ether in the direction shown by an arrow in Fig.4 with a speed v.

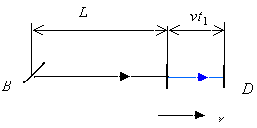
Fig.4

During the time t₁ that it takes the beam to travel along the path L, the mirror D shifts a distance vt₁. Then, the distance that the beam travels until it encounters the mirror D is equal to ct₁ = L + vt₁, whence it follows that

t₁ = L / (c + v).

On its way back from the mirror D the beam travels towards the mirror B, as shown in Fig. 5.

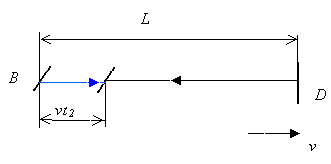
Fig.5

Before the beam encounters the mirror B, it covers distance ct₂ = L – vt₂, which yields t₂ = L / (c + v). Thus, the time required for the beam to travel from B to D and back in the stationary frame is equal to

By dividing both parts by c², we obtain:

In the moving frame, i.e. in the frame that is fixed to the traveling apparatus, the ether appears to move towards the apparatus in the direction opposite to the actual motion of the device. According to the pre-relativistic concepts, the speed of light is therefore equal to c–v as the beam travels from B to D, and c+ v on its way back, whence it follows that

t₁ = L / (c + v),

t₂ = L / (c + v),

T _|| = (2L / c) / (1 – v² / c²).

Thus, in both reference frames we obtain identical results for T _||.

Consider now the dynamics of the beam that travels at the right angle to the previous beam, and goes from mirror B to mirror C. In the frame moving together with the device, the ether moves in the direction opposite to the actual motion of the device, hence the beam deviates in the direction, where the “ethereal wind” blows and arrives to the point C’, which stands apart from the point C at a distance vt, as shown in Fig. 6.

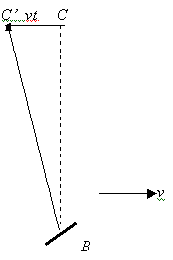
Fig.6

The speed of light for the beam that travels in the ВC’ direction, as measured in the frame fixed to a moving apparatus, appears to be , according to the ether hypothesis. During the time t the beam covers the distance . Since t = , we obtain t = L/c, and hence

T^ = 2t = 2L/c.

Consider now the dynamics of the beam in the stationary frame, which is fixed to the ether. Assume a wave front of the beam starts its way at an instant when the half-silvered mirror is at the point B. After time t, required for the beam to cover the path L, the mirror C shifts on a distance vt in the direction of the apparatus motion, and consequently the beam will get into the point C’ separated from the point C by the distance vt, and located on the side opposite to the direction of the apparatus motion, see Fig. 7.

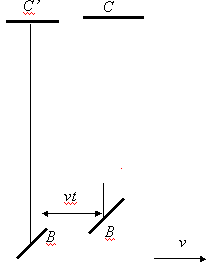
Fig.7

Then the path L from the point B (where the beam starts) to the point C’ is covered by the beam in time t = L / c, and the total path 2L is covered in

T^ = 2t = 2L/c.

Thus, in both frames of references we have the same result for T^ . It is important to stress the following: if the movement of the interferometer relative to ether really takes place, the perpendicular beam of light deviates in a direction, opposite to the actual movement of the interferometer, on distance CC ' = vL / c. Accepting v = 30 km/s and L = 11 m = 11000 mm, as it was in experiment of 1887, we obtain:

30 × 11000 / 300000 = 1.1 mm.

Actually, however, no deflection of the perpendicular beam was observed: the perpendicular beam arrives into the same point on the reflector as it would if the movement relative to the ether were absent.

In the moving reference frame, the arrival of the perpendicular beam back into the point C means, obviously, the absence of movement of the ether rather than interferometer. In such a case T^ is equal to 2L/c. Since in such experiment T| | is equal to T^ , then T| | = 2L/c. Thus, for an explanation of null result of Michelson-Morley experiment the hypothesis of Lorenz about the length contraction of the parallel arm of interferometer appears absolutely unnecessary!

However, Michelson was considering a course of beams in interferometer from the point of view of the observer stationary with respect to the ether, which is a surprising fact by itself, since both interferometer and Michelson are in the reference frame that moves relative to ether. So how does the motion of beams look like, in opinion of Michelson, from the point of view of the stationary observer? Here is, for example, the explanation of the Nobel Prize winner in physics R. Feynman [2]:

“... During time period t₃ the mirror C shifts to the right at a distance ut₃ (up to position C’), and the beam will travel along the hypotenuse ВС’ at a distance ct₃ (Fig. 8).

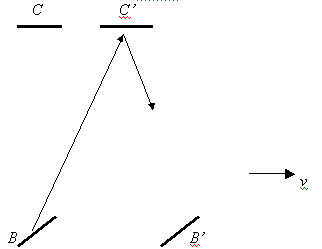
Fig.8

From a right-angle triangle it follows that (ct₃)² = L² + (ut₃)², or L² = (c t₃)² – (u t₃)² = (c² – u²) (t₃)², whence t₃ = L /. On the way back from a point C’ the beam has to travel the same distance; this follows from the symmetry of the path. So, the return time is the same (t₃), and the total time is equal to 2t₃. We write it down as 2t₃ = 2L / = 2(L/c)/”.

Using the designations used above, we rewrite this formula as

T^ = (2L/c)/.

The question that arises now is: Why does the beam have to deviate and follow the mirror C?

Michelson explains the deflection of the perpendicular beam like this [1]:

“The ray sa is reflected along ab (Fig. 9); the angle bab₁ being equal to the aberration angle; the beam then returns along ba₁ (aba₁ = 2), and goes to the focus of the telescope, whose direction is unaltered”.

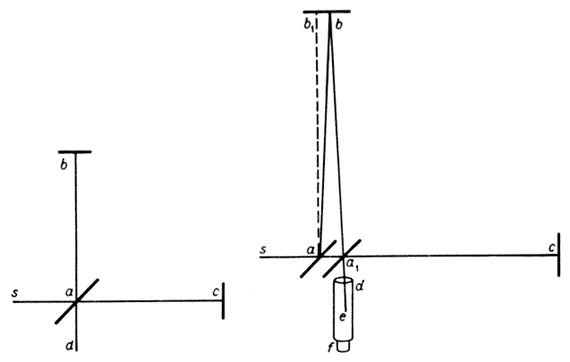
Fig.9

It is known, however, that aberration arises in case of movement of the detector of light relative to the light source. But in Michelson-Morley experiment the detector of light is stationary relative to the source during experiment. Thus, the deflection of the perpendicular beam following displacement of interferometer cannot be explained by aberration. So why, in such case, the perpendicular beam deviates following the displacement of interferometer, which moves, as we remind, with respect to the stationary observer?

Let us assume for a start, that a supersonic plane is flying strictly along the meridian of the Earth with a speed u, for example. How does the trajectory of this plane look like from the point of view of the observer stationary with respect to the Sun? Same as in the moving frame, the plane flies strictly along the meridian, but the meridian itself moves perpendicular to the plane motion at the orbital speed of the Earth v. In such a case, according to the Galileo-Newton laws of mechanics, the trajectory of the plane is a hypotenuse of a right-angle triangle with sides u and v, as shown in Fig.10:

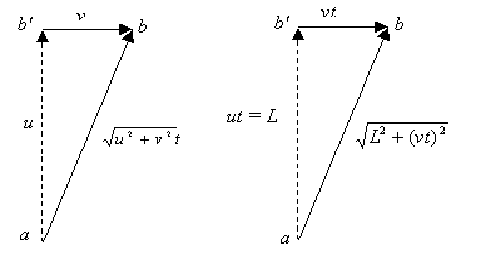
Triangle of velocities Triangle of distances

Fig.10

After time t, during which the plane in the moving frame travels a distance L between two points that are on the meridian in the stationary frame, the plane on the other hand travels a distance ab = in the stationary frame. As seen from the triangle of distances, the path ab in the stationary frame is equal to , so that

=

Thus, the time, during which the plane covers the distance L between points a and b, laying on the meridian, appears identical and equal t = L / u in both moving and stationary frames.

Let's assume further, that strictly along the meridian, the linear accelerator of elementary particles is laid, in which particles move with some speed u. Similar to the previous case, particles travel strictly along the accelerator; in stationary frame the accelerator is displaced with orbital velocity perpendicular to direction of particles’ motion. And in this case, too, as shown above, the trajectory of particles is a hypotenuse of a right-angle triangle with the sides u and v, as shown in Fig.10.

After time t, during which the particle in the moving frame travels a distance L in the accelerator, the same particle in the stationary frame covers a path ab =. From triangle of distances, the path ab in the stationary frame is equal to , so that

Thus, the time, during which the particle covers distance L in the accelerator, appears identical and equal t = L / u in both moving and stationary frames.

Let's assume now that strictly along the meridian, a glass rod of length L is laid, in which the pulses of light move at speed u, as it was in Shamir and Fox experiment [3]. In both moving and stationary frames the pulses move strictly along the glass rod; however, the glass rod is displaced with orbital speed perpendicular to direction of the pulses’ motion.

And in this case, too, as shown above, the trajectory of each pulse of light is a hypotenuse of a right-angle triangle with the sides u and v, see Fig.10. After time t, during which the pulse of light in the moving frame travels a distance L, the same pulse in the stationary frame covers a path ab = . From triangle of distances, the path ab in the stationary frame is equal to , so that

Thus, the time, during which the pulse of light covers distance L in the rod, appears identical and equal

t = L / u in both moving and stationary frames.

Let's assume, at last, that the beam of light travels in air with speed c strictly along the meridian, as it was in Michelson-Morley experiment. As the results of experiment have shown, in the moving frame the perpendicular beam travels strictly between points a and b, one of which (a) lays on a half-transparent mirror, and another (b) – on the reflecting mirror. Obviously, the perpendicular beam of light should travel between the same two points a and b in the stationary frame as well. Thus, the following situation is observed: the perpendicular beam of light travels along the line between two points a and b, however this line is displaced, from the point of view of the stationary observer, at the speed of orbital motion of the Earth. Then, if the perpendicular beam actually deviates in a direction of orbital motion of the Earth – and so it did actually – then the reason of such deflection, similar to all cases considered above, is the velocity addition of the motion of the perpendicular beam and the orbital motion of the Earth. In such a case, according to the Galileo-Newton laws of mechanics, the trajectory of the perpendicular beam of light is a hypotenuse of a right-angle triangle with the sides u and v, as seen from Fig.10 (in our case, u = c). Then, after time t, during which the perpendicular beam in the moving frame travels a distance L between points a and b, in the stationary frame the same beam covers path ab, equal to . From the triangle of distances, the length of the path ab in the stationary frame is equal to , so that

In the moving frame, obviously, the time is t = L / с. Thus, the time, during which the beam of light travels the distance L, appears identical and equal t = L / c in both moving and stationary frames.

In Shamir and Fox experiment, the deflection of perpendicular beam is actually caused by addition of velocity of the beam and velocity of moving medium – the glass rod, where the beam propagates. But then it means, contrary to common opinion, that the ether within the glass rod is completely, rather than partially – Fresnel like, dragged by the rod. In other words, the ether that is trapped between the molecules of glass, together with these molecules represent a continuous optical medium that travels with respect to any other reference frame as a whole entity.

Exactly the same, in the Michelson-Morley experiment the deflection of the perpendicular beam is actually caused by addition of velocity of beam and velocity of moving medium – air of the Earth, in which the beam in this case propagates. It means that, contrary to common opinion, the ether within the atmosphere of the Earth is completely, rather than partially as thought by Fresnel, dragged by the air. In other words, the ether that is trapped between molecules of gases that constitute atmosphere, together with the molecules represent a continuous optical medium that travels with respect to any other reference frame as a whole entity.

Thus, the discussion above leads to conclusions:

1. The deflection of the perpendicular beam following the displacement of interferometer observed in the stationary frame is caused by addition of velocity of the perpendicular beam and the velocity of atmosphere that travels at the orbital speed of the Earth.
2. The null result of the Michelson-Morley experiment is caused by absence of motion of the interferometer with respect to the medium where the beams of light propagate, i.e. the Earth’s atmosphere; this is the only correct and non-contradictory explanation of the null result of the given experiment. Hence, despite of the null result, the Michelson-Morley experiment is not a confirmation, but on the contrary, a disproof of the Theory of Relativity of Lorenz and Special Theory of Relativity of Einstein.
3. Since there was no motion of interferometer with respect to the medium where the light propagated in both the Michelson-Morley experiment and Shamir and Fox experiment, the time T^ is equal to T| | = 2L/c. Thus, for an explanation of null result of the Michelson-Morley experiment, the hypothesis of Lorenz about length contraction of the parallel arm of interferometer turns out to be unnecessary.

At the same time, "the vortex experiment" of Sagnac proves that in case when interferometer travels with respect to the medium where the light propagates, the interference pattern does change, in accord with the speed of interferometer relative to a "light-carrying medium"; the result does not depend on whether this medium is air, or vacuum, or the ether. Thus, the null result of Michelson-Morley experiment is not the proof of impossibility to detect any effects caused by movement of the observer relative to the ether. All that the Michelson-Morley experiment proves, as well as many other experiments, is the absence of the ether’s motion in the Earth’s atmosphere – nothing else!

1. Albert A. Michelson, Edward W. Morley. On the Relative Motion of the Earth and the Luminiferous Ether. The American Journal of Science. III series. Vol. XXII, No. 128, P.120 – 129.
2. P. Feynman, P. Leigton, M. Sands/ The Feynman lectures of Physics. Addison –Wesley publishing company, inc., Reading, Massachusetts, Paolo-Alto. London, 1963.
3. У.И.Франкфурт. Оптика движущихся сред и специальная теория относительности. Эйнштейновский сборник 1977, Москва, Наука, 1980 (in Russian).
4. Shamir J., Fox R. A new experimental test of special relativity. Nuov. Cim., 1969, 62B, p.258-264.