Экспериментальные нарушения принципов относительности, эквивалентности и сохранения энергии
Стефан МАРИНОВ
Институт Фундаментальной Физики
Морeлленфельдгассе 16, А-8010 Грац, Австрия
Теперь можно рассмотреть несколько экспериментов, осуществленных мною, которые легитимируют абсолютную пространственно-временную теорию и выбрасывают за борт всю теорию Эйнштейна.
ОПТИЧЕСКИЕ ИЗМЕРЕНИЯ АБСОЛЮТНОЙ СКОРОСТИ ЗЕМЛИ
Во всех экспериментах по измерению световой скорости измеряется сумма скоростей света на определенном участке пути "туда и обратно", так что если скорость света "туда” больше на величину скорости лаборатории и "обратно" на ту же величину меньше, то средняя скорость, которая на самом деле при таком эксперименте измеряется, остается величиной постоянной.

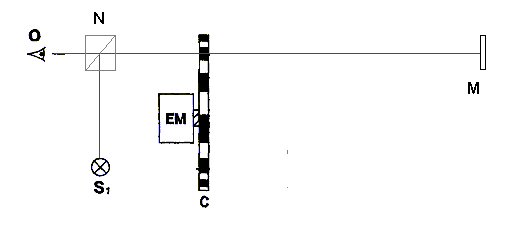
На рис.1 показана схема подобного эксперимента. Свет от источника S, проходя через полупрозрачное зеркало N, "нарезается" на куски вращающимся зубчатым колесом С, покрывает расстояние d до зеркала М, возвращается обратно, снова проходит через прорези вращающегося колеса С и, отражаясь от полупрозрачного зеркала N, доходит до наблюдателя О. Если за время прохождения пути d туда и обратно колесо поворачивается с прорези на, зуб, то наблюдатель света видеть не будет. Разделив расстояние 2d на время, за которое колесо поворачивается с прорези на зуб, получаем скорость света.
Такой эксперимент впервые провел Физо в 1849-ом году. Сегодня люди проводят сотни тысяч подобных измерений за день, так как на Земле функционируют сотни тысяч радаров. Однако, никто (повторяю, никто, никто, никто) не постарался измерить скорость света в одном направлении, хотя такой эксперимент предложили еще Майкельсон и Морли в их известной статье 1881 года, где они сообщают о нулевом результате, полученном при попытке определения абсолютной скорости Земли с помощью Майкельсонова интерферометра.
Суть подобного эксперимента настолько проста, что даже ребенок, разобравшись в эксперименте Физо, может его предложить. Однако, как это ни странно, никто в мире не взялся такой эксперимент поставить, тем более что технических трудностей не так уж много.
На рнс.2 показана схема эксперимента, при помощи которого я измерил разность световых скоростей в двух противоположных направлениях [5, стр.68]. Свет от лазера разделяется полупрозрачным зеркалом на два пучка, которые, отражаясь от еще пары зеркал, проходят в противоположных направлениях расстояние между двумя синхронно вращающимися дисками с дырами по периферии (на рисунке источники света S1 и S2 показаны как независимые). Первым вращающимся диском свет нарезается на куски. Второй вращающийся диск пропускает большую часть куска, если скорость света в этом направлении большая, соответственно, меньшую часть куска, если скорость света в этом направлении меньшая.
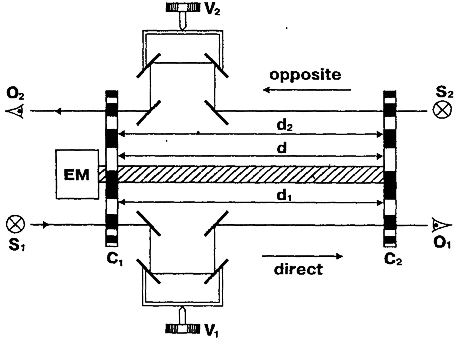
Рис.2. Эксперимент со связанными затворами для измерения скорости света в одном направлении.
Так как расстояние между дисками нельзя сделать очень большим (Физо работал при базисном расстоянии d=8 км), то световые куски, движущиеся с большей скоростью, проходят через второй диск только чуть-чуть длиннее, чем куски, движущиеся в обратном направлении
с меньшей скоростью. Однако, если за "вторым" диском поставить, чувствительные фотодиоды, то из разности генерируемых ими токов, измеряемой на гальванометре, можно определить проекцию абсолютной скорости лаборатории по направлению оси аппарата. Я назвал этот эксперимент "экспериментом со связанными затворами" (coupled shutters experiment). Вот вся его теория и исполнение:Вал вращается электромотором, поставленным в середине вала (на рис.2 мотор поставлен в левом конце вала). Расстояние между центрами периферийных дыр и оси вала
R (12 см), а расстояние между дисками d (120 см). Взаимное положение обоих дисков на валу и направление лазерных пучков устанавливаются так, что когда вал в покое, световой пучок, проходящий целиком через ближнюю дыру, освещает половину дальней дыры. Так как при вращении световым импульсам, нарезанным ближней дырой, нужно известное время, чтобы достичь дальней дыры, с увеличением скорости вращения все меньше и меньше света пройдет через дальнюю дыру, если она "убегает" от пучка и, наоборот, все больше и больше света пройдет через дальнюю дыру, если она "прибегает" к пучку. Для краткости, дыры в первой позиции я называю "убегающими" н дыры во второй позиции "прибегающими".Допустим, что дыры на вращающихся дисках прямоугольные и что лазерные пучки имеют прямоугольное сечение и равномерную освещенность в сечении (эти ограничения, облегчающие нам вычисления, не влияют на вид окончательной формулы). Ток
I, генерируемый каждым из фотодетекторов, будет пропорционален ширине светового пятна на его поверхности, b, когда вал вращается, т.е. I ~ b. Когда скорость вращения возрастает на ΔN об/сек, ширина светового пятна за "убегающей" дырой станет b-Δb, тогда как ширина светового пятна за "прибегающей" дырой станет b + Δb, и соответствующие токи будут равны I - ΔI ~ b - Δb, I + ΔI ~ b + Δb, так, чтогде dI - половина измерения разности токов, производимых обоими фотодетекторами в этом случае.
Если вращать вал сначала с ΔN/2 об/с в одну сторону, а потом с ΔN/2 об/с в другую сторону, то это соответствует изменению угловой скорости на ΔN. Так как
мы получим для скорости света в одном направлении
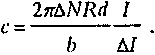 (44)
(44)Если скорость света в одну сторону c-v, а в другую c+v, то изменения токов будут соответственно, dI + δI и ΔI - δI, и мы будем иметь
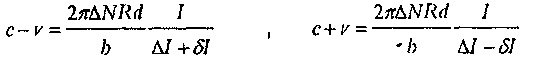 (45)
(45)Из этих двух уравнений получаем окончательный результат:
Метод измерения токов ΔI и δI состоит в следующем. Изменяется скорость вращения вала на dN (400 об/с) и измеряется изменение тока ΔI ~ ΔI +- δI, производимого каждым из фотодетекторов.
Потом измеряется разность 2δI этих двух изменений токов. Я провел оба измерения дифференциальным методом, пропуская через гальванометр разность токов, генерируемых обоими фотодетекторами. Чтобы измерить 2ΔI, я ставил диски так, чтобы дальние дыры для одного светового пучка были "убегающими", а для другого "прибегающими". Чтобы измерить 2δI я ставил диски так, чтобы дальние дыры для обоих пучков были либо "убегающими", либо "прибегающими".
Измерение разности токов 2ΔI делалось однократно и я получил 2ΔI=105 мкА.
Измерение разности токов 2δI я проводил с 9-го по 13-е февраля 1984 г. в Граце (φ =47°, λ=15°26'), делая замеры круглосуточно каждые два четных часа. Так как я делал эксперимент один, некоторые часы в некоторых днях пропускались. Ось аппарата была поставлена по направлению "север-юг", и на полученном за эти пять дней квази-синусондальном графике я отметил две максимальных разности токов (2δI)а=-120 нА и (2δI)b=50 нА в соответствующих стандартных часах времени, tst, которые (вместе с оцененными мною вероятными погрешностями) соответствовали двум максимальным за сутки проекциям абсолютной скорости Земли по оси аппарата
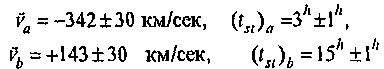 (47)
(47)Когда 2δI имеет экстремальное значение, абсолютная скорость Земли лежит в плоскости лабораторного меридиана (рис.З). Компоненты скорости, направленные на север, принимаются положительными, а компоненты скорости, направленные на юг - отрицательными. Я отмечал через va ту компоненту скорости, чья алгебраическая величина меньше. Когда оба пучка света проходят через "убегающие" дыры, тогда, в случае, что компонента абсолютной скорости направлена на север, "северный" фотодиод производит меньше тока, чем "южный" фотодиод (по отношению к случаю, когда компонента абсолютной скорости перпендикулярна к оси аппарата). Нужно отметить, что на рис.3 обе компоненты скорости направлены на север и положительны, но в действительности компонента va была отрицательна.
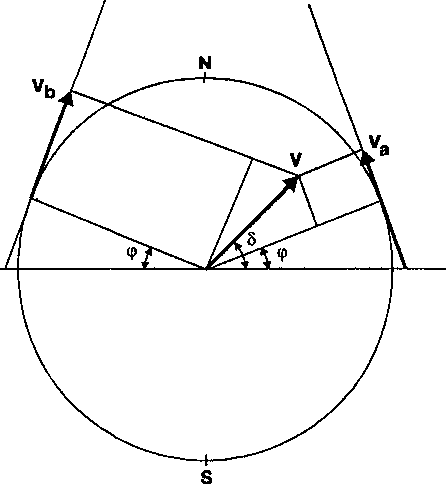 Рис.3. Абсолютная скорость Земли и ее компоненты в горизонтальной плоскости в момент, когда абсолютная скорость параллельна меридианной плоскости.
Рис.3. Абсолютная скорость Земли и ее компоненты в горизонтальной плоскости в момент, когда абсолютная скорость параллельна меридианной плоскости.Как видно из рисунка 3 обе компоненты абсолютной скорости Земли в горизонтальной плоскости лаборатории, va и vb связаны с модулем абсолютной скорости v следующими зависимостями:
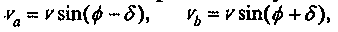 (48)
(48)
где ф - географическая широта лаборатории, а δ - склонение апекса абсолютной скорости. Из этих формул получаем:
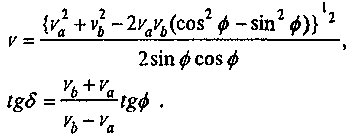 (49)
(49)
Очевидно апекс абсолютной сорости v направлен к меридиану va. Следовательно прямое восхождение апекса равняется местному звездному времени регистрации va. Так как точность определения момента регистрации va была +-1h, то было достаточно вычислить (с точностью не выше +-5 мин) звездное время tsi для меридиана, где местное время то же, что и стандартное время регистрации, принимая во внимание, что звездное время в среднюю полуночь следующее:
| 22 сентября - 0h | 23 марта - 12h |
| 22 октября - 2h | 23 апреля - 14h |
| 22 ноября - 4h | 23 мая - 16h |
| 22 декабря - 6h | 22 июня - 18h |
| 21 января - 8h | 23 июля - 20h |
| 21 февраля - 10h | 22 августа - 22h |
Местное звездное время регистрации va (т.е. прямое восхождение апекса абсолютной скорости) было вычислено следующим способом, так как за день звездное время возрастает на 4 минуты (по отношению к солнечному времени), звездное время в полночь 11 февраля (день, являющийся средним в серии моих измерений, который следует через 21 день после полуночи 21-го января) было 8h+1h24m = 9h24m. В 3h средне-европейского времени (то есть стандартного времени Граца) 11 февраля местное звездное время на 15° меридиане было 9h24m+3h= 12h24m. На меридиане Граца звездное время было 12h24m+2m=12h+26m≈l2,5h и это было прямое восхождение апекса абсолютной скорости. Подставляя теперь значения (47) в формулы (49), я получил для модуля абсолютной скорости Земли и для экваториальных координат ее апекса
v = 362 ± 40 км/сек , δ = -24° ±7°, а = (tst)a = 12,5h ± Ih (50)
Отмечу в конце (см. рис.2), что эксперимент со связанными затворами можно проделать при помощи микрометрических винтов V1 и V2, изменяющих длины путей световых импульсов между дисками, используя гальванометр, измеряющий разность токов, генерируемых фотодетекторами, только как нулевой инструмент. Легко видеть, что если при данном положении аппарата установим нулевой ток в гальванометре, когда длины путей световых импульсов равны соответственно d1 = d+a, d2 =d+a, где а - удлинение путей из-за отклонений, то если повернем ось аппарата на 180°, чтобы ток остался нулевым, нужно будет изменить длины путей световых импульсов на
d1́ = d(l-2v/c)+a,
d2΄=d(l+2v/c)+a
(в случае, если проекция абсолютной скорости лаборатории по оси аппарата, v, направлена слева направо на рис.2) или же одним из микрометрических винтов изменить длину одного из путей на
Δd = d΄
2 - d΄1 = 4(v/c)d. (51)Для v = 300 км/сек и d = 120
см будем иметь Δd = 4,8 мм.В 1973 г. в Софии я проделал "девиационный эксперимент со связанными зеркалами" [10]. Он был не очень точен и я измерил только максимальную проекцию абсолютной скорости Земли по оси аппарата (чей азимут был 84°), получив величину v = 130± 100 км/сек.
В 1975/76 г.г. в Софии я проделал "интерференционный эксперимент со связанными зеркалами [11], который был гораздо точнее. Проводя измерения в течение шести месяцев, я получил для модуля абсолютной скорости Солнца v=303±20 км/сек и для экваториальных координат ее апекса 8=-23°±4°, α
= 13h23m±20mЛИТЕРАТУРА
[1] Marinov S. Eppur si muove (East-West, Graz, 1987), first ed. 1977
[2] Marinov S. Classical Physics (East-West, Graz, 1981).
[3] Marinov S. Divine Electromagnetism (East-West, Graz, 1993)
[4] Marinov S. The Thorny Way of Truth, part IV (East-West, Graz, 1989)
[5]. Marinov S. The Thorny Way ot'Truth, part II (East-West, Graz, 1986)
[6] Marinov S. The Thorny Way ot'Truth, part VII (East-West, Graz, 1990)
[7] Marinov S. Nature 322, p. x (21 August 1986)
[8] Marinov S. New Scientist 112, 48 (1986)
[9] Rindler W.American Journal ot'Physics 57, 993 (1989)
[10] Marinov S. Czechoslovak Journal of Physics B24,965 (1974)
[11] Marinov S. General Relativity and Gravitation 12, 57 (1980)
[12] Marinov S. Indian Journal of Theoretical Physics 31,93 (1983)
[13] Kennard R. Philosophical Magazine 33,179 (1917)
[14] van Bladel J. Relativity and Engineering (Springer, Berlin, 1984)
[15] Marinov S. The Thorny Way ot'Truth, part I (East-West, Graz, 1988), first ed. 1982.
[16] Scott W.T. The Physics of Electricity and Magnetism (John Wiley, New York, 1966)
[17] Dasgupta B.B. American Journal ot'Physics 52, 258, (1984)
[18] Rowland H.A. Sitzungsberichte der k. Akademic der Wissenschaften zu Berlin, p.211 (1876)
[19] Ландау Л.Д. и Лифшиц Е.М. Электродинамика сплошных сред (изд. "Наука", Москва, 1973)
[20] Marinov S. Deutsche Physik 3(12), 53 (1994)
[21] Marinov S. Deutsche Physik 4(13), 31 (1995)
[22] Marinov S. Deutsche Physik 3(9), 17 (1994)
[23] Marinov S. Deutsche Physik 3(10), 8 (1994)
[24] Marinov S. Deutsche Physik 3(11), 40 (1994)
[25] Marinov S. Deutsche Physik 3(12), 13 (1994)
[26] Marinov S. Deutsche Physik 4(13), 15(1995)