(Received 21 May 1999; accepted 13 September 1999)

Abstract. Partitions of 178.8-year intervals between instances of retrograde motion in the Sun's oscillation about the center of mass of the solar system seem to provide synchronization points for the timing of minima and maxima in the 11 -year sunspot cycle. In the investigated period 1632-1990, the statistical significance of the relationship goes beyond the level P = 0.001. The extrapolation of the observed pattern points to sunspot maxima around 2000.6 and 2011.8. If a further connection with long-range variations in sunspot intensity proves reliable, four to five weak sunspot cycles (R < 80) are to be expected after cycle 23 with medium strength (R ~ 100).

Since the discovery of the 11 -year sunspot cycle by Schwabe in 1843 astronomers and astrophysicists have tried to explain how this fundamental cycle and its complex magnetic features come into existence. The switch of polarity in sunspot dipoles around the sunspot minimum shows that the 11 -year cycle is actually half of a 22-year magnetic cycle (Hale cycle), during which the polarity of sunspot groups reverses twice, hence returning to its original magnetic state. Babcock's dynamo model relates the dynamics of the 22-year magnetic cycle to the Sun's rotation on its axis. The interaction of differential rotation, the polar magnetic field, and convection in the solar plasma is thought to cause dynamo action that generates the sunspot cycle by magnetic field amplification. So it should be expected that variations in the Sun's rotation rate are reflected in the level of sunspot activity. Accordingly, Clark et al. (1979) showed that in 1957, when the sunspot activity was nearly three times more intense than in 1884, the rotation in the sunspot zone took half a day longer than in 1884.

Yet the Sun's spin momentum, related to its rotation on its axis, is only one component of its total angular momentum. The other factor is the Sun's orbital angular momentum linked to its irregular oscillation about the center of mass of the solar system. The contribution of the orbital momentum to the total angular momentum is not negligible. The maximum value reaches 25% of the Sun's spin momentum. In addition, there is strong variation. The orbital angular momentum varies from —0.1 x 10⁴⁷ to 4.3 x 10⁴⁷ g cm² s¹ or reversely, which is more than a forty-fold increase or decrease. If there were transfer of angular momentum from the Sun's orbit to the spin on its axis, this could make a difference of more than 5% in its equatorial rotational velocity (Blizard, 1982). Such acceleration or deceleration has been actually observed (Landscheidt, 1976). This seems to be indicative of a case of spin-orbit coupling of the spinning Sun and the Sun revolving about the center of mass involving transfer of angular momentum (Landscheidt, 1986b, 1988). Coupling could result from the Sun's motion through its own ejected plasma. The low corona can act as a brake on the Sun's surface (Dicke, 1964).

So it seems reasonable to investigate whether there is a relationship between the Sun's irregular motion about the center of mass and the sunspot cycle. Jose (1965), who performed the first computer analysis of the Sun's motion, discovered a cycle of 178.8 years that he also found in sunspots. He tried a forecast of extrema in the 11 -year sunspot cycle based on the observed parallel course of the rate of change of the orbital angular momentum about the instantaneous center of curvature and the 22-year magnetic sunspot cycle. His prediction covered four minima and maxima between 1963 and 2009. From 1990 on the deviation of the observed extrema from the predicted time reached 3 to 8 years. Other studies of different aspects of the Sun's motion (Arriaga, 1955; Wood and Wood, 1965; Pimm and Bjorn, 1969; Landscheidt, 1976, 1983, 1986a,b, 1988, 1990; Blizard, 1982, 1987; Fairbridge and Sanders, 1987; Fairbridge and Shirley, 1987) did not continue Jose's endeavor to find close connections with extrema in the magnetic sunspot cycle .

Jose (1965) did not relate the 178.8-year cycle to special events in the Sun's motion. He only observed that the Sun's path about the center of mass and functions like the rate of change in the orbital angular momentum form patterns that repeat at intervals of 178.8 years. Yet there are special events in the Sun's motion that constitute a 178.8-year repeat pattern. Jose was the first to point at these phenomena. Around 1632, 1811, and 1990 the Sun's motion relative to the center of mass was retrograde and the orbital angular momentum, which had been positive for centuries, became negative. The next retrograde Sun event (RSE) will occur around 2169. If there is a relationship between the Sun's motion and solar activity, the intervals of 178.8 years between RSEs might provide synchronization points for the magnetic sunspot cycle, especially as Jose has shown that there is a cycle of 178.8 years in sunspot activity.

There is circumstantial evidence that RSEs actually release instability in the solar plasma. The recent change in the Sun's orbital angular momentum from positive to negative values occurred in September 1989. Just around this time, from August to October 1989, energetic solar eruptions emitted the most intense solar cosmic rays measured since the beginning of the Space Age. One of these flares, observed 19 October 1989, produced more cosmic rays than the previous solar cycle in total (Siscoe, 1991). The count of energetic particles reached 40000 particle flux units (p.f.u.) at energies above 10 MeV. Had there been an astronaut on the moon, wearing only a space suit, death would have been probable?

The relativistic solar particle events in September and October 1989 were characterized by very unusual time profiles not seen since the beginning of the observation of solar cosmic rays in 1942. Contrasting sharply with the typical smooth rise and fall, they displayed bumpy profiles richly structured in a manner that was strikingly different from station to station. Even more extraordinary was a sharp spike observed after the 19 October event. Moreover, nearly all of the RSE-related solar cosmic ray events originated with southern hemisphere flares, whereas the other parent flares observed since 1942 had concentrated on the northern hemisphere (Bieber, Evenson, and Pomerantz, 1990). A few months before the reversal of sign of the Sun's orbital angular momentum, there was already a barrage of very energetic X-ray flares and proton events that resulted in a great magnetic storm on 13 March 1989 which had the most disturbed 24-hour period of any recorded since the beginning of dependable observations in the 1860s. Mayaud's geomagnetic aa index reached the value 450. The strongest geomagnetic storm falling at the highly active sunspot cycle No. 19, observed 15 July 1959, only reached the aa value 357. Through 1990 there were no outstanding eruptions on the Sun. This changed again, when the Sun's orbital angular momentum returned to positive values in January 1991. A barrage of energetic events began just at this time and ended in June 1991. A proton flare observed 23 March 1991 was even more spectacular than the energetic event in October 1989. It reached the flux level of 43 000 p.f.u.. Taken together, these observations show that at least solar eruptions occurring around the RSE 1990 reached exceptional levels of energy display and were qualitatively different from eruptions observed in other periods.

There is no way to check the Sun's eruptional activity at the time of earlier RSEs directly. Regular flare observations were not possible before the invention of the Lyot filter in 1933, and the first observation of a solar flare in white light was made by Carrington and Hodgson in 1859. The strength of the solar wind, partly driven by solar eruptions, is indirectly indicated by radiocarbon data. Yet ¹⁴C age is plagued by errors (Stuiver and Polach, 1977) which hinder a precise assessment necessary for the evaluation of flare activity within a relatively short interval. It has been shown, however, that there is a close connection between variations in the Sun's positive orbital angular momentum and solar activity. As positive momentum is the prevailing condition for centuries, it may be expected that a switch to negative momentum has a disturbing effect which also affects the Sun's activity, though perhaps in a different way.

According to Pimm and Bjorn (1969), 49% of the variance in sunspot number can be related to the Sun's positive orbital angular momentum and the curvature of its path around the barycenter. This is based on a correlation coefficient r = 0.7. Further 9.8% of the sunspot variance can be explained by Sun-centered Coriolis acceleration (Blizard, 1987). I showed in the early eighties that there is a secular cycle in the time rate of change of the Sun's orbital angular momentum that is in phase with the secular Gleissberg cycle which modulates the amplitudes of the 11-year sunspot cycle. Since A.D. 300, the solar motion cycle has correctly indicated all maxima and minima in the Gleissberg cycle, though the length of this cycle varies from 40 to 120 years. An evaluation of this connection by a /²-test yields highly significant results far beyond the level P = 0.001 (Landscheidt, 1986a, 1987). The secular solar motion cycle points to waning sunspot activity past 1990 and a deep sunspot minimum around 2030. Forecasts in 1984 (Landscheidt, 1986a, 1987), based on these data, seem to be in accordance with the actual development after 1990. Though a panel of experts on solar cycle forecast (Joselyn et al, 1997) predicted in 1996 and even two years later that cycle 23 would have a large amplitude similar to the preceding cycles (highest smoothed monthly sunspot number R = 160), the course of the data in the first three years of the cycle shows that a peak around R — 100 is more realistic. The Sunspot Index Data Center, Brussels, now expects a maximum at R = 97. Even more conspicuous is the weakness of eruptional activity in cycle 23.

A subcycle of the secular solar motion cycle makes it possible to predict solar eruptions. My long-range forecasts of precisely denned classes of energetic X-ray flares and strong geomagnetic storms, covering the period 1979-1985, reached an overall hit rate of 90% though such events show a very irregular distribution. These forecasts were checked by the Space Environment Center, Boulder, and the astronomers Gleissberg, Wohl, and Pfleiderer (Landscheidt, 1986b; Landscheidt and Wohl, 1986). Accumulations of strong geomagnetic storms around 1982 and 1990 were also correctly forecast several years before the event (Landscheidt, 1988).

Another indication of the effects of change in the Sun's positive orbital angular momentum are unilateral accumulations of optical flares irrespective of the Sun's rotation on its axis. When centrifugal force is dominant in the Sun's motion, flares occur more frequently on the side far from the center of mass of the solar system (CM). Dominance of gravitation coincides with flare accumulations on the side pointing toward CM. This directional effect occurs only when the strength of impulses of the torque in the Sun's motion goes beyond a special quantitative threshold. Phases of weak change in the orbital angular momentum go along with evenly distributed flares. Statistical tests show that the result is significant at a level far beyond P = 0.001. After a strong positive impulse of the torque in 1951, for instance, out of 1318 flares observed in the years 1951 to 1956, as much as 886 occurred on the side away from CM and only 432 on the side pointing toward CM. A forecast of the flare distribution in 1983 and 1984 turned out correct (Landscheidt, 1986b, 1988).

In the light of these effects linked to change in the Sun's positive angular momentum and the observed coincidence of outstanding solar eruptions and reversals of the sign of momentum, it seems promising to see whether the 178.8-year intervals between consecutive RSEs (RSI) can be related to sunspots, though perhaps in a different way as with regular positive momentum. It attracts attention that half of the RSI - 89.4 years - falls within the range of the length of the Gleissberg cycle. It is also noticeable that the fourth part of the RSI - 44.7 years - has not only the length of the double Hale cycle, quoted in the literature (Schove, 1983), but also indicates periods of strong sunspot activity covering several decades. After 1700 the fourth parts of RSIs fell at 1766, 1856, and 1945. In each case, this was the start of a sequence of two to three strong 11-year cycles. In the case 1856 the strong activity additionally included two earlier cycles. The whole interval and its half and fourth parts point to the geometric progression 1, inversely related to powers of 2. This elementary progression plays a fundamental role in natural sciences and is also part of the Titius-Bode Law of planetary distances and von Weizsacker's nebular theory which explains the power 2 progression and its role in the formation of the distance pattern (Nieto, 1972).

Continued investigation along these lines shows that the 8th part and the 16th part of the RSI are closely connected with sunspots.The 8th part, equal to 22.35 years, is close to the mean length of the complete magnetic cycle of 22.1 years. The 16th part of the RSI, equal to 11.175 years, and the mean length of the 11-year sunspot cycle of 11.05 years, based on continuous observations available since 1700, are equally close to each other. This match disappears when a geometric progression is chosen that is based on powers of 3. Fairbridge and Hameed (1983) have shown that there is significant phase coherence of 11 -year sunspot minima in two consecutive 178-year intervals even if they are not related to special initial events. The minimum phases observed in the first interval show a repeat pattern in the second interval, though only a rough one. The level of significance is P = 0.02.

So I investigated the two RSIs delimited by RSEs 1632.6, 1811.4, and 1990.3 to see whether they are related to the shorter sunspot cycles. As the magnetic cycle is set apart from the 11-year cycle only by magnetic polarity that has no effect on sunspot numbers, I compared the distribution of the 16th parts in the two RSIs with the 11 -year sunspot minima and maxima falling in the period between 1632 and 1990. Historical yearly sunspot data were taken from Schove (1983) and Waldmeier (1961). Recent data were provided by the Sunspot Index Data Center, Brussels.

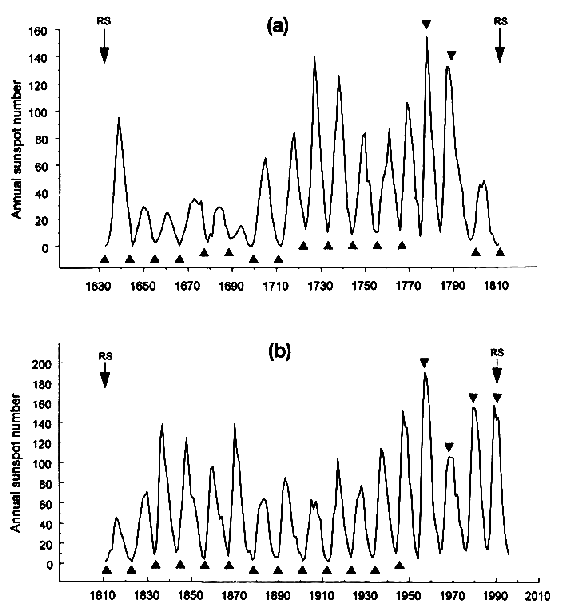
Figures l(a) and l(b) show the result for the respective RSIs. Initial phases of these intervals are indicated by arrows and the label RS. Sixteenth parts of RSIs (SP) are marked by filled triangles. Nearly all of the 33 SPs coincide within a relatively small range with sunspot extrema. In both of the RSIs investigated, the first 13 SPs go along with sunspot minima. A switch to maxima in the earlier RSI after the 13th SP is exactly repeated in the later RSI. Only after 15 conforming SPs there is a divergence including the last two SPs.

Figure 1. Distribution of 16th parts (filled triangles) of 178.8-year intervals between retrograde phases in the Sun's motion about the center of mass of the solar system (arrows) in relation to extrema of the 11-year sunspot cycle in the periods 1632-1810 (a) and 1811-1990 (b). The associations in both of the 178.8-year intervals show the same pattern with the exception of the last two extrema. Such divergence seems to balance the accumulating difference in length between 16th parts (11.175 years) and sunspot cycles (11.05 years). The extrapolation of the pattern, covering nearly 360 years, points to future sunspot maxima around 2000.6 and 2011.8.

In the first cycle the SPs fall back at minima, whereas in the second cycle the association with maxima continues. Such a divergent course was to be expected. The difference of 0.125 years between the mean length 11.05 years of the sunspot cycle and the length 11.175 years of SP is small, but accumulates over longer periods and must be balanced. Especially secular periods of weak sunspot activity with longer cycles as after 1790 or between 1880 and 1930 and of strong activity with shorter cycles as after 1940 make compensations necessary.

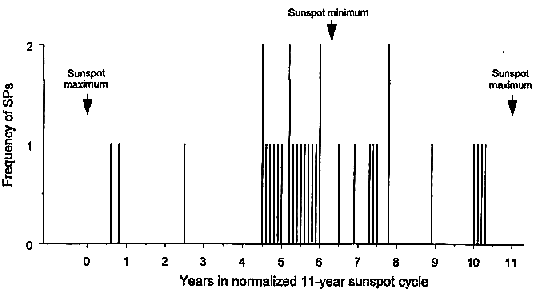
Figure 2. Frequency distribution of 16th parts of 178.8-year intervals from 1632 to 1990 within the
normalized 11-year sunspot cycle. The close association with sunspot minimum and maximum is
statistically significant beyond the level P = 0.001.

The association of a sunspot maximum with the recent RSE 1990 differs from the two preceding RSEs that were related to minima. This indicates that changes in the association are predominately linked to compensation processes, though there may be a basic association pattern that prevails as long as the differences between the length of sunspot cycles and SPs do not accumulate to such a degree that compensation becomes inevitable.

Two RSIs are not enough to decide what the basic association pattern looks like. The investigation is still in the stage of gathering data and establishing morphological relationships which precede the emergence of hypotheses and elaborated theories. We need to fully characterize the Sun's behaviour first before we can explain it. Yet it may be speculated that phase locking plays a role in establishing the association between sunspot extrema and RSIs. The waxing and waning sunspot activity constitutes an oscillation as well as the Sun's motion about the center of mass. These oscillations may be considered coupled as they belong to the same system, the Sun's dynamics. As coupled oscillators obey the principle of least action, they are bound to establish a state of minimal energy waste. Complete or partial phase locking contributes to such an economical state. In the phase locking process, consecutive RSEs, which are produced by the Sun's oscillations at equal distances, could be looked at as fixed points which serve as synchronizing signals. As symmetry breaking occurs in such cases (Strogatz and Stewart, 1993), it may be expected that on occasion the emerging pattern deviates from the most frequent outcome.

Statistical analysis shows that the connection between sunspot extrema and SPs is far from being random. The high density plot in Figure 2 shows the distribution of SPs in the period 1632-1990 in relation to a standard sunspot cycle of 11 years running from maximum to maximum. The position of SPs was measured within observed cycles of different length and then normalized to fit the standard cycle. Positions in the same phase of cycles of different length coincide in the normalized pattern. The position of the sunspot minimum, marked by an arrow, represents the normalized mean of minima positions in cycles observed between 1632 and 1990. Only two of the 33 investigated SPs do not fall within a range of ± 1.8 years around the sunpot minimum and ±1 year around the maximum. Their position is at 2.5 and 8.9 years in the standard cycle. The date of the first one is 1677.3. It coincides with the lowest phase of the Maunder minimum when it was difficult to assess the date of extrema. The date of the second one is 1945.6. It marks the transition from the regime of minima to that of maxima and is closer to the maximum.

The SPs around maxima concentrate on a range of 8 to 12 months before and after the maximum and shun the exact maximum phase. The association of SPs with the sunspot minimum shows a similar pattern. There are accumulations around 5.3 and 7.6 years, 1 year before and 1.3 years after the minimum, but the exact minimum phase is empty, and in the year afterwards only two SPs are to be found. Conspicuous is the skewed distribution around the minimum. Eighteen harmonics fall before it and only 7 after it. This could be important for prediction experiments. That there are only 6 connections with maxima and 25 with minima could be an effect of the relatively short time series of RSIs.

Considering whether the relationship between SPs and extrema of the sunspot cycle, covering nearly 360 years, is statistically significant, it has to be taken into account that two cyclical phenomena of nearly equal period are being compared each of which is neither random nor independent. So it is appropriate to restrict the analysis to the likelihood of synchrony between the two series. The question is what happens when the exact date of RSEs is subjected to displacements in time. To solve this problem by experiment, I shifted the respective RSE dates 1, 2, 3, 4, and 5 years ahead and back in time and computed the respective positions of the resulting SPs within observed sunspot cycles of different length as before with the true RSE. In each case I got 33 positions for the period 1632-1990 that were normalized to fit the standard cycle of 11 years. The complete set of shifted SPs, complemented by those related to the true RSEs, comprises 363 data distributed within the standard cycle. When this set was divided in five equal parts and subjected to the robust non-parametric Pearson test to check the hypothesis of a random distribution, the result was nearly perfect randomness: x² — 0.4 (4 deg of freedom); P = 0.98. Division of the data set in 10 and more parts yielded similar results. However, the set presented in Figure 2, linked to the true RSEs, is not at all consistent with a random distribution. When the Pearson test was applied in the same way as before, it yielded x² = 30.8 (4 deg of freedom and application of Yates's correction for continuity); P = 3.4 x 10~⁶. As the close connection of the true SPs with minimum and maximum in the standard cycle is clearly visible in Figure 2, it is justified to state that the statistical significance of the relationship goes beyond the level P = 0.001. When the RSIs are analysed separately, both show nearly the same highly significant frequency distribution. In the RS cycle 1811-1989, based on homogeneous sunspot observations, the mean of the deviations of sunspot extrema from SPs m_d = —0.05 and the standard deviation s — 0.87.

This statistical corroboration, linked to a physical background, justifies a forecast experiment. Though there are no reliable indications in the pattern when a switch from sunspot maxima to minima will occur, recent data can be used to decide whether the next SPs will go along with minima or maxima. The last minimum occurred in 1996.4. Even if the current cycle 23 had a length of only 10 years, which is not likely because of its relative weakness, the next minimum would fall at 2006.4. This is 4.9 years away from the next SP in 2001.5. Minima observed since 1632 did never deviate more than 1.8 years from the SP date. So the next SP should be associated with a maximum. Figure 2 shows that in most cases the actual maxima fall in a range 8 to 12 months before the exact SP date. So the imminent maximum will probably occur around 2000.6 ± 0.16 years. Even if cycle 24_;.had also a length of 10 years, the following minimum would occur in 2016.4. This does not match the SP in 2012.7. So another maximum should be expected around 2011.8 ±0.16 years.

Further inspection of the data indicates that not only the epochs of sunspot extrema, but also the intensity of sunspot activity may be read from RSIs. Figure 3 shows superimposed smoothed sunspot data from the two investigated RSIs. Prevalent antisymmetry of the trendlines in the consecutive RSIs is obvious. Details of these oppositely directed trends can be identified in Figure 1. Only the short period between the 130th and 145th year of the respective RSIs is an exception. The parallel course was initiated just at the time of the switch from minima to maxima after the 13th SP. It is a striking feature that in both of the RSIs the sunspot numbers reach the highest observed values a decade after the switch: R = 159 in 1778 and R = 201 in 1957. If this is a substantial repeat pattern, the sunspot amplitudes in the running RSI should roughly follow the course in RSI 1632 to 1810. A forecast experiment could help to decide whether this is correct. It should be expected that the current cycle with medium strength (R ^ 100) is followed by four to five weak cycles (R < 80). If this turns out to be correct, there is a good chance that the antisymmetric pattern is real. It could also be predicted that sunspot activity comparable to that of 1778 and 1957 should occur again around 2136, but who would check this forecast?

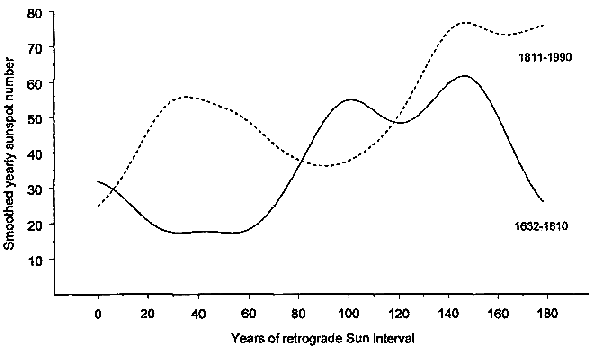
Figure 3. Superimposed smoothed sunspot numbers within consecutive retrograde Sun intervals 1632 -1810 and 1811-1990. The two curves, representing long-range trends in sunspot intensity, show prevalent antisymmetry, details of which are apparent in Figure 1. The exceptional parallel trend between the 130th and 145th year of the intervals is linked to the coherent switch from minima to maxima visible in Figure 1. Both of the curves reach their highest point at the end of the parallel trend. This corresponds with record sunspot numbers R = 159 in 1778 and R = 201 in 1957. If the connection is real, the interval that began in 1990 should roughly reflect the course of the interval starting in 1632. After cycle 23 of medium intensity, four to five weak cycles (R < 80) should follow.

The lack of elaborate theory does not impair the heuristic importance of the results. The hitherto unknown connection between retrograde phases in the Sun's irregular motion about the center of mass of the solar system and the timing of extrema in the 11-year sunspot cycle opens up a possibility to make forecasts of epochs of sunspot minima and maxima several decades ahead. The antisymmetrical repeat pattern of sunspot intensity emerging in consecutive retrograde Sun intervals seems to provide a means of developing a long-range forecast of the strength of sunspot activity. Further research is necessary to improve the understanding of the interconnections involved.

I thank an engaged anonymous referee for pointing out errors and making constructive suggestions.

Published on http://bourabai.narod.ru/ according permission of Frau Christiane Landscheidt