
Immanuel Kant (1724-1804)
Kant's most original contribution to philosophy is his "Copernican
Revolution," that, as he puts it, it is the representation that makes the object
possible rather than the object that makes the representation possible. This
introduced the human mind as an active originator of experience rather than just
a passive recipient of perception. Something like this now seems obvious:
the mind could be a tabula rasa, a "blank tablet," no more than a
bathtub full of silicon chips could be a digital computer. Perceptual input must
be processed, i.e. recognized, or it would just be noise -- "less
even than a dream" or "nothing to us," as Kant alternatively puts it.
But if the mind actively generates perception, this raises the question
whether the result has anything to do with the world, or if so, how much. The
answer to the question, unusual, ambiguous, or confusing as it would be, made
for endless trouble both in Kant's thought and for a posterity trying to figure
him out. To the extent that knowledge depends on the structure of the mind and
not on the world, knowledge would have no connection to the world and is not
even true representation, just a solipsistic or intersubjective fantasy.
Kantianism seems threatened with "psychologism," the doctrine that what we know
is our own psychology, not external things. Kant did say, consistent with
psychologism, that basically we don't know about "things-in-themselves," objects
as they exist apart from perception. But at the same time Kant thought he was
vindicating both a scientific realism, where science really knows the
world, and a moral realism, where there is objective moral obligation,
for both of which a connection to external or objective existence is essential.
And there were also terribly important features of things-in-themselves that we
do have some notion about and that are of fundamental importance to human
life, not just morality but what he called the three "Ideas" of reason:
God, freedom, and immortality. Kant always believed that the rational
structure of the mind reflected the rational structure of the world, even of
things-in-themselves -- that the "operating system" of the processor, by modern
analogy, matched the operating system of reality. But Kant had no real argument
for this -- the "Ideas" of reason just become "postulates" of morality -- and
his system leaves it as something unprovable. The paradoxes of Kant's efforts to
reconcile his conflicting approaches and requirements made it very difficult for
most later philosophers to take the overall system seriously.
Nevertheless, Kant's theory does all sorts of things that seem appropriate
for a non-reductionistic philosophical system and that later philosophy has had
trouble doing at all. Kant managed to provide, in phenomenal
reality (phaenomena="appearances"), for a sphere for science that was
distinct and separate from anything that would relate to morality or religion.
The endless confusion and conflict that still results from people trying to
figure out whether or how science and religion should fit together is deftly
avoided by Kant, who can say, for instance, that God and divine creation cannot
be part of any truly scientific theory because both involve
"unconditioned" realities, while science can only deal with conditioned
realities. In the world, everything affects everything else, but the traditional
view, found even in Spinoza,
is that God is free of any external causal influences. Similarly, Kant can be a
phenomenal determinist with science yet simultaneously allow for free
will, and that in a way that will not be entirely explicable to us -- a
virtue when the very idea of a rational and purposive free will, and not just
arbitrary choices, has involved obscurities that no one has been able to
resolve. Kant's theory prevents psychological explanations for behavior, however
illuminating, being used to excuse moral responsibility and accountability.
Thus, the tragic childhood of the defendant, however touching and
understandable, cannot excuse crimes commited in full knowledge of their
significance.
Kant's approach is also of comparative interest because of the similar
ancient Buddhist
philosophical distinction between conditioned realities, which mostly means the
world of experience, and unconditioned realities ("unconditioned
dharmas"), which interestingly include, not only the sphere of salvation,
Nirvana, but also space, which of course for Kant was a form imposed a
priori on experience by the mind.
The problems that must be sorted out with Kant are at the same time
formidable. Most important is the confusion that results from Kant mixing
together two entirely different theories in the Critique of Pure Reason
(1781). The first theory is that the fundamental activity of the mind, called
"synthesis," is an activity of thought that applies certain
concepts to a previously given perceptual datum from experience. It is
upon this theory that the Critique of Pure Reason was planned with its
fundamental division between the "Transcendental Aesthetic," about the
conditions of perception (what Kant called empirical "intuition"), and
the "Transcendental Logic," about the conditions of thought. Thus, Kant
still says, as late as page 91 of the first edition ("A"), "But since intuition
[Anschauung] stands in no need whatsoever of the functions of thought,
appearances [Erscheinungen] would none the less present objects to our
intuition" (A 90-91, Norman Kemp Smith translation, 1929, St. Martin's, 1965),
without, that is, any need for mental synthesis.
However, right in the middle of his subsequent argument for why cerain
concepts would be necessary and known a priori with respect to experience
(the "Transcendental Deduction"), Kant realized that "synthesis" would have to
produce, not just a structure of thought, but the entire structure of
consciousness within which perception also occurs. Thus he says, "What is first
given to us is appearance. When combined with consciousness [Bewußtsein],
it is called perception [Wahrnehmung]" (A 119-120). It is the structure
of consciousness, through synthesis, that turns "appearances" into objects and
perceptions, without which they would be nothing. Consequently Kant made
synthesis a function of imagination rather than thought, as a bridge
between thought and perception, though this creates its own confusions (it still
depends on the forms of thought and is still treated in the Logic). This move
occurred because Kant hit upon the idea that synthesis produced the unity that
we actually find in "apperception," i.e. in the unity of consciousness --
everything I know, think, see, feel, remember, etc. belongs to my
consciousness in one temporal stream of experience. Synthesis therefore
brings things into consciousness, making it possible for us to subsequently
recognize that our consciousness exists and that there are things in it.
Hume had described the result as
"something betwixt unity and number," since it is paradoxically one thing and
many things all at the same time.
These were all revolutionary ideas, exploring both the logical and the
psychological principles on which the complex whole of consciousness could be
generated, but they tore up Kant's original plan for his system so much that he
was never quite comfortable with them. He then tried to paper over his most
daring insights when he came to write both the Prolegomena to any Future
Metaphysics (1783) and the changes that he introduced into the second
edition of the Critique itself (1787, "B"). Thus Schopenhauer, who understood the
meaning of Kant's change of approach, advised his readers that they would be
wasting their time unless they obtained an edition of the Critique that
included the whole text from the first edition. It is now standard to include
both versions, with the original paginations in the margins.
The path to resolving the paradoxes of Kant's theory opens up with two basic
realizations: (1) Kant always believed that reason connected us
directly to things-in-themselves, and (2) Kant's system is not a Cartesian theory of
hidden, transcendent objects, but a version of empirical realism, that we
are directly acquainted with real objects. Kant's notion that reason connects us
directly to things-in-themselves does not allow for speculative metaphysics as
practiced by the Rationalists because reason alone does not determine any
positive content of knowledge ("Thoughts without content are empty; intuitions
without concepts are blind," A 51). For that some datum is required. Kant
allows that we possess two sources of input that can serve as such a datum,
physical sensation and the sense of moral duty. Physical sensation
precipitates an application of reason to experience, producing the perception of
phenomenal objects. The supreme rational expression of this is science. The
sense of moral duty precipitates an application of reason that generates ethics
and religion. The supreme rational expression of this is the "Postulates of
Practical Reason," the "Ideas" of God, freedom, and immortality which, to Kant,
are required as conditions of the the Moral Law.
The differences between reality as seen in science and reality as seen in
morality and religion reveal that there are aspects to existence that are not
revealed by either datum alone. The two sources are also unequal in the
magnitude and ultimate significance of their content. What science can
investigate and know is apparently all but endless, but it still leaves us
wondering, "What is it all for?" Morality and religion have a far more
limited rational content, returning to many of the same issues over and over
again, but such issues happen to include, not just the questions about
how to live, but the ultimate questions about the meaning of life and
existence ("Life, the Universe and Everything," in the memorable formula of
Douglas Adams). That our moral datum does not lead to direct, positive knowledge
of things that we are able to conceive, like God, leads Kant to characterize his
system as transcendental
idealism, that we have a subjective representation of such things,
without the real intuition that we have of physical objects. The reality
revealed by morality is thus for Kant a matter of faith (Glaube), an
inference from the Moral Law which is itself present to us with an
inexplicable authority. "Transcendental idealism" is thus profoundly
different from other forms of "idealism," like the "subjective idealism" of
Berkeley (what Kant called "empirical idealism") or the "objective idealism" of
Hegel, both of which offer
speculative certainties about the ultimate nature of things, which Kant does not
do. The nature of things that we can know about concretely, for Kant, is
revealed by science. Hence, Kantian transcendental idealism is equally attended
by empirical realism.
How Kant can be certain that reason connects us directly to
things-in-themselves is an question that he cannot answer. All that the
Transcendental Deduction aimed at was showing that particular concepts, like
causality or substance, are "necessary conditions for the possibility of
experience." If successful, the Deduction limits the application of the concepts
to experience, which is fine for Kant's philosophy of science, but doesn't help
when he turns to morality and the "Postulates of Practical Reason." There his
basic, but unjustified, theory of reason emerges. This shortcoming is what was
directly addressed and answered by Jakob Fries, whose epistemology
thus could save the generality of Kant's theory without falling back, like
Hegel, into speculative metaphysics.
That Kant's theory is one of empirical realism is difficult to
understand and easily forgotten. Since phenomena are undoubtedly mental
contents, a point repeatedly stressed by Kant, it is natural and easy to
infer from this a Cartesian "transcendental realism," according to which "real"
objects, which are not mental contents, are things that we do not experience. A
transcendental realism clearly contradicts Kant's transcendental idealism, but
we can still be left thinking that what we really have is an empirical
(subjective) idealism with a kind of transcendental agnosticism -- we don't know
transcendent Cartesian objects, but they are the real objects (the Greek
ontôs ónta, "beingly beings"). The lack of clear settlement in this area
of basic ontology is the most intractable problem in Kant's philosophy.
The situation, however, is not unique to Kant. Something very similar can be
found in Chinese T'ien-t'ai Buddhism (Japanese Tendai), as formulated by the
great Chih-i (or Zhiyi, 538-597). There we find the doctrine of
the "three truths" of "Emptiness" (neither existence nor non-existence nor both
nor neither), "conventional existence," and "the Middle." "Emptiness" is rather
like Kantian things-in-themselves where "dialectical illusion" is revealed by
the Antinomies (a device
similar to that employed by Nagârjuna, c.200 AD); "conventional
existence" is empirical realism; and "the Middle" the Buddhist reconciliation of
the two -- not a Hegelian "synthesis" because no absolute knowledge is produced
to overcome the inconceivablility of Emptiness.
Such a religious doctrinal tradition, however, may not be considered by many
to be very helpful with modern philosophical problems; and the T'ien-t'ai
"Middle," however consistent with the paradoxes of Buddhist philosophy, is not a
marked improvement over the balancing act in which Kant himself leaves us. The
solution to the dilemma was grasped by Schopenhauer but not otherwise well
understood by Kantians: Consciousness does not just condition knowledge
and perception, it conditions external reality. The modern context the
most like this is in quantum
mechanics, where, at least according to Niels Bohr, objects exist in a
certain way, as discrete actualities, because they are observed.
Otherwise, reality exists independently only as a sum of possiblities (where
Schrödinger's Cat can be both dead and alive). This is not exactly what we get
in Schopenhauer, who simplified matters by completely eliminating individuality
from the thing-in-itself: Individuality only occurs in space, the
principium individuationis. That, however, also eliminated any
possibility of individual immortality, which Kant thought was rather important.
I do not think, indeed, that much progress has been made beyond that. Something
new is required, as suggested in The Origin of Value in a Transcendent
Function, "Ontological
Undecidability," and "A New
Kant-Friesian System of Metaphysics." If neither subject nor object,
internal nor external, are ontologically fundamental, then we can stop worrying
about in which place the real things really are, and the threat of either
transcendental realism or empirical idealism disappears. This again sounds like
what might be needed in quantum mechanics, and a Kantian quantum mechanics
could offer hope both for the physics and metaphysics.
That brings us back to the datum of morality. Indeed, Kant's whole
system does seem to come down to his own famous words, inscribed on his tomb,
the "starry heavens above and the moral law within." If the existence of
morality is as evident as the existence of physical objects, then Kant's
dualism (empirical and transcendental) is required. If the existence of morality
is not so evident, as with Nietzsche and currently
fashionable nihilism, then there seems to be nothing left to motivate Kant's
concern with transcendent objects.
| Major Works |
date |
age |
Thoughts on the True Estimation of
Living Forces |
1746 |
22 |
| On Fire [Doctoral Dissertation] |
1755 |
31 |
A New Explanation of the First
Principles of Metaphysical
Knowledge
[Habilitation] |
1755 |
31 |
General Natural History and
Theory of the Heavens |
1755 |
31 |
| Physical Monadology |
1756 |
32 |
| New Theory of Motion and Rest |
1758 |
34 |
Some Experimental Reflections about
Optimism |
1759 |
35 |
The False Subtlety of the Four
Syllogistic Figures Demonstrated |
1762 |
38 |
Enquiry into the Clarity of the Principles
of Natural Theology and
Morality |
1762, 1764 |
38 |
On the Only Possible Argument for
Proving the Existence of God |
1763 |
39 |
Attempt to Introduce the Concept of
Negative Quantitites into
Philosophy |
1763 |
39 |
Observations on the Feeling of the
Beautiful and Sublime |
1764 |
40 |
Dreams of a Visionary, Explained by
Dreams of Metaphysics |
1766 |
42 |
The First Ground of the Distinction of
Regions in Space |
1768 |
44 |
On the Form and Principles of the
Sensible and the Intelligible
World
[Inaugural Dissertation] |
1770 |
46 |
| Critique of Pure Reason |
1781, 1787 |
57 |
Prolegomena to Any
Future
Metaphysics |
1783 |
59 |
| Idea for a Universal History |
1784 |
60 |
| What is Enlightenment? |
1784 |
60 |
Foundations of the Metaphysics
of
Morals |
1785 |
61 |
Metaphysical Foundations of
Natural
Science |
1786 |
62 |
Conjectural Beginning
of Human History |
1786 |
62 |
| Critique of Practical
Reason |
1788 |
64 |
| Critique of Judgment |
1790, 1793 |
66 |
Religion Within the Limits
of Reason
Alone |
1793, 1794 |
69 |
| The End of All Things |
1794 |
70 |
| Perpetual Peace |
1795, 1796 |
71 |
| The Metaphysics of Morals |
1797,
1798-1803 |
73 |
| The Strife of the Faculties |
1798 |
74 |
Anthropology from a
Pragmatic Point of View |
1798 |
74 |
| Logic |
1800 |
76 |
But something that Kant overlooks is the
Platonic overtone of his own famous statement. The "starry heavens" are
especially striking, even for Kant, because they are beautiful. Most
people see them, not as factual objects of science, but as things of awe,
wonder, mystery, and beauty. Unfortunately, the mature Kant does not have the
aesthetic realism of Plato and Schopenhauer, or of the younger Kant himself (in
the Observations on the
Feeling of the Beautiful and Sublime, 1764). To Plato, the beauty of
things is a clue to the transcendent; but the mature Kant decided that only
morality played that part. This only reinforces Kant's moralism and weakens his
overall theory of value, let alone the metaphysics into which that fits.
The hope of fixing the loose ends of transcendental idealism, and of giving
morality itself a credible realistic basis, lies back in the consideration of
empirical realism. The unresolved paradox of a "realism" that was also a
phenomenalism is the root of the greater difficulties considered above and below. If objects are
immanent in experience but independent in their existence, then clearly there is
a transcendent aspect to them, however that is construed. God, freedom, and
immortality are not actually essential to that, and Schopenhauer did not
believe in any of them; but Schopenhauer also overlooked Kant's analysis of
"conditioned" versus "unconditioned" objects. Even a physical object, the
universe, passes beyond experience and generates metaphysical paradoxes (the Antinomy of space and time),
in so far as it is, in its entirety, an unconditioned whole. This is really just
what Kant's Ideas are all about. All these matters in Kant's thought are
therefore still open to clarification and development, as Fries and Schopenhauer
attempted immediately, and as considered elsewhere in these pages.
Despite, but also because of, the paradoxes of his thought, much of
philosophy in the Twentieth Century has been ill conceived knock-offs of Kant's
theory. The idea that the mind produces the world it knows conspicuously turns
up in Wittgenstein's theory of
language and now with tedious, endless repetition in "post-modern" theories that
see all reality as "socially constructed" on the basis of no more than "power"
relationships (ultimately derived from the Marxist notion of ideological
"superstructures" to class and economic relations). These all produce a
fundamental paradox that was avoided by Kant, for they are all relativistic and
subjectivist denials that knowledge even exists, which nevertheless maintain
that this circumstance is a fact that can be known and demonstrated with
some certainty -- though the "edifying" version of this recognizes the paradox
by not trying such a demonstration, while still expecting us to accept the
conclusion (!?). Thus, Wittgenstein sees all reality as created by particular
languages, even though one might think this would imply that truths about
language would be created by particular languages also. And since common sense
expressed in most historical languages has actually affirmed that the world
exists independently of what we say or think about it, this should mean that it
does. Kant, of course, does not see the process of synthesis producing anything
relativistic or subjectivist: the realism of phenomena is fully meant. The
knock-offs of Kant are rarely realistic.
While the knock-offs occupy fashionable opinion, basic misconceptions about
Kantian theory are casually perpetuated. For instance, a defining characteristic
of Kantian philosophy is that synthetic a priori propositions are
not self-evident and can be denied without contradiction.
What makes them true a priori is that they have a cognitive ground which
is not in empirical intuition (i.e. perception). Although it is often claimed,
as by the great French mathematician Poincaré, that the existence of
non-Euclidean geometry refutes Kant's philosophy of geometry, in fact Kant's
view of the nature of the axioms of geometry as synthetic a priori
propositions means that Kant could have predicted the existence of
non-Euclidean geometry. This should be obvious given any clear understanding of
the meaning of "synthetic." Only Leonard Nelson fully appreciated
this circumstance. The question of geometry in Kant is addressed in "The Ontology and Cosmology of
Non-Euclidean Geometry."
A striking thing about Kant's life is how late he began his most significant
work. He didn't complete his doctoral thesis and "habilitation," by which one
qualified to teach in a German university, until 1755, when he was already 31
years old, having previously made a living as a tutor -- at such an age
mathematicians and physicists are usually expected to have already burnt out.
Kant's position, however, was still only a Privatdozent, which meant he
was only paid by the student, and carried an academic teaching load that today
would only be found in a community
college. This difficult life only improved in 1770, when Kant finally was
appointed to a regular chair of philosophy, at age 46. Nevertheless, Kant had
already made a name for himself with his often original ideas in physics and
astronomy and with his growing critique of the widely accepted, at least in
Germany, thought of Leibniz
(e.g. the seminal "The First Ground of the Distinction of Regions in Space,"
which upheld Newtonian arguments against Leibniz's
denial of the existence of space).
The "Inaurgural Dissertation" that commemorated his appointment was the first
real step towards the characteristic doctrines of the Critical
Philosophy. Working that out, and writing the Critique of Pure
Reason, still hampered by heavy teaching obligations, then took more than
ten years. That book's publication in 1781 put Kant, at age 57, on the doorstep
of a vast philosophical project, whose details he had already planned, but whose
completion his age and health -- he was never a very robust man -- might well
frustrate. His concern that he might actually die before finishing his work, in
an age when sudden death was an all too familiar phenomenon, led him to
concentrate his efforts with a discipline that has led to caricatures of him
ever since -- his clock-like appearance for his daily constitutional, on what
then became the "Philosopher's Walk" in Königsberg, is usually seen as evidence
of habits mechanical to an absurd extent, rather than the caution and discipline
of a frail and aging soul desperate to finish his life's work. His previous
custom of dining out and enjoying conversation with his friends was sacrificed
in the race against death. What his life had been like we learn from Ernst
Cassirer:
"Thus," [F.T.] Rink says, "Kant in his early years spent almost
every midday and evening outside his house in social activities, frequently
taking part also in a card party and only getting home around midnight. If he
was not busy at meals, he ate in the inn at a table sought out by a number of
cultured people." Kant gave himself to this mode of life in such an easy and
relaxed way that even the most meticulous psychological observer among his
intimates was occasionally puzzled about him; in 1764 [Johann Georg] Hamann
says that Kant carries in his head a host of greater and lesser works, which
he however probably will never finish in the "whirl of social distraction" in
which he is now tossed. [Kant's Life and Thought, translated by James
Haden, Yale University Press, 1981, pp.51-52]
The race with death, happily, was won, and the key monuments of the Critical
Philosophy, including the trilogy of Critiques, were produced. It was
declining faculties that finally stilled his pen, before he actually passed
away. Kant's grave has fortunately escaped the destruction that the Soviet
occupation visited upon the sights of traditional Königsberg. Now that the
city's Soviet name, Kaliningrad, awkwardly still commemorates the Stalinist
President of the Soviet Union, but the Russians do not want to return the city
to its German name, the proposal has been floated to actually name the city
after Kant (i.e. Kantgrad). Since Kant's thought is truly the watershed of modern philosophy,
and still the fruitful point of departure for the 21st century, no such monument
could be more suggestive, encouraging, and hopeful.
I have enjoyed the good fortune to know a philosopher, who was my
teacher. In the prime of life he had the happy cheerfulness of a youth, which,
so I believe, accompanied him even in grey old age. His forehead, formed for
thinking, was the seat of indestructible serenity and peace, the most
thought-filled speech flowed from his lips, meriment and wit and humor were at
his command, and his lecturing was discourse at its most entertaining. In
precisely the spirit with which he examined Leibniz, Wolff, Baumgarten, and
Hume and purused the natural laws of the physicists Kepler and Newton, he took
up those works of Rousseau which were then appearing, Émile and
Héloïse, just as he did every natural discovery known to him, evaluated
them and always came back to unprejudiced knowledge of Nature and the moral
worth of mankind. The history of nations and peoples, natural science,
mathematics, and experience, were the sources from which he enlivened his
lecture and converse; nothing worth knowing was indifferent to him; no cabal,
no sect, no prejudice, no ambition for fame had the least seductiveness for
him in comparison with furthering and elucidating truth. He encouraged and
engagingly fostered thinking for oneself; despotism was foreign to his mind.
This man, whom I name with the utmost thankfulness, and respect, was Immanuel
Kant; his image stands before me to my delight. [Johann Gottfried Herder,
Letters on the Advacement of Humanity, letter 79, quoted by Cassirer,
op cit., p. 84]
Kant's Transcenental
Idealism
Analytic and Synthetic:
Kant and the Problem of First Principles
Three Points in Kant's
Theory of Space and Time
Kant's First Antinomy, of
Space and Time
Kantian Quantum
Mechanics
Intuition and Mysticism
in Kantian Philosophy
Psychological Types
History of Philosophy
Home Page
Copyright (c) 1996, 1998, 2000, 2002, 2003, 2004 Kelley L. Ross, Ph.D. All Rights Reserved
Analytic and Synthetic: Kant and the Problem of First
Principles
Except for outright Skeptics, Aristotle's
solution to the Problem of First
Principles, that such propositions are known to be true because they are
self-evident, endured well into Modern Philosophy. Then, when all the
Rationalists, like Descartes, Spinoza, and Leibniz, appealed to
self-evidence and all came up with radically different theories, it should have
become clear that this was not a good enough procedure to adjudicate the
conflicting claims. This awkward situation was then blown apart by Hume, under
whose skeptical examination, reviving the critique of al-Ghazâlî, even the
principle of causality crumbled.
Kant does not directly pose the Problem of First Priniciples, and the form of
his approach tends to obscure it. Thus, the "Transcendental Logic" in the
Critique of Pure Reason is divided into the "Transcendental Analytic" and
the "Transcendental Dialectic." The "Dialectic" is concerned with the fallacies
produced when metaphysics is extended beyond possible experience. The
"Analytic," about secure metaphysics, is divided into the "Analytic of Concepts"
and the "Analytic of Principles." "Principles" would be Principia in
Latin, i.e. "beginnings," "first things," "first principles," where now in
English, thanks to the drift in the meaning of "principle," the term must be
reduplicated with an etymologically redundant "first." Kant,
however, is here writing in German, and in place of Principia we have
Grundsätze (singular Grundsatz, "principle," "axiom" -- literally
"ground sentence"). The examination of the Grundsätze, however, is
deferred until after and "Analytic of Concepts." Thus, were the Problem of First
Principles to be raised, it seems like that would come after an examination of
concepts. Since it is not raised at all, one is left with the impression that it
has somehow, along the way, actually already been dealt with. It has. [note]
The peculiarity of Kant's approach, from an Aristotelian (or Friesian) point of view, is not
idiosyncratic. Kant approaches the matter as he does because he is responding to
Hume, and one of Hume's intitial
challenges is about the origin of "ideas." While the Problem of First Principles
is about the justification of propositions, Hume's Empiricist approach goes back
to asking about the legitimacy of the very concepts, of which the propositions
are constituted, in the first place. The Rationalists never worried too much
about that. For Descartes, any notion that could be conceived "clearly and
distinctly" could be used without hesitation or doubt, a procedure familiar and
unobjectionable in mathematics. It was the Empiricists who started demanding
certificates of authenticity, since they wanted to trace all knowledge back to
experience. Locke was not aware, so much as Berkeley and Hume, that not
everything familiar from traditional philosophy (or even mathematics) was going
to be so traceable; and Berkeley's pious rejection of "material substance" lit a
skeptical fuse whose detonation would shake much of subsequent philosophy
through Hume, thanks in great measure to Kant's appreciation of the importance
of the issue.
Thus, Kant begins, like Hume, asking about the legitimacy of concepts.
However, the traditional Problem has already insensibly been brought up; for in
his critique of the concept of cause and effect, Hume did question the
principle of causality, a proposition, and the way in which he expressed
the defect of such a principle uncovered a point to Kant, which he dealt with
back in the Introduction to the Critique, not in the "Transcendental
Logic" at all. Hume had decided that the lack of certainty for cause and effect
was because of the nature of the relationship of the two events, or of the
subject and the predicate, in a proposition. In An Enquiry Concerning Human
Understanding, Hume made a distinction about how subject and predicate could
be related:
All the objects of human reason or enquiry may naturally be
divided into two kinds, to wit, Relations of Ideas, and Matters of
Fact. Of the first kind are the sciences of Geometry, Algebra, and
Arithmetic; and in short, every affirmation which is either intuitively or
demonstratively certain [note: these are Locke's categories]. That
the square of the hypothenuse is equal to the square of the two sides, is
a proposition which expresses a relation between these figures. That three
times five is equal to the half of thirty, expresses a relation between
these numbers. Propositions of this kind are discoverable by the mere
operation of thought, without dependence on what is anywhere existent in the
universe. Though there never were a circle or triangle in nature, the truths
demonstrated by Euclid would for ever retain their certainty and evidence.
Matters of fact, which are the second objects of human reason, are not
ascertained in the same manner; nor is our evidence of their truth, however
great, of a like nature with the foregoing. The contrary of every matter of
fact is still possible; because it can never imply a contradiction, and is
conceived by the mind with the same facility and distinctness, as if ever so
conformable to reality. That the sun will not rise to-morrow is no less
intelligible a proposition, and implies no more contradiction than the
affirmation, that it will rise. We should in vain, therefore, attempt
to demonstrate its falsehood. Were it demonstratively false, it would imply a
contradiction, and could never be distinctly conceived by the mind.
[Enquiries, Selby-Bigge edition, Oxford, 1902, 1972,
pp.25-26]
Both paragraphs warrant quoting in full. The first now would seem properly
more a matter of embarrassment than anything else. Whatever Hume expected from
intuition or
demonstration, it would be hard to find a mathematician today who would agree
that "the truths demonstrated by Euclid would for ever retain their certainty
and evidence." If Hume's fame rests on this point, there would be little to
recommend it. The second paragraph, however, redeems the impression by giving us
a logical criterion to distinguish between truths that are "relations of
ideas" and those that are "matters of fact": A matter of fact can be
denied without contradiction.
This was the immediate inspiration to Kant, who can have asked himself how
something "demonstratively false" would "imply a contradiction." A contradiction
means something of the form "A and not-A." If a proposition expressing a matter
of fact can be denied without contradiction, then the subject and the predicate
of such a proposition cannot contain anything in common, otherwise the item
would turn up posited in the subject but negated in the predicate of the denial.
On the other hand, a proposition that cannot be denied without
contradiction must contain something in the predicate that is already in the
subject, so that the item does turn up posited in the subject but negated in the
predicate of the denial. This struck Kant as important enough that, like Hume,
he founded a whole critique on it, and also produced some more convenient and
expressive terminology. Propositions true by "relations of ideas" are now
analytic ("taking apart"), while propositions not so founded are
synthetic ("putting together").
This clarified distinction Kant could then turn on Hume's own examples of
"relations of ideas." Can geometry be denied without contradiction? Kant did not
see that the predicates of the axioms of geometry contained any meaning already
expressed in the subjects. They were synthetic. They could be denied without
contradiction. Geometry would thus not have an intuitive self-evidence or
demonstrative certainty that Hume claimed for it. Kant still thought that
Euclid, indeed, would have certainty, but the ground of certainty would have to
located elsewhere. Nevertheless, Kant is rarely credited, and Hume rarely
faulted, for their views of the logic of the axioms of geometry. If the axioms
of Euclid can be denied without contradiction, this means that systems of
non-Euclidean geometry are logically possible and can be constructed without
contradiction. But it is not uncommon to see the claim that Kant actually denied
this, and it is Kant, not Hume, who is typically belabored for implicitly
prohibiting the development of non-Euclidean systems. This distortion can only
come from confusion and bias, a confusion about the meaning of "synthetic" (even
in Hume's corresponding category), and a bias that the Analytic tradition has
for British Empiricism, by which the glaring falsehood of Hume's statements is
ignored and Kant's true and significant discovery misrepresented. This curious
and reprehensible turn is considered in detail elsewhere.
Kant, as it happens, also did not see how arithmetic could be analytic. In
his own example of "7 + 5 = 12" (p. B-15), if "7 + 5" is understood as the
subject, and "12" as the predicate, then the concept or meaning of "12" does not
occur in the subject. This was rather harder to swallow than the point about
geometry, for it seems rather "intuitively" certain that "7 + 5 = 12" cannot be
denied without contradiction. Kant must have missed something. Hope for
demonstrating the analytic nature of arithmetic came with the development of
propositional logic, since a proposition like "P or not P" clearly cannot be
denied without contradiction, but it is not in a subject-predicate form. Still,
"P or not P" is still clearly about two identical things, the P's, and "7 + 5 =
12" is more complicated than this. But, if "7 + 5 = 12" could be derived
directly from logic, without substantive axioms like in geometry, then its
analytic nature would be certain. In their Principia Mathematica
(1910-1913), Russell and Whitehead and, in the Tractatus, Wittgenstein thought that they
could indeed derive arithmetic from logic. Their demonstrations, however, were
flawed, and it turned out that substantive axioms were necessary, just like in
geometry. The axioms are now those of axiomatic Set Theory, and it is Set Theory
that concerns the foundations of arithmetic. Kant turned out to be right again,
though, curiously, he is again rarely credited for this.
Kant's discovery, however, can be trivialized if it turns out that there are
simply no analytic propositions at all. This task was undertaken by
Willard Van Orman Quine ("Two Dogmas of Empiricism," 1950). The approach, simply
enough, was Nominalistic. If
we say that "red is a color" is an analytic proposition, where is "color" in
"red"? I don't see it. If we say that the meaning "color" is in the
meaning of "red," where are these "meaning" things? I don't see them.
Thus, if language consists of words but not abstract meanings, then we don't
have to worry about one meaning containing another. "Red is a color" is just a
convention of our language, which is even what we can say about "P or not P."
Besides the general failings of Nominalism, Quine's particular critique is well
refuted by Jerrold Katz.
In Kant there is little left in the category of "analytic." Definitions and
truths of logic are going to be about it; and the definitions themselves
will be suspect when the concepts defined may or may not be legitimate. The
meaning within a concept must also in some sense be "put together," and the
ground of this will raise the same questions as the ground of synthetic
propositions. Thus, Saul Kripke began to speak of "analytic a posteriori"
propositions, when the meanings in the subject are themselves united on only
a posteriori grounds, i.e. the basis of experience. Indeed, dictionary
definitions of natural language words are prima facie of conventional
usage, e.g. how a pot is different from a pan, and the meaning of any words can
be simply stipulated for some appropriate purpose, e.g. a "designated
hitter" can go to bat for some particular member of a baseball team (usually the
pitcher), without otherwise replacing him in other play. Thus, a big fight over
the existence of analytic propositions doesn't in the end make that much
difference. Synthetic propositions are the key anyway, as they were if Kant
wanted to answer Hume's critique of causality.
For, indeed, outside of an axiomatized logic itself, the First Principles of
Demonstration will be synthetic. However Kant can explain the truth of
non-empirical synthetic propositions, i.e. those that are a priori
instead of a posteriori, that will be his answer to the Problem of First
Principles. They are clearly now, after Hume, not going to be self-evident. Yet
Hume himself is often poorly understood. While it is common to say that Hume
denied the existence of synthetic a priori propositions, there is some
question about whether he actually does. He says that the relationship of cause
and effect is not discovered or known by any reasonings a priori,
but that is not the same thing. A synthetic a priori proposition is not
known from any reasonings. In fact, Hume does not see that the relationship of
cause and effect is discovered or known from anything, since it is not
justified by experience, in which there is no necessary connection
between cause and effect, and there is in fact nothing in the cause to even
suggest the effect, much less than the effect must follow. Hume's famous
explanation was a psychological one, that we become accustomed to the
association of certain events ("causes") with others ("effects"); but this,
obviously, carries no weight whatsoever about the nature of things, which is
what makes Hume, very properly, a Skeptic.
At the same time, Hume had no doubts whatsoever of the necessity of
cause and effect. This is where he is commonly misrepresented. People assume
that because he was a Skeptic, then he must have thought it possible for causes
to occur without effects, i.e. for the principle of causality to be contradicted
in actuality. He never had any such expectation, and in fact he ruled out a
priori, not only miracles, but also chance and free
will just because they would violate (a very deterministic) causality.
Confusion over this occurs because people do not appreciate that Hume as an "Academic" Skeptic, holding
that lack of knowledge (the meaning of "Skepticism") does not rule out
"reasonable" beliefs. Causality is a "reasonable" belief because, as Hume says,
"All reasonings concerning matter of fact seem to be founded on the relation of
Cause and Effect" [Enquiry, op. cit., p. 26]. So without
it, we would have no basis of reasoning in daily life. Thus, Hume says:
Nor need we fear that this philosophy, while it endeavors to limit
our enquiries to common life, should ever undermine the reasonings of common
life, and carry its doubts so far as to destroy all action, as well as
speculation. Nature will always maintain her rights, and prevail in the end
over any abstract reasoning whatsoever. Though we should conclude, for
instance, as in the foregoing section, that, in all reasonings from
experience, there is a step taken by the mind which is not supported by any
argument or process of the understanding [i.e. from cause to effect]; there is
no danger that these reasonings, on which almost all knowledge depends, will
ever be affected by such a discovery. [ibid., p. 41]
Kant therefore understood that Hume's problem was not with the quid
facti, that there were causes and effects, and necessary connection, but
with the quid juris, the epistemic justification of the principle. While
some philosophers spent much of the 20th Century congratulating Hume for having
discovered that causality might not exist, they never seem to have noticed that
he explicitly denied having done anything of the sort. Kant already knew the
type, who "were ever taking for granted that which he doubted, and demonstrating
with zeal and often with impudence that which he never thought of doubting..."
[Prolegomena to Any Future Metaphysics, p. 259, Lewis White Beck
translations, Bobbs-Merrill, 1950, p.6].
Kant's solution to the quid juris in the Critique of Pure
Reason was the argument of the "Transcendental Deduction" (in the "Analytic
of Concepts") that concepts like causality are "conditions of the possibility of
experience," because they are the rules by which perception and experience are
united into a single consciousness, through a mental activity called
"synthesis." Once the existence of consciousness is conceded (which not
everyone, e.g. behaviorists, might be willing to do), then whatever is necessary
for the existence of consciousness must be conceded.
This is a strong argument and, decisive or not, is heuristically of great
value, especially when we untangle it from the earlier views of perception in
the Critique. However, it suffers from a couple of serious drawbacks. One
is that, like Hume's own explanation, it is a psychological approach that does
not necessarily tell us anything about objects, i.e. consciousness may be united
in a way that is irrelevant to external things. Kant seemed to recognize this
himself when he said that none of this gives us any knowledge of
things-in-themselves. This problem was never properly sorted out by Kant, and is
considered independently in "Ontological Undecidabilty".
The second drawback of Kant's argument is that it would only work, indeed,
for the "conditions of the possibility of experience," and not for any other
matters which might seem to involve synthetic a priori propositions. Hume
himself was just as concerned about morality as about causality, and found
himself in the same Skeptical position in both matters. The only comparable
thing that Kant can do for morality, however, would be to employ a principle of
the "conditions of the possibility of morality." But this would require
conceding that morality exists, which is something that a very large number of
people in the 20th century, far beyond behaviorists, would not be willing to do.
Nor does it make one a Kantian merely to vaguely appeal to human "rationality"
(e.g. John Rawls) as a basis for morality, since this really just begs the
question of justification -- besides violating Hume's famous observation
that propositions of obligation ("ought," imperatives) cannot be logically
derived from propositions of fact ("is," indicatives).
Keeping in mind that First Principles cannot be proven, and that synthetic
propositions can be denied without contradiction, the conspicious historical
alternatives seem to be to deny one or the other. Hegel denied the first, by taking
the equivalent of Kant's Transcendental Deduction as itself a part of
metaphysics and a proof, by means of novel principles of "dialectical" logic, of
moral and metaphysical truths. To an extent, Hegel may also have denied the
second, as Leibniz certainly
did, treating any moral or metaphysical truth as analytic, if only from the
point of view of divine omniscience. Either such move, however, cannot escape
the original embarrassments of Rationalism, or avoid the devastation inflicted
by the criticisms made by Hume and Kant.
Less conspicous historically was Jakob Fries, who could accept the
proper meanings of "First Principle" and of synthetic propositions. The Friesian
theories of deduction and of
non-intuitive immediate
knowledge make it possible to preserve the advances of Hume and Kant without
falling back into Rationalism or heading for the Nihilism (so different from
Hume's Skepticism), relativism, scientism, pragmatism, etc., so conspicuous in
the 20th century. Later, Karl
Popper proposed a special solution for the Problem in that science, by using
falsification, does not need to worry about a positive justification of First
Principles at all. This enables scientific progress to heedlessly continue, as
it has, regardless of the status of any philosophical solution.
Thus, Kant gave us the real elements of the solution of the Problem of First
Principles, even though he could not complete and seal the matter himself.
Indeed, no one can hope to do that, even as new elements and new understanding
of the solution emerge over time.
Epistemology
History of Philosophy
Home Page
Analytic and Synthetic: Kant and the Problem of First
Principles, Note
In his earlier writings, in Latin, Kant had actually used the Latin
expression principia prima, "First Principles." In the Critique of
Pure Reason, we get an explicit discussion of principia only at the
beginning of the "Transcendental Dialectic":
The term 'principle' [Prinzips] is ambiguous, and commonly
signifies any knowledge [Erkenntnis] which can be used as a principle
[Prinzips], although in itself, and as regards its proper origin
[Ursprung], it is no principle [Principium]. Every
universal proposition, even one derived from experience, through induction
[Induktion], can serve as major premise [Obersatz] in a
syllogism; but it is not therefore itself a principle [Principium].
[Norman Kemp Smith translation, St Martin's Press, 1929, 1965, p.301, A
300]
Here the difference between Kant's use of the German term and the Latin is,
shall we say, lost in translation -- an entirely unnecessary loss, since the
Latin term could have been used in English just as in German. Kant explains the
drift in meaning of "principle," but instead of contrasting principium
with principium primum, as in English we can contrast "principle" with
"first principle," he contrasts German Prinzips with Latin
Principium. By translating both the German term and the Latin one as
"principle," Kemp Smith obscures the difference between a principle, in the
modern sense, and a first principle. This may reveal that Kemp Smith actually
isn't very sensitive or interested in either first principles or the Problem of
First Principles. Indeed, Anglo-American philosophy, with its empiricist
tendencies, has not been attracted to anything so un-empirical as first
principles.
The passage also displays a bit of evidence that Kant takes the derivation of
universal propositions from experience through induction as unproblematic. He
cannot have been unaware of the Problem of Induction, having read Hume, but had
not worked out, as no one would until Karl Popper, that there is a
solution.
Return to text
Kant's Transcendental Idealism
The obscurity of Kant when it comes to his theory of empirical realism
and transcendental idealism is largely due to his terminology and the
difficulties of reconciling parts of his theory. Since "transcendental" is
contrasted with "empirical," the two terms are epistemological and mean
"independent of (i.e. transcending) experience" and "immanent in experience."
Since "realism" is contrasted with "idealism," those two terms are ontological
and mean "independent of my existence" and "dependent on my existence." Berkeley
was for Kant the characteristic "idealist," and undoubtedly an empiricist, while
Descartes was a "realist," believing commonsensically that objects exist
independent of us, but who also thought that we could only know their essences
through "clear and distinct" innate ideas, not experience. This made Descartes a
"transcendental" realist.
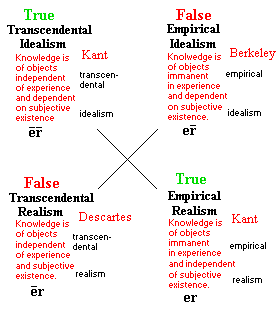 If we try to construct a square of opposition using Kant's
two distinctions, we have some trouble. A strictly constructed square of
opposition would look like the one at right. "Transcendental" (e)
is the negation of "empirical" (e), and "idealism" (r) is
the negation of "realism" (r). The structure we get, however, does not
work for Kant's theory. Transcendental idealism and empirical realism would be
contradictories and so cannot both be true, as Kant requires.
Similarly, transcendental realism and empirical idealism are also
contradictories and so cannot both be false, as Kant requires. The
features of the square of opposition that we would expect Kant's theory to
conform to would be that "contraries," the two upper members, are both false,
while the "subcontraries," the two lower members, are both true.
If we try to construct a square of opposition using Kant's
two distinctions, we have some trouble. A strictly constructed square of
opposition would look like the one at right. "Transcendental" (e)
is the negation of "empirical" (e), and "idealism" (r) is
the negation of "realism" (r). The structure we get, however, does not
work for Kant's theory. Transcendental idealism and empirical realism would be
contradictories and so cannot both be true, as Kant requires.
Similarly, transcendental realism and empirical idealism are also
contradictories and so cannot both be false, as Kant requires. The
features of the square of opposition that we would expect Kant's theory to
conform to would be that "contraries," the two upper members, are both false,
while the "subcontraries," the two lower members, are both true.
If we want such a square of opposition, it will have to be rearranged without
regard for the strict logical properties of the terms. We can save the
distinctions and do that by recalling that opposites contradict each other only
when applied to the same objects. Black coal and white snow are not
contradictions. Kantian realism and Kantian idealism are thus reconciled by a
distiction, that between phenomena and things-in-themselves. The former applies
to the former, and the latter to the latter.
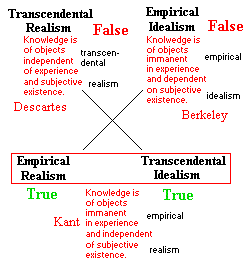 We can then produce a square
like the one at right, which allows for the traditional truth values. In this
version the definition of "transcedental idealism" has actually been left out.
Kant's position, although terminologically embracing the two lower members, is
really well defined by only one of them, empirical realism. However, saying that
the objects of knowledge are immanent in experience and independent of
our existence involves a paradox. How can something be independent in existence
and yet dependent or immanent in our experience, our representation?
We can then produce a square
like the one at right, which allows for the traditional truth values. In this
version the definition of "transcedental idealism" has actually been left out.
Kant's position, although terminologically embracing the two lower members, is
really well defined by only one of them, empirical realism. However, saying that
the objects of knowledge are immanent in experience and independent of
our existence involves a paradox. How can something be independent in existence
and yet dependent or immanent in our experience, our representation?
...the representation alone must make the object possible...
...representation in itself does not produce its object in so far as
existence is concerned... [A 92]
The common sense, direct acquaintance with objects, part of this is what Kant
appears to mean by his empirical realism, while the paradoxical, "in me but not
of me," metaphysics is what he means by "transcendental idealism." This is the
paradox addressed by Schopenhauer and by "Ontological Undecidability."
However, using the strict definitions, "transcendental idealism" means
something else, as reproduced in the entry at left.  If "transcendental" means,
epistemically, "independent of experience," but "idealism" means, ontologically,
"dependent on subjective (my) existence," then "transcendental idealism" would
have to mean knowledge of objects that are dependent on my existence but
independent of my experience. This seems to be, not just a paradox, but an out
and out contradiction, since if something exists as an epiphenomenon of myself,
it hardly seems like it could be independent of my experience. Berkeley's
principle was "to be is to be perceived," but this kind of "transcendental
idealism" would require that something is because of my existence but then is
not perceived. This might work on the basis of Spinoza's metaphysics, where my
existence is God's existence, but God's knoweldge far transcends mine.
Nevertheless, since anything is God, God is part of my experience after all.
If "transcendental" means,
epistemically, "independent of experience," but "idealism" means, ontologically,
"dependent on subjective (my) existence," then "transcendental idealism" would
have to mean knowledge of objects that are dependent on my existence but
independent of my experience. This seems to be, not just a paradox, but an out
and out contradiction, since if something exists as an epiphenomenon of myself,
it hardly seems like it could be independent of my experience. Berkeley's
principle was "to be is to be perceived," but this kind of "transcendental
idealism" would require that something is because of my existence but then is
not perceived. This might work on the basis of Spinoza's metaphysics, where my
existence is God's existence, but God's knoweldge far transcends mine.
Nevertheless, since anything is God, God is part of my experience after all.
What this peculiar meaning of "transcendental idealism" reveals  are the loosest ends of Kant's
thought. The terminology of "transcendental," "empirical," "realism," and
"idealism" does not seem well ordered for Kant's purposes, in part because those
purposes are unsettled. The contradiction of the strict rendering of
"transcendental idealism" might be resolved if we say that there is simply no
knowledge in this case, which is pretty much what Kant says about
things-in-themselves -- the soul certainly depends on my existence but is
not part of my experience because I don't have any knowledge of it. But then
Kant doesn't want to go all the way with that. Morality doesn't fit into
empirical reality, but then maybe that isn't too bad, since morality is really
"regulative" rather than "constitutive" (of metaphysical entities). What is bad
are "God, freedom, and immortality," which totally upset the applecart. If there
are such things, they are about transcendent objects which, at least in one
case, are independent of my existence. If they are only objects of "faith," we
want to know how that is motivated; and if they are motivated as necessary
conditions of the Moral Law, then it seems like they would be as much matters of
knowledge as the necessary conditions of experience, i.e. causality, substance,
etc.
are the loosest ends of Kant's
thought. The terminology of "transcendental," "empirical," "realism," and
"idealism" does not seem well ordered for Kant's purposes, in part because those
purposes are unsettled. The contradiction of the strict rendering of
"transcendental idealism" might be resolved if we say that there is simply no
knowledge in this case, which is pretty much what Kant says about
things-in-themselves -- the soul certainly depends on my existence but is
not part of my experience because I don't have any knowledge of it. But then
Kant doesn't want to go all the way with that. Morality doesn't fit into
empirical reality, but then maybe that isn't too bad, since morality is really
"regulative" rather than "constitutive" (of metaphysical entities). What is bad
are "God, freedom, and immortality," which totally upset the applecart. If there
are such things, they are about transcendent objects which, at least in one
case, are independent of my existence. If they are only objects of "faith," we
want to know how that is motivated; and if they are motivated as necessary
conditions of the Moral Law, then it seems like they would be as much matters of
knowledge as the necessary conditions of experience, i.e. causality, substance,
etc.
My view is that the way out of this is through Friesian epistemology and "Ontological Undecidability."
Nevertheless, Kant's theory, as an approximation, is superior to any that have
come since -- let alone the dismal exercises in nihilism, scientism, and
scholasticism that are now so popular.
Analytic and Synthetic:
Kant and the Problem of First Principles
Three Points in Kant's
Theory of Space and Time
Kant's First Antinomy, of
Space and Time
Kantian Quantum
Mechanics
Intuition and Mysticism
in Kantian Philosophy
Metaphysics
History of Philosophy
Home Page
Intuition and Mysticism
in Kantian Philosophy
While Kant's term "intellectual intuition" is thrown around rather casually
in post-Kantian philosophy, the usage rarely conforms to Kant's meaning. Kant
contrasts "intellectual" with "sensible" intuition (Anschauung) on the
basis of the active or passive role of the object. Thus, while objects are
presented to a (passive) sensible intuition, objects are created
by an (active) intellectual intuition. To Kant himself, this meant that only God
would have an intellectual intuition. In the history of philosophy, the "active
intellect" of Aristotle and Neoplatonism may be the
antecedent of the idea of intellectual intuition, though this would tend to blur
the difference between the self and God, since it looks like there is only one
active intellect -- which was precisely the point for a system of mysticism like
Neoplatonism.
Kant, of course, had no interest in mysticism, famously pillorying the
Swedish spiritualist, Emanuel Swedenborg ("Dreams of a Visionary, Explained by
Dreams of Metaphysics," 1766), but it is important to note what mysticism would
be in Kantian philosophy. Any kind of mysticism is going 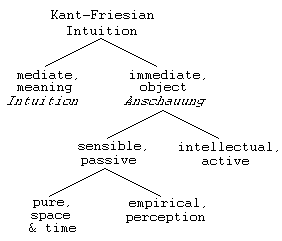 to be a kind of immediate knowledge
that is an intuitive understanding, i.e. the opposite of a discursive
understanding, where an intuitive understanding is immediate and
unarticulated, while a discursive understanding is mediate and articulated.
There is going to be no intuitive understanding in Kantian
philosophy -- i.e. no understanding that stands on its own as
knowledge, an understanding that is a ground for substantive
truths. An intuitive understanding which is not
knowledge is the common and essential experience of insight which is ordinarily
and non-technically called "intuition," e.g. "My intuition is that murder is
wrong" (in German, Nelson called it
Intuition in contrast to Kantian Anschauung). This kind of
"intuition" is not evidentiary, i.e. it doesn't prove anything. In
Socratic/Platonic terms, it is only opinion. It can only be justified
when analyzed, reduced to discursive understanding, and grounded accordingly [note]. Were ordinary
"intuitions" evidentiary, and so items of knowledge (Erkenntnisse,
cognitions), then this would be "intuitionism," the theory that knowledge
is grounded by such intuitions [note]. The self-evidence of
Aristotelian first principles
is a theory of this kind, with the proviso that intuitive self-evidence
follows, rather than precedes, discursive understanding. Other forms of
intuitionism may claim intuitive understanding prior to discursive, if
the latter is considered even possible.
to be a kind of immediate knowledge
that is an intuitive understanding, i.e. the opposite of a discursive
understanding, where an intuitive understanding is immediate and
unarticulated, while a discursive understanding is mediate and articulated.
There is going to be no intuitive understanding in Kantian
philosophy -- i.e. no understanding that stands on its own as
knowledge, an understanding that is a ground for substantive
truths. An intuitive understanding which is not
knowledge is the common and essential experience of insight which is ordinarily
and non-technically called "intuition," e.g. "My intuition is that murder is
wrong" (in German, Nelson called it
Intuition in contrast to Kantian Anschauung). This kind of
"intuition" is not evidentiary, i.e. it doesn't prove anything. In
Socratic/Platonic terms, it is only opinion. It can only be justified
when analyzed, reduced to discursive understanding, and grounded accordingly [note]. Were ordinary
"intuitions" evidentiary, and so items of knowledge (Erkenntnisse,
cognitions), then this would be "intuitionism," the theory that knowledge
is grounded by such intuitions [note]. The self-evidence of
Aristotelian first principles
is a theory of this kind, with the proviso that intuitive self-evidence
follows, rather than precedes, discursive understanding. Other forms of
intuitionism may claim intuitive understanding prior to discursive, if
the latter is considered even possible.
While mysticism is a form of intuitionism, not all intuitionism is mysticism.
The difference, again, will be in the objects. Mysticism is intuitive knowledge
of transcendent concrete objects, i.e. not the phenomenal or material concrete
objects of ordinary perception. The mystic sees things that are not part of
ordinary experience. In Kantian terms, transcendent objects cannot be
understood because they cannot be consistently articulated. For Kant, a
theory of transcendent objects ("dialectic") generates antinomies. If a Kantian theory
allowed for mystical knowledge, it would have to be unanalyzable,
unrenderable into a system of discursive understanding of transcendent objects.
This is rather like what many mystics say, since they gain knowledge which is
ineffable and inexpressible. On the other hand, mystics also claim to
intuitively derive knowledge which is analyzable and expressible,
although only intuitively justified, since, for instance, al-Ghazzali
(1059-1111) finds specific justification of Islâm and its doctrines through
mystical insight.
The intuitive apprehension of abstract objects does not rise to the
level of mysticism, since abstract objects do not have independent existence --
except when substantialized in Platonism, a theory rarely followed since.
Intuitions of abstract objects concern meaning, and in general the
ordinary sense of "intuition" (Intuition) applies to this. Such
intuitions, when analyzed, are the basis of analytic truths, but whether the
meanings apply to existence is a separate question (pace St. Anslem and
Descartes), which
requires an evidentiary basis. The mystical claim would have to be that
an intuitively apprehended abstract object is also intuitively
known to apply to existence, in a way, analyzable (as in Anselm's
"ontological argument") or unanalyzable, that transcends ordinary perception and
experience.
An important distinction in mystical claims will be between objects which are
independent and which are identical to the subject of mystical
knowledge. 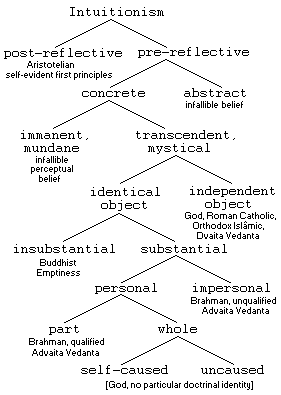 This itself is an
analyzable characteristic of mystical intuition. In monotheistic religions, God
will tend to be seen as independent. This was not an open question, and the
Christian mystic always ran the risk that contrary truths learned through
mystical intuition might conflict with Orthodoxy -- but the Catholic Church
never denied that such an avenue of knowledge existed, as with St. Teresa of
Ávila (1515-1582). Other mystics, however, paid the price of their
experiences at the stake. In Judaism and Islâm, with looser institutional
authority over doctrine, the drift of claims towards extinction of self and
identity with God is conspicious. Some efforts were made in Islâm to suppress
this, like the execution of al-H.allâj (in 922), but the precedent was
powerful. An artifact of this in Judaism remained with the philosopher Spinoza, whose sense of
identity with God is crystal clear, but who cannot properly be considered a
mystic, since his God is not transcendent, but immanent, identical with all the
objects of perception, and who does not claim intuitive knowledge beyond the
minimal Aristotelian claims about first principles. Nevertheless, Spinoza
retains a strong mystical affect, the "intellectual love of God," which
helps explain the meaning to him of a system that otherwise is rationalistic and
seems devoid of religious appeal.
This itself is an
analyzable characteristic of mystical intuition. In monotheistic religions, God
will tend to be seen as independent. This was not an open question, and the
Christian mystic always ran the risk that contrary truths learned through
mystical intuition might conflict with Orthodoxy -- but the Catholic Church
never denied that such an avenue of knowledge existed, as with St. Teresa of
Ávila (1515-1582). Other mystics, however, paid the price of their
experiences at the stake. In Judaism and Islâm, with looser institutional
authority over doctrine, the drift of claims towards extinction of self and
identity with God is conspicious. Some efforts were made in Islâm to suppress
this, like the execution of al-H.allâj (in 922), but the precedent was
powerful. An artifact of this in Judaism remained with the philosopher Spinoza, whose sense of
identity with God is crystal clear, but who cannot properly be considered a
mystic, since his God is not transcendent, but immanent, identical with all the
objects of perception, and who does not claim intuitive knowledge beyond the
minimal Aristotelian claims about first principles. Nevertheless, Spinoza
retains a strong mystical affect, the "intellectual love of God," which
helps explain the meaning to him of a system that otherwise is rationalistic and
seems devoid of religious appeal.
The distinction between independent and identical objects can be seen to
overlap Kant's between intellectual and sensible intuition. Only a sensible
intuition could relate one to an independent transcendent object, since such a
thing clearly cannot be created by one's knowing it. However, if the mystic is
identical to the transcendent object, this could allow for an intellectual
intuition, depending on the metaphysics of the object. It is possible for God's
existence to be presented to him passively, in which case he would have sensible
knowledge of himself; or, God may actually create his own existence, like that
of anything else, merely by knowing it. This fits Spinoza's priniciple of a
substance, namely God (Spinoza's only substance), being self-caused.
There, if the mystic is identical to God, who also creates everything else
through intellectual intuition, all mystical knowledge will be of the nature of
an intellectual intuition.
This is even simpler in Buddhism, where there are no substances and, at least
in some forms of Buddhist
philosophy (e.g. Yogacara), all things are clearly created by Mind.
In Pure Land Buddhism, an
important meditative practice is the visualization of the Pure Land of
the Buddha Amitabha. It is always possible to interpret this as unrelated to the
independent, or even real, existence of the Pure Land, but the metaphysics
clearly allows that the Pure Land is actually created by the act of
visualization, since all things are Mind dependent. This would be an
intellectual intuition in a strong Kantian sense, and a form of mysticism, with
the transcendence of the Pure Land, in which the identity with the mystical
object is facilitated by the absence of any substantial independence of things
whatsoever. Similarly, the Tibetan "Book of the Dead" urges the deceased to
realize that the visions of the hereafter are not independent but created by
their own Mind. Thus lies the path to Enlightenment and Salvation.
In light of this examination, we should revisit the charge of mysticism against Rudolf Otto. Since Otto does not
claim intuitive knowledge of transcendent objects, he clearly is not a mystic.
The natures of transcendent objects, to the extent that they can be theorized at
all, are matters of rational Kant-Friesian metaphysics (after the fashion
of Kant's "postulates of practical reason," which resolve some antinomies); and
Kant-Friesian metaphysics tends to dismiss more substantive doctrine from
historic religions (e.g. the Trinity, transsubstantiation, etc.). Otto's famous
theory of "numinosity" is about a property, and so an abstraction, whose
existence is certified by its presence in the objects of experience, but which
in an important way is not a natural property, since it is invisible to
science and is unrelated to mundane utility. The numinosity of God is natural to
Otto, but his God comes from the Kantian Ideas, besides historic religions, and
divine numinosity derives from no more than a phenomenology of such religions.
So is there mysticism? Of course, there actually are mystics, most of whom
are clearly sincere and deeply moved or transformed by their experiences. But
there is no philosophical mysticism in the sense that philosophy could,
as the Neoplatonists believed, certify, verify, and theorize the results of
mystical intuitions. Given a Kantian epistemology and metaphysics, no rational
or intelligible system can be built from mystical intuitions, analyzable or
unanalyzable. This, however, should be no more than what we would expect given
the contradictory claims of mystical or dogmatic authorities in world religions.
The antinomical choices between mystical intuitions as intellectual or sensible,
of independent or identical objects, of a divine substance (personal or
impersonal) or ultimate Emptiness, cannot be resolved on the evidence of
mystical knowledge, since the knowledge of different mystics confirms each of
these and, as Hume would say, the evidence of one tends to refute the evidence
of the other. This in itself is one of the most important features of human
existence, since it leaves us without any rational certainty that there
are transcendent objects at all. The mystic may just be hallucinating (or
lying), whether beholding the Virgin Mary or visualizing the Buddha Land. As
considered elsewhere, however,
this simply leaves us faced with the choices of the right and the good without
any confidence in the ulterior considerations of reward and punishment. Behind
our veil of ignorance, it is character and benevolence that are proven.
Faith, Works, and Knowledge
Analytic and Synthetic:
Kant and the Problem of First Principles
Epistemology
Philosophy of Religion
History of Philosophy
Home Page
Intuition and Mysticism in Kantian Philosophy, Note 1
Problems of justification are covered elsewhere. In Kant's theory,
complications arise over Kant's original, "architectonic," conception of
intuition (Anschauung) because, as considered in the main essay on Kant, perception itself comes to be
seen (in the Transcendental Deduction) as a product of mental activity. If
perception is itself active and intellectual, then the simple distinction
between sensible and intellectual intuition, or even between intuition and
thought, becomes confused. Friesians like Nelson don't deal with his very well
and tend to take over Kant's own naive version of the theory.
However, as is examined in detail in The Origin of Value in a Transcendent
Function ("Intuition and the
Immanent Object), 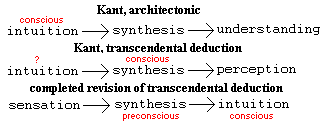 the
immediacy of intuition that is lost when we consider perception to be the result
of active mental synthesis returns when we realize that this synthesis is
an activity that cannot occur in the conscious mind. Perception is spontaneously
produced by a preconscious activity; and even if it is governed by Kant's
"pure concepts of the understanding" as rules of synthesis, these concepts do
not accompany the results as conceptual or semantic content. Perception
can occur without being understood, without particular things being
seen, or without a particular recognition determined by the percept -- as
in the Gestalt tricks where different things (e.g. faces or candlesticks) can be
seen in the same shapes. The difference between conceptual meaning and
perceptual object must be maintained, even when the empiricist tabula
rasa is rejected and mental processes are allowed into the formation of
perception. It is thus possible to continue speaking of intuition pretty much as
Kant and the Friesian do, even after taking into account the way that the
Transcendental Deduction undermines Kant's original view of intuition. There is
also the ontological aspect to this, that the phenomenal objects immanent in
perception are undecidably
both real/external and subjective/internal.
the
immediacy of intuition that is lost when we consider perception to be the result
of active mental synthesis returns when we realize that this synthesis is
an activity that cannot occur in the conscious mind. Perception is spontaneously
produced by a preconscious activity; and even if it is governed by Kant's
"pure concepts of the understanding" as rules of synthesis, these concepts do
not accompany the results as conceptual or semantic content. Perception
can occur without being understood, without particular things being
seen, or without a particular recognition determined by the percept -- as
in the Gestalt tricks where different things (e.g. faces or candlesticks) can be
seen in the same shapes. The difference between conceptual meaning and
perceptual object must be maintained, even when the empiricist tabula
rasa is rejected and mental processes are allowed into the formation of
perception. It is thus possible to continue speaking of intuition pretty much as
Kant and the Friesian do, even after taking into account the way that the
Transcendental Deduction undermines Kant's original view of intuition. There is
also the ontological aspect to this, that the phenomenal objects immanent in
perception are undecidably
both real/external and subjective/internal.
Return to text
Intuition and Mysticism in Kantian Philosophy, Note 2
In arguments about mathematics and set theory, "intuitionism" tends to mean
something else, which can be very confusing. Mathematical intuitionists don't
like mathematical or logical constructions that cannot be visualized (hence,
"intuited") and so tend to be wary or disapproving of infinities. 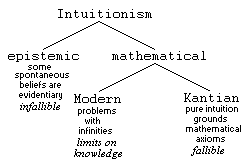 Such scruples, however, which may
be empiricist in origin, seem to have had little effect on the practice of
mathematics and, if taken seriously, would make much of modern mathematics,
including non-Euclidean
geometry, suspect. While Kant might be said to be a kind of
intuitionist in this sense, since he thinks that the axioms of geometry and
arithmetic are grounded by visualization, there is nothing to prevent the
logical extension of mathematics beyond our capacity for visualization,
which in fact is what has occurred. While Kant's mathematics is somewhat
intuitionistic in the modern mathematical sense, it is not necessarily
intuitionistic in the traditional epistemic sense, since our mathematical
"intuitions," e.g. "that looks like a triangle," can be wrong. The Kantian
mathematical intuition is much more like perception, an empirical intuition,
than it is like a true self-justifying, evidentiary intuition -- a Kantian
mathematical intuition, like an empirical intuition, can be
misunderstood, while the evidentiary intuition of (epistemic)
intuitionism is itself a kind of infallible understanding. To prevent
confusion, the mathematical sense of "intuition" and "intuitionism" is not used
in the text.
Such scruples, however, which may
be empiricist in origin, seem to have had little effect on the practice of
mathematics and, if taken seriously, would make much of modern mathematics,
including non-Euclidean
geometry, suspect. While Kant might be said to be a kind of
intuitionist in this sense, since he thinks that the axioms of geometry and
arithmetic are grounded by visualization, there is nothing to prevent the
logical extension of mathematics beyond our capacity for visualization,
which in fact is what has occurred. While Kant's mathematics is somewhat
intuitionistic in the modern mathematical sense, it is not necessarily
intuitionistic in the traditional epistemic sense, since our mathematical
"intuitions," e.g. "that looks like a triangle," can be wrong. The Kantian
mathematical intuition is much more like perception, an empirical intuition,
than it is like a true self-justifying, evidentiary intuition -- a Kantian
mathematical intuition, like an empirical intuition, can be
misunderstood, while the evidentiary intuition of (epistemic)
intuitionism is itself a kind of infallible understanding. To prevent
confusion, the mathematical sense of "intuition" and "intuitionism" is not used
in the text.
Return to text
Source: http://www.friesian.com/
 If we try to construct a square of opposition using Kant's
two distinctions, we have some trouble. A strictly constructed square of
opposition would look like the one at right. "Transcendental" (e)
is the negation of "empirical" (e), and "idealism" (r) is
the negation of "realism" (r). The structure we get, however, does not
work for Kant's theory. Transcendental idealism and empirical realism would be
contradictories and so cannot both be true, as Kant requires.
Similarly, transcendental realism and empirical idealism are also
contradictories and so cannot both be false, as Kant requires. The
features of the square of opposition that we would expect Kant's theory to
conform to would be that "contraries," the two upper members, are both false,
while the "subcontraries," the two lower members, are both true.
If we try to construct a square of opposition using Kant's
two distinctions, we have some trouble. A strictly constructed square of
opposition would look like the one at right. "Transcendental" (e)
is the negation of "empirical" (e), and "idealism" (r) is
the negation of "realism" (r). The structure we get, however, does not
work for Kant's theory. Transcendental idealism and empirical realism would be
contradictories and so cannot both be true, as Kant requires.
Similarly, transcendental realism and empirical idealism are also
contradictories and so cannot both be false, as Kant requires. The
features of the square of opposition that we would expect Kant's theory to
conform to would be that "contraries," the two upper members, are both false,
while the "subcontraries," the two lower members, are both true.

 We can then produce a square
like the one at right, which allows for the traditional truth values. In this
version the definition of "transcedental idealism" has actually been left out.
Kant's position, although terminologically embracing the two lower members, is
really well defined by only one of them, empirical realism. However, saying that
the objects of knowledge are immanent in experience and independent of
our existence involves a paradox. How can something be independent in existence
and yet dependent or immanent in our experience, our representation?
We can then produce a square
like the one at right, which allows for the traditional truth values. In this
version the definition of "transcedental idealism" has actually been left out.
Kant's position, although terminologically embracing the two lower members, is
really well defined by only one of them, empirical realism. However, saying that
the objects of knowledge are immanent in experience and independent of
our existence involves a paradox. How can something be independent in existence
and yet dependent or immanent in our experience, our representation?
 If "transcendental" means,
epistemically, "independent of experience," but "idealism" means, ontologically,
"dependent on subjective (my) existence," then "transcendental idealism" would
have to mean knowledge of objects that are dependent on my existence but
independent of my experience. This seems to be, not just a paradox, but an out
and out contradiction, since if something exists as an epiphenomenon of myself,
it hardly seems like it could be independent of my experience. Berkeley's
principle was "to be is to be perceived," but this kind of "transcendental
idealism" would require that something is because of my existence but then is
not perceived. This might work on the basis of Spinoza's metaphysics, where my
existence is God's existence, but God's knoweldge far transcends mine.
Nevertheless, since anything is God, God is part of my experience after all.
If "transcendental" means,
epistemically, "independent of experience," but "idealism" means, ontologically,
"dependent on subjective (my) existence," then "transcendental idealism" would
have to mean knowledge of objects that are dependent on my existence but
independent of my experience. This seems to be, not just a paradox, but an out
and out contradiction, since if something exists as an epiphenomenon of myself,
it hardly seems like it could be independent of my experience. Berkeley's
principle was "to be is to be perceived," but this kind of "transcendental
idealism" would require that something is because of my existence but then is
not perceived. This might work on the basis of Spinoza's metaphysics, where my
existence is God's existence, but God's knoweldge far transcends mine.
Nevertheless, since anything is God, God is part of my experience after all.
 to be a kind of immediate knowledge
that is an intuitive understanding, i.e. the opposite of a discursive
understanding, where an intuitive understanding is immediate and
unarticulated, while a discursive understanding is mediate and articulated.
There is going to be no intuitive understanding in Kantian
philosophy -- i.e. no understanding that stands on its own as
knowledge, an understanding that is a ground for substantive
truths.
to be a kind of immediate knowledge
that is an intuitive understanding, i.e. the opposite of a discursive
understanding, where an intuitive understanding is immediate and
unarticulated, while a discursive understanding is mediate and articulated.
There is going to be no intuitive understanding in Kantian
philosophy -- i.e. no understanding that stands on its own as
knowledge, an understanding that is a ground for substantive
truths.  This itself is an
analyzable characteristic of mystical intuition. In monotheistic religions, God
will tend to be seen as independent. This was not an open question, and the
Christian mystic always ran the risk that contrary truths learned through
mystical intuition might conflict with Orthodoxy -- but the Catholic Church
never denied that such an avenue of knowledge existed, as with St. Teresa of
Ávila (1515-1582). Other mystics, however, paid the price of their
experiences at the stake. In Judaism and Islâm, with looser institutional
authority over doctrine, the drift of claims towards extinction of self and
identity with God is conspicious. Some efforts were made in Islâm to suppress
this, like the execution of al-H.allâj (in 922), but the precedent was
powerful. An artifact of this in Judaism remained with the philosopher
This itself is an
analyzable characteristic of mystical intuition. In monotheistic religions, God
will tend to be seen as independent. This was not an open question, and the
Christian mystic always ran the risk that contrary truths learned through
mystical intuition might conflict with Orthodoxy -- but the Catholic Church
never denied that such an avenue of knowledge existed, as with St. Teresa of
Ávila (1515-1582). Other mystics, however, paid the price of their
experiences at the stake. In Judaism and Islâm, with looser institutional
authority over doctrine, the drift of claims towards extinction of self and
identity with God is conspicious. Some efforts were made in Islâm to suppress
this, like the execution of al-H.allâj (in 922), but the precedent was
powerful. An artifact of this in Judaism remained with the philosopher  the
immediacy of intuition that is lost when we consider perception to be the result
of active mental synthesis returns when we realize that this synthesis is
an activity that cannot occur in the conscious mind. Perception is spontaneously
produced by a preconscious activity; and even if it is governed by Kant's
"pure concepts of the understanding" as rules of synthesis, these concepts do
not accompany the results as conceptual or semantic content. Perception
can occur without being understood, without particular things being
seen, or without a particular recognition determined by the percept -- as
in the Gestalt tricks where different things (e.g. faces or candlesticks) can be
seen in the same shapes. The difference between conceptual meaning and
perceptual object must be maintained, even when the empiricist tabula
rasa is rejected and mental processes are allowed into the formation of
perception. It is thus possible to continue speaking of intuition pretty much as
Kant and the Friesian do, even after taking into account the way that the
Transcendental Deduction undermines Kant's original view of intuition. There is
also the ontological aspect to this, that the phenomenal objects immanent in
perception are
the
immediacy of intuition that is lost when we consider perception to be the result
of active mental synthesis returns when we realize that this synthesis is
an activity that cannot occur in the conscious mind. Perception is spontaneously
produced by a preconscious activity; and even if it is governed by Kant's
"pure concepts of the understanding" as rules of synthesis, these concepts do
not accompany the results as conceptual or semantic content. Perception
can occur without being understood, without particular things being
seen, or without a particular recognition determined by the percept -- as
in the Gestalt tricks where different things (e.g. faces or candlesticks) can be
seen in the same shapes. The difference between conceptual meaning and
perceptual object must be maintained, even when the empiricist tabula
rasa is rejected and mental processes are allowed into the formation of
perception. It is thus possible to continue speaking of intuition pretty much as
Kant and the Friesian do, even after taking into account the way that the
Transcendental Deduction undermines Kant's original view of intuition. There is
also the ontological aspect to this, that the phenomenal objects immanent in
perception are  Such scruples, however, which may
be empiricist in origin, seem to have had little effect on the practice of
mathematics and, if taken seriously, would make much of modern mathematics,
including
Such scruples, however, which may
be empiricist in origin, seem to have had little effect on the practice of
mathematics and, if taken seriously, would make much of modern mathematics,
including