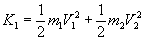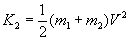Горбацевич Ф.Ф. - Гравитация и инерция

гравитация и инерция
д.т.н. Горбацевич Ф.Ф.

1. Ньютон и классическая механика

Известно сравнительно много работ, посвященных раскрытию физической сущности инерции тел [1-4]. В них излагаются историческое развитие понятия "инерция", различные виды проявления инерции тел, практическое использование инерции в работающих механизмах. Вводятся понятия инерция, инертность. Авторы некоторых работ употребляют понятия инерция и инертность, часто обозначая ими одно и то же свойство тел. Чаще всего под инерцией понимается стремление тела сохранить неизменным свое состояние по отношению к инерциальной (неподвижной) системе отсчета. Наиболее современная формулировка свойства инертности приведена в работе [5]: "всякое тело оказывает сопротивление при попытках привести его в движение или изменить модуль или направление его движения". Иначе, если на тело не действуют никакие внешние силы со стороны других тел и вообще окружающей среды, или эти силы уравновешивают друг друга, то тело сохраняет состояние покоя или равномерного прямолинейного движения. Это выражение, по сути, является первым законом Ньютона.

Как известно, первый закон Ньютона гласит: всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные к телу силы не вызовут изменение этого состояния [6]. Ньютон полагал, что в абсолютном пустом пространстве могут свободно перемещаться тела: планеты, звезды, кометы и другие части и частицы тел. В известной степени такая картина предполагает некоторую "свободу воли": тело, получив первоначальный толчок, начинает передвигаться равномерно и прямолинейно (как бы самостоятельно) в пространстве.

Опытные наблюдения показывают, что первый закон Ньютона может соблюдаться только в некоторых особых, абстрактных условиях, лишенных гравитационного поля, а также полей иного рода. Известно, что любое пространство в космосе заполнено гравитационным полем. Под воздействием гравитации траектории движения космических тел, - комет, астероидов, планет, звезд и т.п. искривляются и чаще всего приобретают эллиптические орбиты. По такой орбите Луна движется вокруг Земли. Земля и Луна обращаются вокруг Солнца. Солнце вместе с планетами солнечной системы со скоростью около 250 км/с движется вокруг центра галактики [7]. Движение небесных тел, да и земных, не может быть прямолинейным. Поэтому понятие "прямолинейное движение", "равномерное движение" можно применять только при определенных допущениях, игнорируя поля гравитации, которые пронизывают весь универсум. При практическом рассмотрении движения некоторых, например, земных тел можно считать допустимым, что тело движется прямолинейно и равномерно на определенном коротком пути, на котором искривление траектории его движения из-за влияния гравитации не очень заметно.

С другой стороны интуитивно очевидно, что если бы исчезла сила гравитации, все небесные тела – кометы, астероиды, планеты, звезды и др. начали бы двигаться равномерно и прямолинейно, то есть вдоль прямых линий в мировом пространстве. В таком гипотетическом пространстве полностью соблюдался бы первый закон Ньютона. Свободное движение по прямолинейной траектории тела изменялось бы лишь при столкновении с другим телом. Тот сгусток материи, который представляет собой физическое тело, обладает тем императивным свойством, что если он избавлен от внешних сил, оно будет сохранять прямолинейное, равномерное движение. Эта способность, обусловлена наличием у тела массы. Движущееся физическое тело, помимо массы, обладает кинетической энергией [4].

В отличие от энергии, которой обладает движущееся тело, покоящиеся тела могут обладать потенциальной энергией. При этом потенциальной энергией обладают лишь те тела, которые находятся в каком-либо градиентном силовом поле, например, в поле тяготения, а также в магнитном или других видах полей. Выше было отмечено, что все мировое пространство пронизано, наряду с другими, самым обширным и самым дальнодействующим полем гравитационных сил. Поэтому все тела, ограниченные в свободном движении, обладают потенциальной энергией. Тело может считаться покоящимся, если его потенциальная энергия не реализуется в движение. Если тело не имеет ограничивающих его движение связей с другими телами, его потенциальная энергия побуждает тело к движению и она преобразуется в кинетическую энергию.

В классической механике, развитой трудами Галилея, Ньютона, Д'Аламбера, Лагранжа, Эйлера и других, инерция физических тел рассматривается как движение материальной точки относительно системы координат, неподвижной (абсолютной) или подвижной, например, связанной с планетой Земля. В пределах подхода, использующего неподвижную систему координат, Д'Аламбер при исследовании движения несвободной точки ввел в механику вектор D, равный произведению массы m точечного тела на его ускорение a, взятое с обратным знаком [3],

D = - ma,

(1)

Этот вектор впоследствии назван даламберовой силой инерции. Эта сила, согласно третьему закону Ньютона, должна уравновешивать силу, ускоряющую тело. При таком подходе взаимодействие силы и массы тела, описываемое вторым законом Ньютона, можно свести к статической задаче. Более общий принцип, позволяющий решать сложные уравнения динамики, называется принципом Д'Аламбера—Лагранжа:
“При движении системы с идеальными связями (т. е, такими, реакции которых не могут произвести работы, — без трения, без потерь энергии и этих связях) в каждый данный момент времени сумма элементарных работ всех приложенных активных сил (т. е. не реакций) и всех сил инерции на любом возможном перемещении системы будет равна нулю” [4].
Этот принцип позволяет составить уравнения движения любой механической системы и найти те силы, которые действуют внутри системы.

Для подвижной системы координат относительно некой "абсолютной", великим Эйлером предложены дополнительные силы инерции, - переносная P и кориолисовая Q [3]. Полное уравнение динамики точечного тела с учетом этих сил инерции принимает вид

ma = F + P + Q ,

(2)

где F – действующая физическая сила.

Толкование понятия “сила” в настоящее время не является однозначным. Как считается в механике [3], уравнение (2) имеет структуру исходного уравнения абсолютного движения, в котором члены P и Q имеют размерность силы. Однако, по мнению автора работы [3], никакого механического воздействия тел эти члены не представляют, а потому физическими силами никак не являются. Считается, что это силы инерции. Cила - это векторная мера механического проявления взаимодействия тел. Время от времени среди специалистов классической механики возникают споры, являются ли силы P и Q реальными или нет. Такие же сомнения возникают относительно даламберовой силы D. Действительно, эти силы являются, скорее всего, реакциями тела на стремление изменить его состояние в соответствии с первым законом Ньютона. Такие силы считаются силами инерции. Силы, проявляющиеся при механическом контакте тел, предлагается называть физическими силами.

По нашему мнению следует сформулировать некоторое общее толкование понятия "инерция". Такое толкование или определение может быть найдено при анализе ситуаций, где инерция непосредственно проявляется при взаимодействии тел.

Проще всего рассмотреть инерцию и энергию двух сталкивающихся тел. Известно, что инерция тела пропорциональна его массе. Инерция тела существенно возрастает при увеличении скорости тела. Рассмотрим абсолютно неупругий удар на примере столкновения шаров [5]. Пусть шары движутся вдоль прямой, соединяющей их центры, со скоростями V₁и V₂. В этом случае считают, что удар является центральным. Обозначим через V общую скорость шаров после столкновения. Кинетические энергии системы до удара К₁ и после удара К₂ будут равны соответственно

, ,

(3)

где m₁ и m₂- массы шаров.

Разница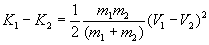 является той частью энергии, которая была поглощена при столкновении. При неупругом столкновении двух одинаковых тел, движущихся навстречу друг другу с одной и той же скоростью их взаимная скорость после столкновения равна нулю, а вся энергия тратится на разрушение тел (пример – два автомобиля). При абсолютно упругом ударе внутренняя энергия тел не меняется [5]. То есть сумма энергии каждого из тел до удара равна сумме энергии этих тел после удара.

Наиболее просто исчислить количественную характеристику инерции тела, оценивая ее изменение при столкновении малого тела с телом много большей массы М. Оценим энергию, которая будет выделена при таком столкновении. Из (3) получим, что если масса m одного из тел будет много меньше массы другого (V = V₂ = 0), выделившаяся при ударе кинетическая энергия будет равна (если пренебречь эффектами второго порядка)

, кг·м²/сек²

(4)

Эта формул впервые получена Оливером Хевисайдом и независимо от него Уильямом Томсоном [8]. Из этой формулы следует, что вся энергия при столкновении выделилась за счет малого тела. Тело массы m, двигающееся со скоростью V после столкновения с телом М будет иметь скорость V = 0. После столкновения малое тело потеряло всю инерцию по отношению к телу М. Согласно уравнению (4), его энергия движения будет равна нулю. Этот пример показывает, что инерцию тела можно приравнять к количеству кинетической энергии, запасенной в его массе и скорости движения.

Вышеизложенное позволяет заключить, что инерция или кинетическая энергия тела, может быть оценена только лишь по отношению к другому телу, относительно которого оно движется. Если не вводить какой-либо абстрактной системы координат, инерцией, как и кинетической энергией, обладает тело, которое можно считать движущимся относительно другого тела. В пределах допущения о возможности равномерного, прямолинейного движения следует понимать относительность понятий "покоящееся", "движущееся" тело. Например, тело не обладает инерцией по отношению к другому телу, относительно которого оно не движется. Когда тело покоится относительно другого тела, оно не обладает инерцией по отношению к этому другому. Можно представить два тела, движущихся в одном и том же направлении с одинаковой скоростью. Друг относительно друга они не будут обладать инерцией. Однако эти два тела будут обладать инерцией относительно третьего тела, движущегося относительно их с какой либо скоростью, отличной от нулевой.

Поэтому мера инерции (потенциальной) каждого конкретного независимо движущегося тела имеет множество значений, в зависимости от того, относительно какого другого тела оно оценивается. Инерция одного и того же тела или его кинетическая энергия будет различна по отношению к телам, движущимся с различной скоростью. Она проявляется только при столкновении с другим телом. Необходим какой-либо внешний объект, для того, чтобы оценить меру инерции или механически проявилась инерция физического тела. Поэтому этот вид инерции следует назвать внешней инерцией.

В отличие от свободного инерциального тела, движение которого (условно) можно оценить как равномерное и прямолинейное, вращающееся вокруг какой-либо оси тело обладает особым видом инерции. Можно считать этот вид внутренней инерцией тела. Внутренняя инерция, и ее оценка не зависит от внешних тел. Она имеет одно определенное значение. Внутренняя инерция и энергия вращения тела обязательно сопровождается, за счет появления центробежных сил, напряжениями и деформациями внутри тела. Внутренняя инерция сопровождается гироскопическим эффектом. Равная центробежной, центростремительная сила обеспечивает устойчивость вращения тела. Так как центростремительная сила приложена к движущемуся телу постоянно, то, согласно второму закону Ньютона считается, что тело движется ускоренно. При этом, однако, оно движется равномерно, то есть его линейная скорость каждой отдельной его точки остается постоянной. Так как это тело движется равномерно, то согласно первому закону Ньютона, можно считать, что его движение осуществляется без ускорения. Последнее утверждение, скорее всего, имеет больше оснований, поскольку при равномерном круговом движении изменений его количественных характеристик не происходит. Энергия движения и его инерция остаются постоянными.

Существует строгое соответствие между массой тела, угловой скоростью его вращения, внутренними напряжениями и деформациями. Потенциальную инерцию вращающегося тела можно численно оценить моментом инерции. Момент инерции материальной точки относительно некоторой оси равно произведению ее массы на квадрат расстояния от точки до этой оси [6]:

J = mR²

(5)

Момент инерции тела является суммой моментов инерции материальных точек, составляющих это тело. Кинетическая энергия вращающегося тела равна [6]

(6)

где ω – угловая скорость, рад.

Вращающаяся вокруг своей оси планета Земля обладает внутренней инерцией. За счет этой инерции форма геоида, в первом приближении, представляет собой приплюснутый эллипсоид, бульший радиус которого располагается в плоскости экватора. Внутренней инерцией обладает система Земля-Луна, а также Солнце-Земля, как и каждая пара звезда-планета. Внутренняя инерция тела может быть обнаружена опытным путем. Например, промеры экваториальных и полярных радиусов земного шара выявляют наличие деформации формы земли за счет ее вращения вокруг своей оси. Сила Кориолиса, (см. выражение (2)), отклоняющая направление течения рек в западном направлении в северном полушарии, а в восточном – в южном, - является свидетельством проявления внутренней инерции Земли. Маятник Фуко в закрытом помещении наглядно демонстрирует наличие этой внутренней инерции. Поскольку опытным путем в изолированном пространстве обнаруживается факт вращения тела, принцип относительности Галилея для вращающихся тел является неприменимым. Таким образом, в земных условиях принцип Галилея, строго говоря, не может соблюдаться.

Можно привести много наглядных примеров системы тел, обладающих большой внутренней инерцией. Один из них – солнечно-планетарная система. В ней движение планет осуществляется по близким к круговым, эллиптическим орбитам. Оно возможно при наличии постоянной центростремительной силы F_c, приложенной к движущемуся телу по направлению, перпендикулярном к направлению движения. При круговом движении эта сила приложена из одного, в простом случае, центра. Для того чтобы тело двигалось по круговой траектории, необходимо, чтобы эта сила была равна [6]:

, кг·м/сек²,]

(7)

где R – радиус, m – масса, V – линейная скорость движения тела по орбите.

Применительно к телу, находящемуся на земной орбите, роль силы F_c играет земное тяготение.

В пределах механики, определяемой первым и вторым законами Ньютона, следует выделить, кроме инерции, вторую характеристику, тесно с ней связанную, а именно, - инертность. Причем инертность и инерция являются разными категориями. Ряд известных работ [1-4] указывают, что мерой инертности тела является его масса. "Условно принято считать, что масса элементарной частицы определяется полями, с ней связанными, - электромагнитными, ядерными и др., однако количественной теории массы еще не создано" [4]. Различие в массах разных тел выявляется при попытке изменить их состояние, например, ускорить или замедлить, изменить направление их движения.

Меру массы тела m устанавливает второй закон Ньютона (для простоты рассмотрения, не учитываем векторный характер силы и ускорения),

F = ma,

(8)

где F - сила, побуждающее тело изменить его состояние, a - ускорение, которое приобретает тело. Из второго закона Ньютона можно увидеть, что при одной и той же силе F ускорение, которое получит тело, будет тем меньше, чем больше масса m.

Инертность присуща каждому телу, обладающему массой. Инертность – это свойство физических тел оказывать сопротивление при попытках привести его в движение, изменить модуль или направление этого движения. Таким образом, инертность свойственна и покоящимся телам. Инертность, как и масса, определяет способность тела свободно двигаться в свободном пространстве. Согласно второму закону Ньютона категории инертности и массы означают одно и то же свойство физических тел. В связи с этим, категорию "инертность" можно вполне определенно считать синонимом категории "масса".

Итак, как было указано выше, в отличие от инертности, инерция тела связана с его движением. Имеются две основные разновидности инерции: внешняя и внутренняя. Внешняя инерция представляет собой инерцию тела, движущегося (в пределах некоторых допущений) равномерно и прямолинейно. Инерция движущегося тела ничем не проявляет себя до момента столкновения с другим телом.

Внутренняя инерция присуща вращающимся телам. В отличие от внешней инерции, тела, обладающего внутренней инерцией, испытывают внутренние деформации и напряжения. Если лишить вращающееся тело внешних связей, оно будет вращаться неограниченно долго, сохраняя одну и ту же энергию вращения.

Эти понятия, внутренняя инерция и внешняя инерция в той или иной форме известны давно. Еще Галилей разделял эти виды инерции. В иных формулировках их можно трактовать как “вращательную” и “линейную” инерции. По нашему мнению, четкое разделение видов инерции на внутреннюю и внешнюю, акцент на отличие инерции и инертности будет способствовать лучшему пониманию сущности этих очень важных физических категорий. С другой стороны равенство инертности и массы тела давно признается в классической механике [3]. Подробный разбор этих понятий, выполненный выше, по нашему мнению необходим для более четкого понимания их физической сути.

На основе вышеизложенного можно отметить, что первый закон Ньютона характеризует покой и движение свободного тела, обладающего только, в пределах наших определений, внешней инерцией. Для характеристики второй, внутренней инерции он непригоден. В связи с этим, возникает потребность в формулировке объединяющего закона, который бы характеризовал оба вида инерции. По нашему мнению, эта формулировка выглядит следующим образом: "тело, приведенное в движение и свободное от внешних связей, будет двигаться неограниченно долго, полностью сохраняя энергию движения". Эта формулировка закона объединяет обе формы инерции. Она более полная и ее можно назвать законом инерции.

2. О связи инертности и гравитации

Рассмотрим еще один аспект, связанный с инертностью и массой тел. В механике Ньютона уже давно осуждается проблема отличия гравитирующей и инертной масс. Некоторые физики считают, что эти массы могут отличаться. Выполнено очень много тонких и весьма точных экспериментов с целью нахождения разницы между гравитирующей и инертной массами [9, 10]. Пока такой разницы не обнаружено [5]. На основе подхода, развитого выше, можно утверждать, что этой разницы и не должно существовать, так как инертность и масса являются адекватными категориями.

Представим себе, что на какую-либо инертную массу, путем контакта с другим телом, действует сила F_t. Тогда тело, согласно второму закону Ньютона (8) приобретает ускорение a, величина которого обратно пропорциональна массе тела m. Гравитационное поле действует на массу m также как некая сила F_g. Эта сила возникает потому, что гравитационное поле (Земли, Солнца, межгалактическое и др.) градиентно [11]. В свободном пространстве гравитационная сила вызывает ускорение тела m, величина которого будет обратно пропорциональна массе тела. И в случае ускорения силой F_t и в случае ускорения тела гравитационной силой F_gодной и той же массы m переменными могут быть силы и ускорение тела, но не ее масса. Известные опыты физика Этвеша доказывает лишь то, что любые по физическим свойствам и массе тела движутся в гравитационном поле одинаковым образом [12]. Таким образом, инертная и гравитационная массы равны, так как основа ее одна и та же – инертность тела или иначе – стремление тела сохранять свое состояние при попытках изменить это состояние.

Вместе с этим, особенности приложения силы при ускорении тела в гравитационном поле и при ускорении через контакт с другим телом, существенно отличаются. Как было выше сказано, каждое неподвижное (например, лежащее на опоре) тело в гравитационном поле обладает потенциальной энергией. Покоящееся в гравитационном поле тело испытывает внутренние нагрузки и деформации.

Чтобы это показать, разделим покоящееся на опоре тело на ряд частей. Те части, которые лежат ближе к опоре, испытывают бульшие нагрузки, чем вышележащие части, за счет давления на них вышележащих частей (нагрузка на наши ноги больше той, которую испытывают плечи). Подошвы ног испытывают давление, равное весу тела. Ощущение давления в нашем теле и есть ощущение весомости. Внутренние нагрузки и внутренние деформации возникают и в теле, которое ускоряется какой-либо силой. Можно также разделить такое тело на ряд частей. Окажется, что наибольшие внутренние нагрузки и деформации в теле испытывают те его части, которые расположены вблизи точки (поверхности), где приложена сила, ускоряющее тело. В таких телах силы (и гравитации и ускорения) приложены локально, т.е. в точке, плоскости или поверхности.

Представим свободно движущуюся замкнутую капсулу (лифт), в которой находится какое-либо физическое тело. Исчезает или уменьшается внутри такой капсулы поле тяготения? Вероятно, такое бы случилось, если бы капсула двигалась быстрее, чем скорость распространения такого поля. Как показывает опыт, гравитация практически не экранируется другими (не слишком массивными) телами. Поэтому градиентное поле гравитации будет одинаково ускорять тело, находящееся в капсуле и саму капсулу. Великий Галилей первым показал, что легкие и тяжелые тела падают в поле земного тяготения с одинаковым ускорением. Наиболее нагляден опыт, в котором демонстрируется падение в вакуумированной стеклянной трубке свинцовой дробинки и птичьего пера. Отчетливо видно, что оба предмета падают с одинаковым ускорением. Если начать делить какое-либо тело на части и наблюдать за падением этих частей в вакууме, можно заметить, что как большие части, так и малые, будут падать в поле земного тяготения с одинаковым ускорением. Продолжая подобное деление вплоть до атомов можно получить тот же результат. Отсюда следует, что гравитационное поле приложено к каждому, имеющему массу элементу, составляющему физическое тело. Оно будет одинаково ускорять большие и малые тела только в том случае, если поле является градиентным и действует на каждую элементарную частицу тел.

Гравитационное поле действительно является градиентным, причем действие силы на элементарную частицу можно сравнить с давлением жидкости на погруженное в нее тело [13]. Подобная трактовка позволяет объяснить состояние “невесомости”, которое испытывает свободно падающее тело. В классической механике следующим образом трактуется ощущении невесомости [3]. “Что такое невесомость и как ее следует понимать с точки зрения механики? Отметим прежде всего, следующее. Нервная система человека доставляет мозгу информацию о том, как одна часть тела давит на другую….” “Если же поверхностных сил нет, например, если мы предоставлены сами себе во время падения с высоты до раскрытия парашюта (сопротивлением воздуха пренебрегаем) тогда давление одной части тела да другую отсутствует, и возникает ощущении невесомости.”

В свободном падении физическое тело начинает двигаться в направлении убывания градиента поля. Если разделить подобное тело на ряд отдельных частей (частиц), то окажется, что к каждой из этих частей приложено одинаковое градиентное давление (если пренебречь изменением градиента в пределах длины такого тела). Выше мы показали, что как большие, так и малые (и сверхмалые) тела одинаково ускоряются в гравитационном поле. Отсюда следует, что гравитационное давление распределено таким образом, что оно приложено к каждому атому (в том числе, его ядру, электронам) составляющем тело. Гравитационное давление не приложено к телу в целом, в какой-либо точке или поверхности, оно распределено и действует внутри тела. Каждое из этих частей, каждый атом получает одинаковое ускорение в гравитационном поле. Поскольку получаемые ускорения составляющих тело частей (частиц) одинаковы, между ними отсутствуют напряжения и деформации, и реализуется то состояние, которое называют невесомостью. Невесомость и есть то состояние, когда в теле между его частями отсутствуют внутренние напряжения (если например, не рассматривать длинный стержень, ориентированный в направлении градиента силы тяжести).

Заметим, что, в отличие от тела, покоящегося на опоре и находящегося в гравитационном поле, сила гравитации в свободном от внешних связей теле не приложена локально, а оказывает свое действие одинаково на каждую частицу, составляющую тело. В этом состоянии гравитация ответственна за ускорение, увеличение скорости движения тела в свободном движении к центру тяготения. Если сила, которая приложена к телу через точку или поверхность контакта - это векторная мера механического проявления взаимодействия тел, то сила гравитации, - это распределенное градиентное давление на каждую элементарную частицу, составляющее тело.

Итак, действие гравитации, осуществляется благодаря тому, что гравитационное поле является градиентным и его градиент приложен не к какой-либо одной точке тела, его части или к телу в целом, но к каждой элементарной частице, составляющей это тело. Однако, для того, чтобы существовало градиентное поле, передающее свое градиентное давление на каждую элементарную частицу, должна существовать среда, свободно проникающая во все физические тела без исключения. Только в этом случае будет соблюден принцип близкодействия. Такой средой, свободно проникающей во все физические тела и осуществляющей градиентное давление гравитации, является эфир, или эфирная среда [11]. Действие гравитации через эфирную среду не исчезает ни в теле, лежащим неподвижно на опоре ни в том, которое находится в свободном падении. Градиентное давление эфирной среды в теле, находящемся неподвижно на опоре, действует через силы на каждую элементарную частицу. Эти силы складываются в сумму давления тела на опору, называемого нами весом тела. Внутри тела возникают деформации, тем большие, чем ближе к опоре.

При свободном падении тела градиентное давление эфирной среды распределено внутри тела. Оно действует на каждую элементарную частицу внутри тела и остается тем же по величине, что и в неподвижном теле. Образование градиентного давления эфира возникает потому, что размеры частиц эфира, по оценке, много меньше элементарных частиц, образующих физические тела. Анализируя эффективную поляризуемость частиц эфира, А.А. Потапов [14] пришел к выводу, что их размер равен планковской длине:

a = l_p =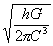 = ~ 1·10^-32мм,

где h – постоянная Планка, G – гравитационная постоянная, С – скорость света.

Этот размер на много порядков меньше размеров элементарных частиц. Как известно, размеры атомов, включая их электронные оболочки, составляют доли и единицы ангстрем, то есть ~(1-10)Ч 10^-10 м. Размеры ядер имеет порядок ~10^-14 м. Радиус электрона (классический) составляет 2,818Ч 10^-15 м [15]. Размеры других элементарных частиц не очень существенно отличаются от размера электрона и могут быть меньше не более, чем на два порядка. Сравнение размеров частицы эфира (~ 1·10^-35 м), ядер и электрона показывает, что частицы эфира легко могут проникать и размещаться между атомами, во внутриатомном пространстве. Проникновение света в прозрачные тела (длина волны, например, видимого света, составляет (4-7)10^-7 м [16]) подтверждает одинаковость основы, которая колеблется при возбуждении ее квантами света, как в пустоте, так и внутри тел [17]. Физическое тело, состоящее из ядер атомов и электронов, представляет собой как бы пространственную “решетку”, внутри которой находится эфир. Его градиентное давление на ядра и электроны, составляющие эту “решетку” приводит к появлению силы гравитации.

Из вышеприведенного следует, что эфирная среда является существенным субъектом классической механики и не может из нее исключена. Наличие эфирной среды позволяет объяснить природу тяготения [13]. Вместе с этим имеются концепции, отрицающие существование эфирной среды. В настоящее время предлагается много десятков версий теории гравитации [18]. Одна из самых известных излагается в общей теории относительности (ОТО). Согласно этой теории имеется соответствие между гравитацией и инерцией. Это соответствие объясняется тем, что тяготение и инерция кажутся одним и тем же потому, что они являются одним и тем же [19]. В ОТО такое соответствие называется принципом эквивалентности. Согласно письму А. Эйнштейна Э. Маху принцип эквивалентности состоит в эквивалентности ускоренной системы и гравитационного поля ([19], стр. 169). Иными словами, по этой теории, в лифте, движущемся в космосе с ускорением, в точности равным ускорению падающего на землю тела, действительно будет искусственно создаваться сила, равная силе земного притяжения. Естественно, что этот воображаемый космос должен быть лишен гравитационного поля.

Сравнительно легко можно показать, что существует принципиальная разница в состоянии тела, находящемся в гравитационном поле с гравитационной постоянной G и тела, ускоряемого с тем же ускорением F = G. Составим тело, состоящее из двух масс, объединенных вместе стержнями, как это показано на рис. 1a. В горизонтальный стержень встроим динамометр D₁. Составим второе тело, которое будет устроено аналогично первому, с динамометром D₂, рис. 1b. Первое тело ускоряется ускорением F, равным G в пространстве, лишенном способности проявлять силы тяготения. Второе тело находится в устойчивом равновесии в гравитационном поле с ускорением G. Нетрудно заметить, что показания динамометра D₁на теле рис. 1а будут больше, чем динамометр D₂на теле 1b, так как массы тела рис.1b будут притягиваться друг к другу. Этот пример ясно показывает несостоятельность принципа эквивалентности.

Рис. 1. Схема, поясняющая различие в состоянии тела, находящегося неподвижно в поле тяготения (а) и тела, ускоряемого физической силой (b).

Однако этот пример лишь демонстрирует верность второго закона Ньютона. При такой имитации тяготения в теле, которое находится в лифте, движущемся вверх, распределенное гравитационное поле отсутствует.

При помощи нашей концепции градиентного гравитационного поля легко пояснить механизм образования состояния невесомости внутри спутника, движущегося по околоземной орбите. Применительно к телу, находящемуся на земной орбите, роль силы F_c (уравнение (7)) играет земное тяготение. В этом случае F_c = mg, где g – ускорение силы тяжести. Средняя величина земного ускорения g = 9.81 м/сек².Подставив величину центростремительной силы, которая обеспечивает величина земного тяготения в формулу (7), получим, что на круговой орбите вокруг Земли (исключая влияние формы Земли, влияния Луны, Солнца и др.).

g = V²/R.

(9)

В этом случае центростремительная сила, обусловленная земным тяготением, будет уравновешена центробежной силой инерции F_c, аналогичной переносной силе Р Эйлера. Центробежная сила – F_c, также как и гравитационная сила действует распределено и одинаково на каждую часть, частицу, каждый атом орбитального физического тела, уравновешивая гравитационную. В этом и состоит причина невесомости тел, находящихся на земной орбите. Заметим, что согласно уравнению (9) все тела, вне зависимости от их массы, достигшие круговой скорости V, будут становиться "невесомыми".

В итоге отметим, что именно то, что гравитационная сила, представляющая собой градиентное давление на каждую элементарную частицу, которые составляют физическое тело, приводит к наблюдаемому факту, что все тела падают с одинаковым ускорением. Этот факт впервые установил великий Галилео Галилей. Принятие положения о том, что гравитация является распределенным градиентным давлением решает проблему одинаковости гравитирующей и инертной масс.

Вышеприведенные аргументы демонстрируют то поразительное обстоятельство, что некоторые проблемы не только небесной, но и классической механики невозможно решить без концепции эфира. Здесь уместно процитировать механика А. Ишлинского [3]: “Реальны или нереальны силы инерции? Сторонники реальности сил инерции приводят в доказательство факты возникновения натяжения веревочки при вращении на ней камешка, разрыва быстровращающихся маховиков, ощущения дополнительной тяжести при разгоне лифта вверх и др. Они утверждают, что мы не смогли бы отличить силы инерции от “реальных” сил, если бы вечно находились в подземелье и не знали ни о вращении Земли вокруг своей оси, ни о ее движении вокруг Солнца. И пришли ли бы мы вообще в этом случае к обычным законам механики Галилея - Ньютона и т.д. Можно привести многочисленный перечень подобных примеров и вопросов”. Как показано выше, принятие концепции эфирной среды позволяет снять существующие противоречия.

3. Взаимодействие масс с гравитацией и эфиром

В общей оценке инерционного движения следует учитывать, что все тела движутся в эфире или иначе, в эфирной среде [11]. Причем это относится как космическим телам, так и к микрочастицам. Вышеописанная оценка инерции тел относится к величинам скорости движения, которые заведомо много ниже скорости распространения электромагнитных волн (света) в эфире С. Тело, движущееся в эфирной среде со скоростью, много меньшей скорости света, практически не взаимодействует с эфирной средой [15]. Физическое тело, равномерно движущееся в эфирной среде, не испытывает сопротивления. Эфир по своим свойствам напоминает идеальную среду не проявляющую эффекты трения. На возможность тела сохранять бесконечно долго прямолинейное и равномерное движение в идеальной жидкости, совсем не испытывая сопротивления, указывал еще Д’Аламбер [2]. Но в тоже время, эфир имеет определенные характеристики как у специфического твердого тела [11].

Раскрытие особенностей и свойств эфирной среды происходит в течение очень продолжительного времени. Первые предположения о существовании светоносной и всепроникающей среды были сформулированы еще в древней Греции. Ньютон считал эфир ответственным за передачу гравитационных воздействий: "полагать, что одно тело может воздействовать на другое, находящееся от него на некотором расстоянии, через вакуум без каких либо "посредников", ….- для меня настолько абсурдно, что по–моему, ни один человек, обладающий хотя бы малейшим представлением о философских материях, не может в это верить" [1]. Джеймс Клерк Максвелл выявил отличие эфира от известных сред: "Эфир отличен от обыкновенной материи. Когда свет движется через воздух, то очевидно, что среда, по которой свет распространяется, не есть сам воздух, потому, что, во-первых воздух не может передавать поперечных колебаний, а продольные колебания, им передаваемые, распространяются почти в миллион раз медленнее света" ...."С какими бы трудностями в наших попытках выработать состоятельное представление о строении эфира ни приходилось нам сталкиваться, но несомненно, что межпланетное и межзвездное пространство не суть пространства пустые, но занятые материальной субстанцией или телом, самым обширным и, надо думать, самым однородным, какое только нам известно" [20].

В дальнейшем, открытие Г. Герцем электромагнитных волн сообщили несколько новых важных свойств эфиру. Помимо передачи гравитационных воздействий, влияния статических электрических зарядов, силу магнитов, эфир способен передавать электромагнитные волны. Он обладает диэлектрической и магнитной проницаемостями, волновым сопротивлением, специфической плотностью. Солнечный свет оказался набором электромагнитных волн. Инфракрасные и ультрафиолетовые лучи, жесткое рентгеновское излучение переносит тот же носитель – эфир или иначе эфирная среда.

Сравнительно недавно по результатам наблюдений системы Земля-геостационарный спутник подтверждено, что скорость распространения электромагнитных колебаний в свободном пространстве определяется только и только свойствами эфирной среды [21]. С какой бы скоростью не передвигался бы источник, скорость распространения от него электромагнитных волн равна скорости света в эфире. При этом обнаружено влияние движения Земли на аберрацию электромагнитных волн от источника, установленного на спутнике. Это дало возможность измерить параметры абсолютного движения Земли и Солнечной системы без применения астрономических наблюдений за звездами. Полученные значения орбитальной компоненты скорости Земли (29,4 км/с), прямого восхождения апекса Солнца (270^о) и его склонения (89.5^о), а также скорости абсолютного движения Солнечной системы согласуются с известными в наблюдательной астрономии. Такой результат является прямым доказательством того, что скорость равномерно движущейся лабораторной системы координат (в нашем случае Земли) реально может быть измерена при помощи устройства, в котором источник излучения (геостационарный спутник) и приемник (антенна наземного телескопа) находятся в состоянии покоя относительно друг друга и этой же системы координат. Это говорит о том, что эфирная среда в межзвездном пространстве может быть принята в качестве независимой системы координат.

Наиболее зримо взаимодействие движущегося с околосветовой скоростью физического тела (частицы) проявляется при явлении, носящем название эффекта Черенкова. Впервые этот эффект был зарегистрирован в прозрачной воде, окружающей радиоактивные материалы, излучающие высокоэнергичные частицы. Эффект заключается в излучении квантов света частицами, если частица, например, электрон движется со скоростью V, превышающей фазовую скорость V_f света в этой среде. При этом соблюдается условие [22]

(10)

где С - скорость света в вакууме (эфирной среде), n – коэффициент преломления на частоте ω. Этот эффект состоит в том, что частица излучает свет в пределах определенного конуса рассеивания. Угол конуса θ определяется отношением скорости фазовой скорости света в среде и движения заряженной частицы в ней.

(11)

Соотношения (10, 11) были получены на основе аналогий с эффектами, возникающими при движении тел в газах при скорости, близкой к скорости звука в газе. О том, что такие аналогии полезны, указывает В.Л. Гинзбург [22]: "В развитии физики и (трудно в этом сомневаться) других наук большую роль имеют аналогии, перенос представлений из одной области в другую. Поэтому для плодотворной работы в науке очень важно обладать широким горизонтом, а не ограничиваться, как это нередко бывает, лишь узкой специализацией". Конус возникающего излучения (11) аналогичен конусу Маха, ограничивающему фонт ударной волны, в газовой среде (воздухе) при движении какого-либо тела со сверхзвуковой скоростью. Возникновение ударной волны в газе происходит при превышении скорости движения тела скорости звука, то есть при соблюдении условия (10).

Эффект Черенкова зарегистрирован в прозрачных средах, в которых скорость распространения электромагнитных волн ниже скорости этих волн в эфире. Имеются работы, в которых экспериментально зарегистрировано движение частиц со сверхсветовыми скоростями [23]. В экспериментах производились наблюдения черенковского излучения при движении пучка ионов свинца. При этом обнаружено превышение движения этих частиц свыше скорости света на (1.00006-1.0047)С. Известна работа А. Зоммерфельда, в которой рассмотрено движение заряда в вакууме (то есть в эфире) со сверхсветовой скоростью [24]. Им был получен результат, что такой заряд должен излучать.

Итак, частица, двигающаяся с околосветовой скоростью излучает. Это означает, что она теряет энергию движения и инерцию. Таким образом, путь такой частицы со сверхсветовой скоростью конечен. Помимо этого масса движущейся частицы (тела) зависит от величины скорости, если эта скорость приближается к скорости света, то есть к той скорости, с какой распространяются в эфире электромагнитные колебания. Многочисленные эксперименты показывают, что масса тела зависит от скорости его движения в эфирной среде. Эта зависимость выражается формулой [19]:

(12)

где m₀ -масса частицы покоя, m - масса частицы в движении относительно эфирной среды, V - скорость движения частицы, С - скорость света.

Зависимость (12) показывает, что при приближении скорости частицы к скорости света происходят явления, схожие с явлениями, наблюдаемыми при приближении скорости тела к скорости звука в газах. Здесь также полезно применить метод аналогий, на который указывал В.Л. Гинзбург. Однако существует принципиальная разница между этими явлениями. При движении тела в газе, газ обтекает его. При движении тела в эфирной среде, эфирная среда движется сквозь физическое тело [11]. При этом эфирная среда непосредственно взаимодействует с каждой элементарной частицей, составляющей физическое тело и имеющей массу, - с электронами, протонами, нейтронами и др.

При приближении скорости движения частицы к скорости света, ее масса становится равной m. Если замедлить такую частицу, ее скорость снова становится равной m₀ – то есть массе покоя. Скорее всего это означает, что масса самой частицы, вне от величины ее скорости в эфире равна m₀. Дополнительной массой, равной m_е = m - m₀ является присоединенная масса эфира.

Формула (12) позволяет заключить, что движение относительно эфирной среды возможно со сколь угодно малой разницей между V и C. Однако это движение не может долгое время происходить со скоростью V = C, так как при этом энергия и масса частицы станет бесконечно большой. Законы сохранения массы-энергии налагают запрет на бесконечно большие массы любых тел. Из этого можно сделать вывод, что физические тела не могут продолжительное время двигаться сквозь эфирную среду со скоростью света.

Последний вывод имеет важное следствие, - фотоны, кванты света, которые всегда распространяются со скоростью C, не могут иметь массы, а, следовательно, являются волнами, возмущающими эфирную среду и распространяющимися в ней. Как известно, фотоны (кванты) обладают широким спектром различающихся частот, от теплового диапазона до рентгеновских лучей. Бесконечное число фотонов (квантов) разных частот распространяются в эфире по всем направлениям и воспринимаются приборами как электромагнитные волны, свет, рентгеновское излучение.

* * *

В заключение, суммируя некоторые результаты, отметим отличия инерции (кинетической энергии) тел, движущихся со скоростями много ниже скорости света (малыми скоростями) и с околосветовыми скоростями. Для тел, движущихся с малыми скоростями можно заметить, что тело не обладает инерцией по отношению к другому телу, относительно которого оно не движется. Инерция одного тела по отношению к другому тем выше, чем больше его масса и скорость. Инерция тела будет различна по отношению к другим телам, движущимся с различающимися скоростями. Поэтому инерция движения каждого конкретного тела имеет множество значений, в зависимости от того, относительно какого другого тела оно оценивается.

При движении тел (частиц) с околосветовыми скоростями законы Ньютона нарушаются. Происходит взаимодействие движущихся тел с эфиром. Их инерция существенно возрастает. Также как и при движении с малыми скоростями, инерция тела может быть оценена относительно другого тела. Однако при движении с околосветовыми скоростями инерция тела может быть оценена и относительно самой эфирной среды. По нашему мнению, при околосветовой скорости движения происходит присоединение части увлекаемой массы эфира к массе тела. Движение тел в эфире не может долго происходить со скоростью, равной скорости распространения электромагнитных волн в эфире, так как при этом инерция, энергия и масса частицы станет бесконечно большой.

В итоге отметим, что разделение понятий, связанных с массой (инертность) и движением физического тела (инерция) делает эти фундаментальные категории более понятными и объяснимыми. Исчезает так называемая "загадка сил инерции". С этих позиций принцип Маха [25]: "сила инерции любого тела обусловлена его гравитационным взаимодействием со всеми удаленными массами вселенной" также подлежит критике. Ввиду изменчивости оценки силы инерции, в том числе и космических тел, относительно каждого другого, этот принцип становится не очевиден. Вместе с этим, ввиду эквивалентности понятий "инертность и "масса" и определенных свойств эфира следует утверждать, что сила гравитации в любой конкретной точки вселенной определяется всеми, содержащимися в универсуме космическими массами, включающими все видимые и невидимые ее формы, где бы они не находились. С позиции теории эфирной среды последнее утверждение достоверно. Эфирная среда передает гравитационное воздействие (как и другие виды полей) от одного физического тела к другому. Каждое физическое тело искажает эфирную среду, находящуюся в ее окрестности. Сила притяжения убывает обратно пропорционально квадрату расстояния от тела сферической формы. Оно быстро ослабевает с расстоянием. В тоже время, Благодаря эфирной среде эта сила не прекращает своего действия ни на каком, даже астономически большом расстоянии.

Литература

1. Newton. Mathematical principles of natural philosophy. Optics. Britannica, V. 32. Second Edition. Chicago. 1994.

2. Даламбер Жан Ле Рон. Динамика. Новокузнецк: ИО НФМИ, 2000, 336 с.

3. Ишлинский А. Ю. Механика относительного движения и силы инерции. М.: Наука, 1981. 320 с.

4. Гулиа Н.В. Инерция. М.: Наука, 1982. 152 с.

5. Сивухин Д.В. Общий курс физики. Т1. Механика. М.: ФИЗМАТЛИТ. 2006. 560 с.

6. Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике - М.: Наука, 1974. – 255 с.

7. Куликова В.В., Куликов В.С., Бычкова Я.В., Бычков А.Ю. История Земли в галактических и солнечных циклах. Петрозаводск: КарНЦ РАН, 2005, 250 с.

8. Thomson W. (Lord Kelvin) Mathemathical and Physical Papers. Vol. III, Art. XCIX(49), C (50), CII (52). London, Cambridge University Press, 1890. 529 p.

9. Roll P.G., Krotkov R., Dicke R.H. Ann. Phys. 26, 442, 1964.

10. Брагинский В.Б. Физические эксперименты с пробными телами. М.: Наука. 1970. 136 с.

11. Горбацевич Ф.Ф. Основы теории непустого эфира. - Апатиты: Изд. МИЛОРИ. 1998. - 48 с.

12. Грушинский Н.П., Грушинскийй А.Н. В мире сил тяготения. М.: Недра, 1978, 175 с.

13. Горбацевич Ф.Ф. О силе тяготения. В кн.: Пространство, время, тяготение. Материалы IX Международной научной конференции 7-11 августа 2006, г. С.-Петербург. СПб: "ТЕССА", 2007. С. 86-97.

14. Потапов А.А. Деформационная поляризация: Поиск оптимальных моделей. – Новосибирск, Наука, 2004. 511 с.

15. Эберт Г. Краткий справочник по физике. - М.: Физматгиз, 1963. 552 с.

16. Борн М., Вольф Э. Основы оптики. - М.: Наука, 1970. - 855 c.

17. Горбацевич Ф.Ф. Эфирная среда и универсум. Санкт-Петербург: АЛЬФА-ШТАМП, 2004. 112 с.

18. Иваненко Д.Д., Сарданашвили Г.А. Гравитация. М.: Едиториал УРСС, 2004. 200 с.

19. У.И. Франкфурт. Специальная и общая теория относительности. - М.: Наука, 1968. 331 с.

20. Максвелл Д.К. Статьи и речи. - М.: Наука, 1968. – 422 c.

21. Штырков Е.И. Обнаружение влияния движения Земли на аберрацию электромагнитных волн от геостационарного спутника – новая проверка специальной теории относительности. В кн.: Пространство, время, тяготение. Материалы IX Международной научной конференции 7-11 августа 2006, г. С.-Петербург. СПб: "ТЕССА", 2007. С. 297-310.

22. Гинзбург В.Л. Излучение равномерно движущихся источников (эффект Вавилова-Черенкова, переходное излучение и некоторые другие явления). Акустический журнал, Т. 51, № 1, 2005. С. 24-36.

23. Тяпкин А.А. Экспериментальные указания о существовании тахионов, полученные при исследовании черенковского излучения.

24. Sommerfeld A. Gottingen Nachrichten (1904) s. 9, 363; Gottingen Nachrichten (1905) s. 201. (Ссылки приведены из работы [22]).

25. Мах Э. Механика. Историко-критический очерк ее развития. — Ижевск: Ижевская республиканская типография. 2000. 456 стр.

к оглавлению