Die Gravitationserscheinungen zeigen die einzigen an getrennten Kцrpern bestehenden Wirkungen, fьr die man noch keinen Anteil des zwischenliegenden Raumes, d. h. kein Vorhandensein sich von Ort zu Ort mitteilender Verдnderungen in ihm nachweisen kann. Um so begreiflicher ist die Hoffnung, dass es schliesslich einmal gelingen werde, den fehlenden Nachweis zu fьhren. Nur darf man die Sache nicht so betrachten, wie wenn an der Scheinbarkeit jener Ausnahme nicht zu zweifeln sei. Alle bekannten und verstandenen Beobachtungen drдngen vielmehr zum Gegenteil. Es muss daher, falls dies dennoch bloss auf mangelnder Erfahrung oder unvollstдndiger Analyse beruht, erst dargethan werden, dass es Thatsachen giebt, die unsere bisherige Auffassung nach entgegengesetzter Seite berichtigen und ergдnzen. Dazu ist es vor allem nцtig, jede Hypothese fern zu halten, die mehr annimmt, als dass in dem Rдume zwischen zwei gravitierenden Massen etwas geschehe, das teil an der Gravitation hat. Wegen frьherer дhnlicher, doch unzureichender Behandlungen der hier erцrterten Frage sei auf das der 69. Naturforscherversammlung erstattete Referat ьber Fernwirkungen von Drude verwiesen.

Zwei gravitierende Massen geben sich als solche durch den Widerstand zu erkennen, den sie einer Vergrцsserung ihres Abstandes entgegensetzen. Damit mьssen also, wдhrend sie selbst in Ruhe oder in Bewegung sein kцnnen, die etwa vorhandenen Vorgдnge in dem Rдume zwischen ihnen zusammenhдngen. Offenbar ist mit der Lage oder mit ihr und dem momentanen Bewegungszustande der Massen, soweit дussere Einflьsse ausgeschlossen sind, nicht nur der eine, цrtliche Widerstand, sondern auch die Reihe aller bis ins Unendliche folgenden Widerstдnde bestimmt. Die zu ihrer Ьberwindung notwendige Arbeit ist also ebenso wie der einzelne Widerstand selbst eine die Gravitation

charakterisierende GrцЯe. Bloss sie kann hier, wo es darauf ankommt, ob mit der Gravitation sich im Rдume unter Zeitverlust ausbreitende Verдnderungen verbunden sind, als Grundgrцsse angesehen werden. Denn es hat dem Begriffe nach keinen Sinn, von der rдumlichen Fortpflanzung des Widerstandes oder der Anziehung zu reden, da Widerstand und Anziehung als solche nur an den Orten vorhanden sind, wo sich die Massen befinden. Aber wenn von einem Vorgange ausgesagt wird, er brauche Zeit, um von einem nach einem anderen Ort zu gelangen, so heisst dies, er hцrt an dem ersten Orte zu existieren auf, ohne in demselben Augenblick sogleich an dem zweiten Orte zu sein; daher wьrde die in dem Vorgange enthaltene Energie zeitweise verschwinden, wenn sie nicht durch die zwischen den beiden Orten gelegenen Punkte hindurchginge. Sie ist gleich der genannten Arbeit, sobald der Vorgang zur Gravitation zweier in den Orten befindlichen Massen gehцrt, da er dann ebenfalls von deren Lage und momentanem Bewegungszustande abhдngt und diese nicht zwei verschiedene Energiegrцssen bedingen kцnnen.

Nun werde, indem zur Unterscheidung die eine Masse die anziehende, die andere die angezogene heisse, unter dem Potential V der anziehenden Masse auf die angezogene m der auf die Einheit der zweiten Masse entfallende Teil der Arbeit verstanden, die zu leisten ist, damit sich die Massen bis ins Unendliche von einander entfernen, die mithin insgesamt Vm betrage. Fьr den Punkt, in dem sich die festgehalten gedachte Masse m befindet, und dessen Koordinaten, bezogen auf die ebenfalls festgehaltene anziehende Masse, x, y, z seien, kann man nach der in M a c h s Prinzipien der Wдrmelehre beschriebenen Methode V berechnen, indem man es gleich dem Mittelwert aller in nдchster Umgebung des Punktes herrschenden Potentiale setzt. V ist ja keine gerichtete Grosse und fьr eine gegebene Lage unverдnderlich in der Zeit. Es sei in m gleich f(x, y, z} und fьr einen Nachbarpunkt gleich

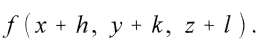
Ferner bedeute

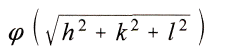
das Gewicht des Nachbarpunktes im Mittelwert, das bei Nahwirkungen mit wachsender Entfernung schnell abnimmt. Dann findet man

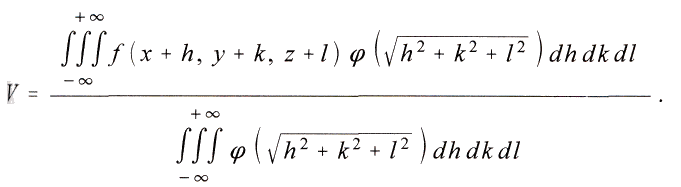
Entwickelt man f nach der Taylor sehen Reihe bis zur zweiten Potenz, und integriert man um den Punkt x, y, z herum, so wird

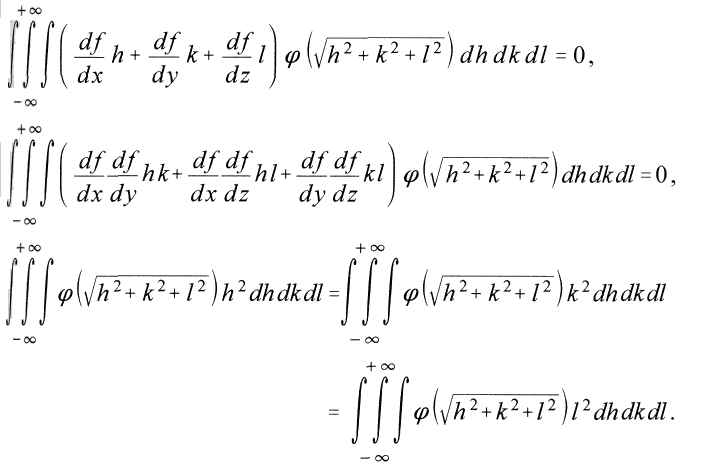
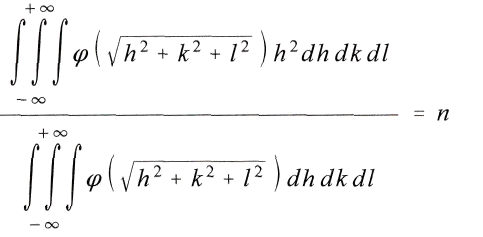
setzt,

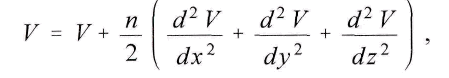
also

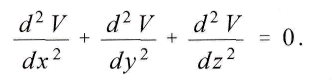
Aus dieser Gleichung folgt auf bekannte Weise, wenn /u eine Konstante bezeichnet und r der Abstand der Massen ist,

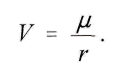
Hieraus ergiebt sich das N e w t o n sehe Gravitationsgesetz. Denn

loslдsst. Die Zunahme von Vm stimmt mit der erscheinenden lebendigen Kraft dT ьberein, und darum enthдlt T in jenem Augenblick ebenso wenig wie V die Дnderung von r in der Zeit. Folglich hat man nach den allgemeinen Lagrange sehen Bewegungsgleichungen, indem man an Stelle der дusseren auf die Masse m wirkenden Kraft den negativen Wert der von ihr ausgeьbten Kraft setzt, fьr die Beschleunigung von m

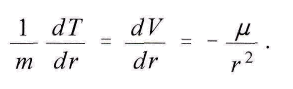
Das Newton sehe Gesetz schreibt die Potentiale vor, die die Massen in jeder Lage erreichen, wenn ihnen die zu deren Zustandekommen erforderliche Zeit zur Verfьgung steht. Diese Bedingung ist immer erfьllt, sobald die Massen in ihrer gegenseitigen Entfernung festgehalten werden. Sie hцrt auf bei eingetretener freier, einander entgegen gerichteter Bewegung, falls jene Zeit eine endlich bemessene Grosse hat. Zwei Umstдnde sind dabei von Einfluss. Erstens muss

zwar im Abstдnde r - Ar der Massen, wo Ar bei wachsendem r positiv, bei abnehmendem negativ ist, das Potential sich in der im umgekehrten Verhдltnis zu r - Ar stehenden Grosse zu bilden anfangen, weil sonst nicht einzusehen wдre, wie sich dieses Verhдltnis bei der Ruhe der Massen zu erfьllen vermцchte. Aber es gelangt nicht sogleich zur Wirkung an m, da der es bedingende Vorgang von der anziehenden Masse ausgeht und Zeit braucht, um bis zur angezogenen Masse fortzuschreiten. Selbstverstдndlich findet ein Fortschreiten der gedachten Art auch von der angezogenen zur anziehenden Masse statt, дhnlich wie zu jeder Wдrmeausstrahlung zwischen zwei Kцrpern eine Gegenstrahlung gehцrt. Das bei dem Abstдnde r - Ar von der anziehenden Masse ausgehende Potential bethдtigt sich also in m erst zu einer um A t spдteren Zeit, nachdem der Abstand gleich r geworden ist. Zweitens wьrde das Potential wohl bei Fernwirkung unmittelbar in seinem vollen Betrage erscheinen; sind jedoch Raum und Zeit in der vorausgesetzten Art mit im Spiel, so hat es auch eine gewisse Dauer nцtig, damit es, bei m angelangt, dieser Masse sich mitteile, d. h. den ihm entsprechenden Bewegungszustand von m hervorrufe. Denn nur die Annahme von Fernwirkungen lдsst Unstetigkeit in den Erscheinungen zu; ihre Ersetzung durch die Annahme von Nahwirkungen hat vor allem den Zweck, die sich an den ьbrigen physikalischen und chemischen Verдnderungen bewдhrende Stetigkeit auch in die Auffassung der Gravitation einzufьhren. Wie sich daher beim Stosse die Stosskraft aus succ. Elementarstцssen zusammensetzt, so geschieht die Ьbertragung des als Potential anlangenden Vorganges auf m durch schnell aufeinander folgende Differentialpotentiale. Wenn die Massen ruhen, geht die Bewegung des Potentials mit ihrer eigenen Geschwindigkeit an m vorьber; dann bemisst sich sein auf m ьbertragener Wert nach dem umgekehrten Verhдltnis zum Abstдnde. Wenn die Massen aufeinander zueilen, verringert sich die Zeit der Ьbertragung, mithin der ьbertragene Potentialwert im Verhдltnis der eigenen Geschwindigkeit des Potentials zu der aus ihr und der Geschwindigkeit der Massen bestehenden Summe, da das Potential in Bezug auf m diese Gesamtgeschwindigkeit hat.

Das Potential bewegt sich ausser mit seiner Geschwindigkeit c noch mit der Geschwindigkeit der anziehenden Masse, von der es ausgeht. Der Weg r – Δr, den die beiden sich entgegenkommenden Bewegungen, die des Potentials und die der angezogenen Masse, in der Zeit A t zurьcklegen, betrдgt daher

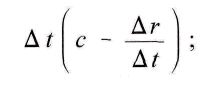
wдhrend r = c Ar ist. Also erhдlt man fьr den Abstand, bei dem sich das Potential zu bilden anfдngt, und dem es umgekehrt proportional ist,

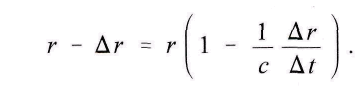
Weil ferner die Geschwindigkeit, mit der die Bewegungen an einander vorbeigehen, den Wert

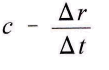
hat, fällt das Potential wegen des Zeitverbrauches zu seiner Mitteilung an m auch proportional

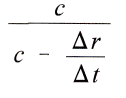
aus. Man findet so

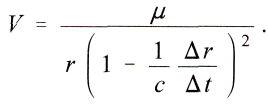
Solange der Weg dr kurz und deshalb dr/dt gegen c klein ist, darf

man dafьr dr/dt setzen. Dadurch wird

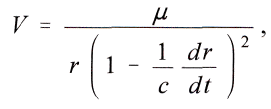
woraus mit Hülfe des binomschen Satzes bis zur zweiten Potenz folgt

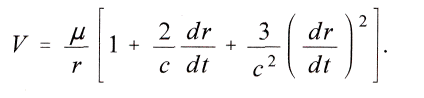
Hier ist in dem Ausdruck fьr V nicht bloss r, sondern auch die Ableitung von r nach der Zeit enthalten. Darum ergiebt sich vermцge der allgemeinen Lagrange sehen Bewegungsgleichungen fьr die

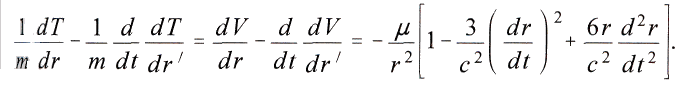
Die Annahme, dass dr/dt im Vergleich mit c klein ist, trifft im Gebiet der gewцhnlichen Gravitationserscheinungen zu; sonst kцnnte das Newton sehe Gesetz sich nicht an bewegten Massen in dem MaЯe bewahrheiten, wie es dies thut. Aber unter besonderen Bedingungen, z. B. durch eine den Massen von aussen erteilte Anfangsgeschwindigkeit, kann dr/dt so gross werden, dass weder dr/dt ihm gleich gesetzt werden darf, noch die Entwickelung der binomischen Reihe bis zur zweiten Potenz genьgt. Die abgeleitete Formel hat daher nur Gьltigkeit, wenn die gravitierenden Massen ein freies, nach aussen hin unabhдngiges System bilden. In diesem, ьbrigens vor der Hand wichtigsten Falle bestimmt sie die Verдnderung, die das Newton sehe Gesetz dadurch erleidet, dass sich die Potentiale zwischen den Massen nicht momentan, sondern mit Zeitverlust ausbreiten.

Je nachdem die Beobachtungen fьr die in die vorige Rechnung eingefьhrte Grosse c einen endlichen oder einen unendlich grossen Wert liefern, findet man mehr oder weniger sicher, dass die Potentiale gravitierender Massen Zeit brauchen, um die zwischen diesen liegenden Abstдnde zu durchschreiten, oder dass eine solche zeitliche Ausbreitung nicht existiert, mithin die Gravitation auf wahrer Fernwirkung beruht. Besonders bedarf es der Erfьllung zweier Forderungen. Erstens sind wegen des Ьbergewichtes von c ьber dr/dt

die c enthaltenden Glieder des Ausdruckes fьr die Beschleunigung der Masse m von dem ganzen Ausdrucke abzusondern und mit den Thatsachen vergleichbar zu machen; zweitens ist die Grцssenart zu ermitteln, durch die das Vorhandensein eines endlichen Wertes von c zu erkennen sein muss, und daraufhin dann die Erfahrung zu prьfen. Da der Schauplatz der Thatsachen nur das Planetensystem sein kann, stelle man sich als die anziehende Masse die Sonne, als die angezogene einen Planeten vor. Zur Vereinfachung werde dessen Bewegung auf die Sonne als Anfangspunkt der Koordinaten bezogen, sodass die Konstante mu im Verhдltnis der Summe der Massen zur anziehenden

Masse vergrцssert gedacht werden muss. Man setze

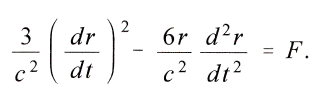
Also ist

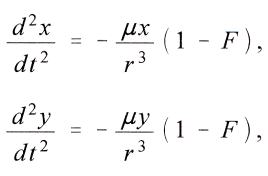
woraus durch Multiplikation der einen Gleichung mit y und der anderen mit x und durch Subtraktion folgt

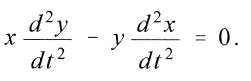
Dies ist die auch bei der Ableitung der Eigenschaften und der Bahn der Planetenbewegung aus dem Newton sehen Gesetze entstehende Gleichung, die durch Integration und Einfьhrung von Polarkoordinaten, wenn ft der Winkel zwischen dem Radiusvektor und der positiven Abscissenaxe ist und L eine Konstante bedeutet, ergiebt

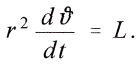
ferner

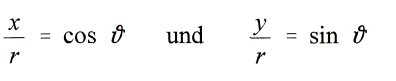
in die Gleichungen fьr

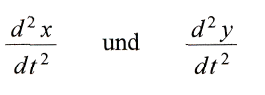
ein, so lauten diese

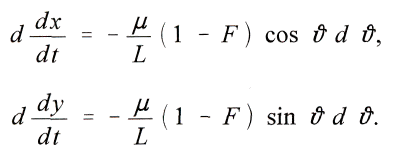
Mit den Konstanten M und N wird durch Integration

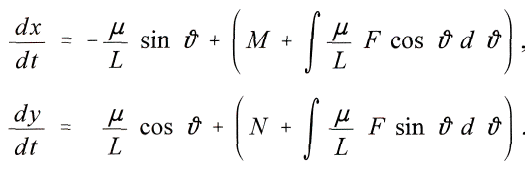
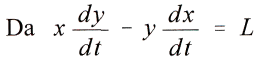
ist, findet man aus den beiden letzten Gleichungen

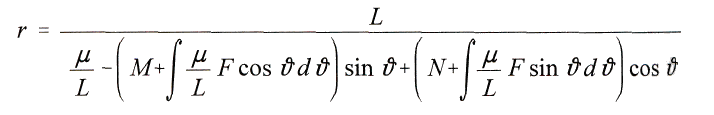
Die Integrale im Nenner nehmen nach und nach andere und andere Werte an, falls F nicht verschwindet. Setzt man voraus, man wisse ihren Wert zu einer bestimmten Zeit, so kann man sagen, dass der Planet sich zu dieser Zeit auf einer durch jene Gleichung beschriebenen Ellipse befinde. Ist deren halbe grosse Axe a, ihre halbe kleine Axe b, die numerische Exzentricitдt e und der Winkel von a mit der positiven Abscissenaxe co, und lцst man die Gleichungen fьr

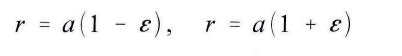
und r = b²/a nach

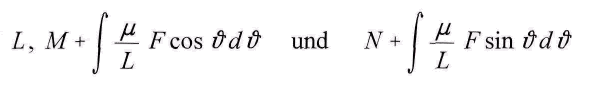
auf, so erhдlt man

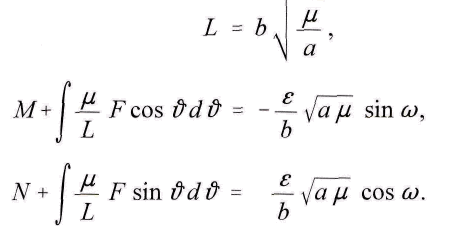
Man sieht, indem man die Unverдnderlichkeit von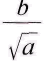beachtet, dass sich die Bewegung des Planeten so deuten lдsst, wie wenn er auf einer Ellipse einhergehe, deren e und o) sich stetig verдndern. Nur fьr den Fall, dass F = 0 ist, hцrt diese Verдnderung auf. Sie ist es also, wodurch das Vorhandensein eines endlichen Wertes von c in Wirkung kommt. Man erhдlt fьr F, sobald man die beiden letzten Gleichungen nach & differenziert, den Wert von L einsetzt und die eine durch

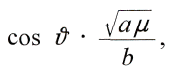
die andere durch

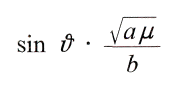
dividiert,

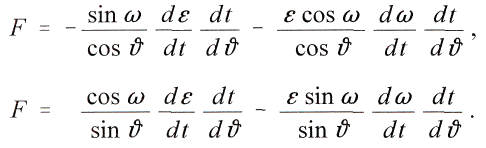
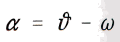
Durch Gleichsetzung beider Ausdrьcke ergiebt sich mit

woraus rückwärts folgt

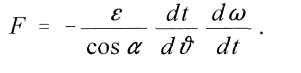
Um mittelst dieses Wertes eine nur Beobachtungsgrцssen

enthaltende Gleichung fьr 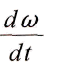zu gewinnen, stelle man F durch die

Ableitungen von r nach t dar. Man hat, wieder mit Berьcksichtigung

der Unverдnderlichkeit von 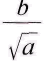ausserdem mit Benutzung der Formeln

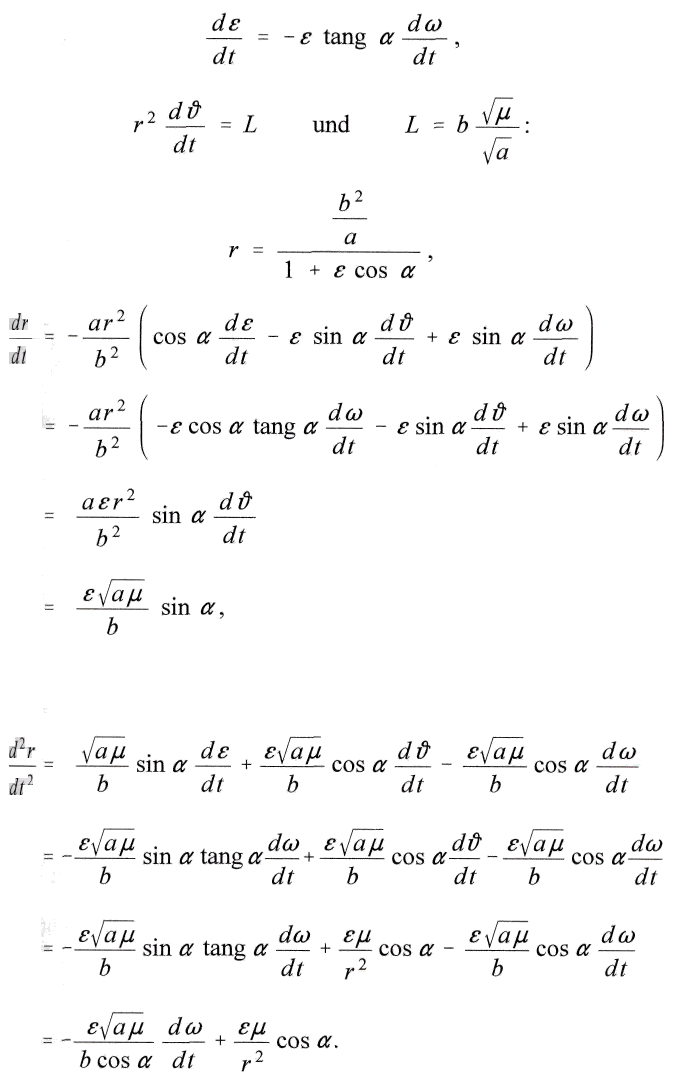
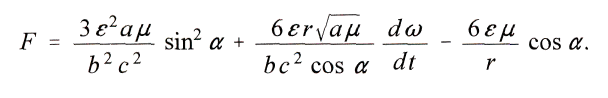
Daher lautet die gesuchte Gleichung fьr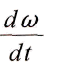

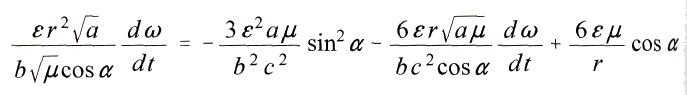
oder nach Einsetzung von

und nach Division durch

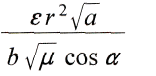
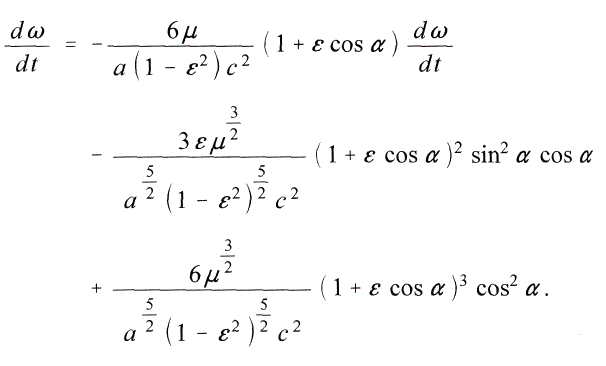
Wenn man den so berechneten Wert der Geschwindigkeit 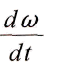mit den Beobachtungen vergleichen will, hat man zu berьcksichtigen, dass die Rechnung nur einen einzigen Planeten voraussetzt. Daher kцnnen allein Perihelbewegungen in Betracht kommen, die nicht aus Stцrungen entstehen. Solche sindbloss beim Merkur bekannt, in einem Betrage von etwa 41" in einem Jahrhundert. Diese Kleinheit schliesst von vornherein jede erfahrungsmдssige Feststellung der stetigen Verдnderlichkeit von 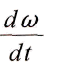aus. Also ist ьber eine lдngere Zeit hin zu integrieren. In der letzten Gleichung kommt nur e, nicht auch de/dt vor; und sofern die Дnderungen von £ gegen £ selbst verschwinden, kann man dieses als konstant ansehen. Es genьgt danach als Grenzen der Integration a = 0 und a = 2 n zu wдhlen, da bei jedem folgenden Umlauf die Werte des vorigen Umlaufes sehr annдherungsweise wiederholt.

Man multipliziere die Gleichung fьr mit dt und setze im zweiten und im dritten Gliede der rechten Seite

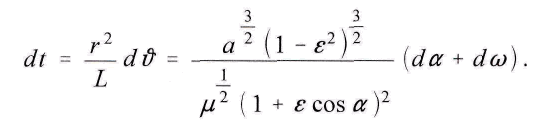
Durch passende Ordnung und Division ergiebt sich

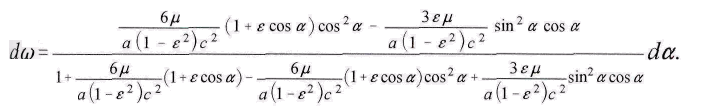
Dividiert man Zähler und Nenner durch

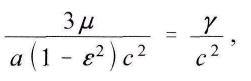
ordnet man nach steigenden Potenzen von cos a, und setzt man zur

Abkьrzung

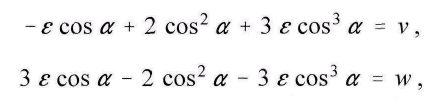
so wird

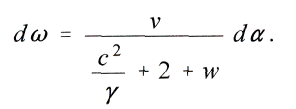
Angenдhert erhдlt man

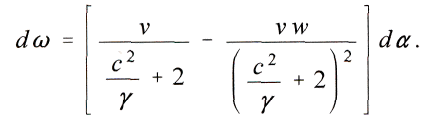
Fьr die Perihelbewegung fy wдhrend eines Umlaufes ergiebt sich daher

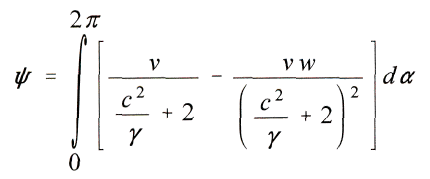
oder, weil

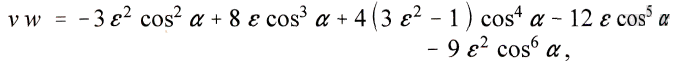
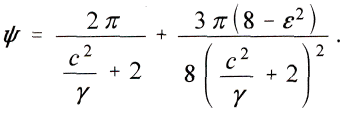
Daraus folgt

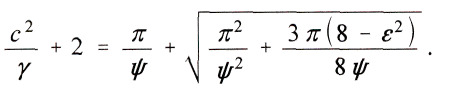
Beachtet man, dass psi sehr klein ist, so sieht man, dass das zweite

Glied unter der Wurzel gegen das erste verschwindet. Der fьr da) gewдhlte Nдherungsausdruck ist danach noch zu genau, d. h. w hдtte von vornherein vernachlдssigt werden dьrfen. Mithin wird

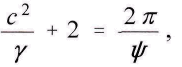
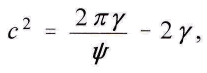
wo aus demselben Grunde 2 gamma gegen 2 pi gamma/psi unberьcksichtigt bleiben kann. Man erhдlt daher schliesslich

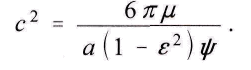
Hierin ist

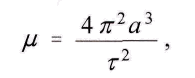
wenn r die Umlaufszeit des Planeten bedeutet. Speziell fьr Merkur gelten folgende Werte:

a = 0,3871 • 149 • 10⁶ km,

e = 0,2056,

t = 88 Tage,

psi = 4,789 • 10^-7.

Man findet damit

c = 305500 km/sec.

Die kleinste bisher gefundene Geschwindigkeit des Lichtes hat F o u c a u 11 erhalten, gleich 298000 km/sec; die grцsste ergiebt sich nach der Methode von Rцmer aus den neuesten Beobachtungen zu 308000 km/sec; die Geschwindigkeit der elektrischen Wellen fand Hertz in seinen Versuchen 320000 km/sec. Also stimmtdie Geschwindigkeit, mit der sich das Gravitationspotential ausbreitet, mit der Geschwindigkeit des Lichtes und der elektrischen Wellen ьberein. Darin liegt zugleich die Bьrgschaft, dass diese Geschwindigkeit existiert.

Freilich wird niemand in Abrede stellen, dass die Perihelbewegung des Merkur von 41" in einem Jahrhundert auch durch andere, noch unbekannte Umstдnde bedingt sein kцnnte, so dass es eine endliche Geschwindigkeit des Gravitationspotentials nicht zu geben brauchte. Man hat aber zu bedenken, dass die hier hauptsдchlich entscheidende, ьbrigens auch die Abweichung von allen frьheren Ergebnissen дhnlicher Untersuchungen bedingende Formel fьr die Abhдngigkeit des Potentials von einer solchen Geschwindigkeit auf vцllig naturmдssigem, nicht erst durch schwierige Hypothesen fьhrendem Wege gewonnen ist. Es wдre daher ein sonderbarer Zufall, wenn die 41 Sekunden des Merkur gerade die Licht- und Elektrizitдtsgeschwindigkeit lieferten, ohne mit einer rдumlich-zeitlichen Ausbreitung der Gravitation etwas zu thun zu haben, da doch das Medium, worin diese Ausbreitung und die Bewegung des Lichtes und der elektrischen Wellen erfolgen, derselbe zwischen den Weltkцrpern sich erstreckende Raum ist. Nicht einmal die verhдltnismдssig grosse Perihelbewegung, die man mit dem gefundenen Werte von c fьr die Venus erhдlt, nдmlich 8 " in einem Jahrhundert, kann als stichhaltiger Einwand gelten; oder eine Revision der Stцrungen dieses Planeten mьsste die Mцglichkeit jener Zahl endgьltig ausschliessen. Es sei daran erinnert, dass die Berechnungen der sдkularen Beschleunigung des Mondes zwischen 6" und 12" zu schwanken vermochten. Im ьbrigen ergeben sich lauter unmerklich kleine Perihelbewegungen. Sie betragen nach den aus den gebrдuchlichen Tabellen leicht zu entnehmenden Beobachtungswerten bei der Erde in einem Jahrhundert 3 ",6, beim Monde 0 ",06, beim Mars 1",3, beim Jupiter 0",06, beim Saturn 0", 01, beim Uranus 0",002 und beim Neptun 0",0007.