
 |
Пространственное и временное
распространение гравитации
Пауль Гербер
(Старгард, Померания, 1898)
перевод на русский Йохана Керна (Johann Kern) , 2004
1. Основной закон
Гравитация, согласно бытующим взглядам, проявляет себя единственно воздействием на отдельные тела, в котором ещё не видно участия расположенного между телами пространства, т.е. по нему невозможно доказать наличия проявления изменений при переходе от одной точки пространства к другой. Тем понятнее надежда, что когда-нибудь удастся получить недостающее доказательство. При этом нельзя исходить из того, что подобное исключение самого пространства в гравитации является доказанным, а не кажущимся. Все известные и понятые наблюдения вынуждают нас к противоположному выводу. Поэтому необходимо, несмотря на недостающий опыт и неполный анализ, показать, что есть факты, которые направляют наше прежнее понимание в противоположную сторону, уточняя его и дополняя. Поэтому, прежде всего, необходимо относиться с недоверием к любой гипотезе, по которой предполагается, что в пространстве между двумя гравитирующими массами не происходит ничего, что участвовало бы в гравитации. Из-за прежних подобных, однако недостаточных рассмотрений анализируемого здесь вопроса, обращаю внимание на реферат Друде, направленный 69-му Собранию исследователей природы.
Две гравитирующие массы проявляют себя как таковые через сопротивление, которое они оказывают увеличению расстояния между ними. Следовательно, поэтому возможные процессы в пространстве между ними должны быть взаимосвязаны, будут ли тела находиться в состоянии покоя или движения. Поскольку внешние воздействия исключены, то, очевидно, что положением или моментальным состоянием движения масс определено не только местное сопротивление, но и весь ряд сопротивлений, вплоть до уходящих в бесконечность. Следовательно, необходимая для их преодоления работа является, также как и само одиночное сопротивление, одной из характеризирующих гравитацию величин. Только она может рассматриваться здесь как основополагающая величина, от которой зависит, связаны ли с гравитацией распространяющиеся в пространстве изменения. Поэтому, по существу не имеет смысла вести речь о пространственном распространении сопротивления или притяжения, так как сопротивление или притяжение как таковое имеется только в месте расположения масс. Но если о процессе утверждается, что ему необходимо время, чтобы от одного места добраться до другого, то это означает, что он перестаёт существовать в прежнем месте без того, чтобы в то же самое мгновение тотчас появиться в другом, поэтому проявляющаяся в этом процессе энергия должна бы на некоторое время исчезать, если она не проходит через последовательность пунктов между указанными местами. Она равна упомянутой работе, если процесс относится к гравитации находящихся в указанных местах масс, так как он в этом случае также зависит от их положения и состояния движения в данный момент. Энергетическая величина процесса должна быть однозначной и неразрывной.
Далее для различия одна масса будет называться притягивающей, а другая притягиваемой. Под потенциалом V притягивающей массы, действующим на притягиваемую массу m, будет пониматься часть работы, действующая на единицу второй массы, которая в сумме равна Vm. Последняя должна быть равной работе, необходимой для удаления масс друг от друга на бесконечное расстояние. Для пункта, в котором находится масса, мыслимая закреплённой, и его координат применительно к также удерживаемой притягиваемой массе, потенциал
V можно вычислить по методу, описанному в Принципах учения о теплоте Маха, тем, что его принимают равным усреднённому значению всех потенциалов действующих в ближайшей окрестности точки x, y, z. Это значение не является корректной величиной, и для данного положения неизменяемой во времени.Пусть величина
V в m равна f(x, y, z), а в соседнем пункте равнаf(x + h, y + k, z + l).
Далее
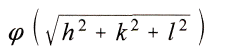
обозначает осреднённый вес соседнего пункта, который при близкодействии быстро уменьшается по мере увеличения расстояния.
Тогда можно найти
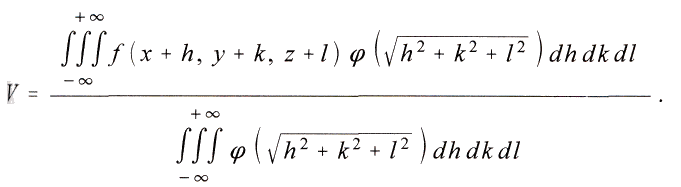
Если разложить
f в ряд Тейлора вплоть до членов второй степени и проинтегрировать вокруг точки x, y, z, то получим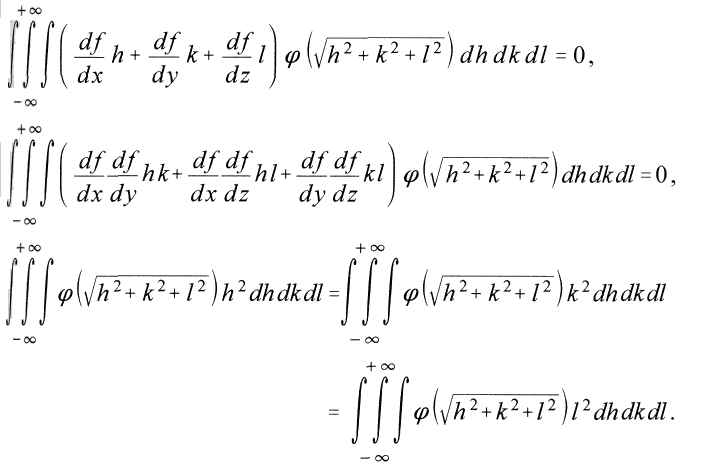
Отсюда получится
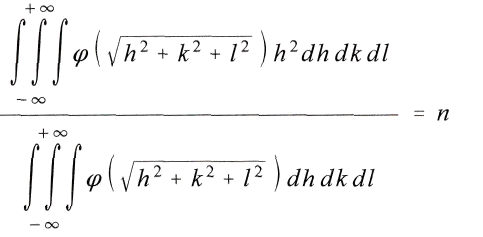
если положить
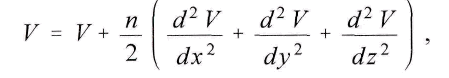
следовательно
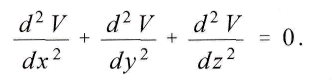
Если
μ означает константу, а r – расстояние между массами, то из этого уравнения известным образом следует, что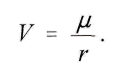 . Отсюда следует закон гравитации Ньютона. Потому что
. Отсюда следует закон гравитации Ньютона. Потому что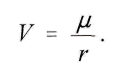 имеет силу ещё и в тот момент, когда массы свободны. Прирост величины Vm совпадает с возникающей живой силой dT, и потому T в этот момент подвергается изменению также мало, как и V от r в это же самое время. Следовательно, по общим уравнениям движения Лагранжа мы имеем следующее. Внешнюю силу, действующую на массу m, заменяют на противоположную и порождённую ей силой, создающей ускорение массы m:
имеет силу ещё и в тот момент, когда массы свободны. Прирост величины Vm совпадает с возникающей живой силой dT, и потому T в этот момент подвергается изменению также мало, как и V от r в это же самое время. Следовательно, по общим уравнениям движения Лагранжа мы имеем следующее. Внешнюю силу, действующую на массу m, заменяют на противоположную и порождённую ей силой, создающей ускорение массы m:
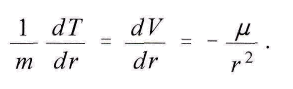
Закон Ньютона предписывает массам потенциалы, достигаемые ими в каждом положении, если у них достаточно времени для достижения этих состояний. Это условие всегда выполнимо, если массы удерживаются в их статичном положении. Оно прекращается при наступившем свободном, направленном навстречу друг другу движении. При этом надо учитывать два обстоятельства. Во-первых необходимо именно наличие расстояния
r - Δr между массами, где Δr положительно при растущем r, и отрицательно при уменьшающемся, чтобы потенциал был противоположным по отношению к величине r – Δr, потому что иначе невозможно представить, как это отношение может выполняться при покоящихся массах.Однако этот потенциал не воздействует тотчас на
m, так как приводящий к этому процесс исходит от притягивающей массы и требует времени, чтобы продвинуться к притягиваемой массе. Естественно, имеет место такого же рода продвижение со стороны притягиваемой массы к притягивающей, подобно тому, как каждому излучению тепла между двумя массами соответствует противоположное излучение. Исходящий при расстоянии r - Δr со стороны притягивающей массы потенциал воздействует на m только в момент времени на Δt более поздний того момента, когда расстояние станет равным r. Во вторых, этот потенциал при дальнодействии проявился бы непосредственно в своей полной величине. Если же сказывается влияние пространства и времени, то требуется определённое время, чтобы достигнуть массы m и передаться ей, т.е. вызвать соответствующее этому состояние движения m. Потому что только предположение дальнодействия допускает изменчивость явлений. Их замена предположением близкодействия имеет прежде всего ту цель, чтобы ввести оправдывающее само себя, как и в случае других химических и физических процессов, измеримое понимание гравитации. Поэтому, как при ударе сила удара составляется из элементарных ударов, так же происходит и перенос гравитационного потенциала процесса действующего на m и быстро следующих друг за другом дифференциальных потенциалов. При покоящихся массах перемещение потенциалов m проходит с их собственной скоростью; тогда переносимая на m величина потенциала измеряется по обратной величине расстояния меду ними. Когда массы движутся по направлению друг к другу, время переноса потенциала уменьшается, и вместе с ним уменьшается переносимый потенциал как отношение собственной скорости потенциала к сумме скоростей масс, так как потенциал по отношению к m имеет эту скорость.Кроме как со своей скоростью
c, потенциал движется ещё и со скоростью притягивающей массы, от которой он исходит. Поэтому путь r – Δr встречных движений потенциала, который притягиваемые массы проходят за время Δt равен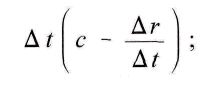
где
r = cΔt. Следовательно, для расстояния, при котором начинает появляться потенциал, можно получить, причём оно обратно пропорционально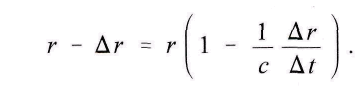
Так как далее скорость, с которой движущиеся потенциалы минуют друг друга, имеет значение
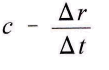
потенциал из-за расхода времени на свою передачу
m, становится пропорциональным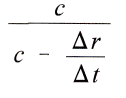
Таким образом, находим
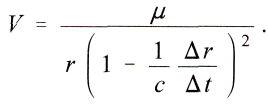
Пока путь
Δr мал, и поэтому Δr / Δt мало по сравнению с c, можно его заменить на dr/dt. Поэтому будет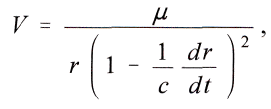
откуда с помощью биноминального разложения с сохранением членов до 2-го порядка малости следует
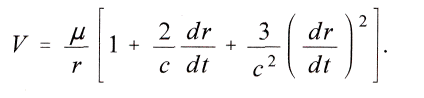
Здесь в этом выражении для
V содержится не только r, но и производная от r по времени. Поэтому благодаря общим уравнениям движения по Лагранжу для ускорения массы m получаем, если dr/dt обозначить через r΄,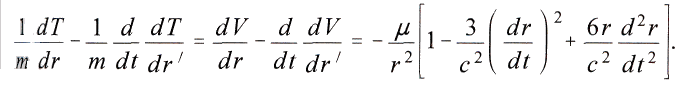
Принятое условие, что
dr/dt мало по сравнению с c, для гравитации обычно соответствует действительности; иначе закон Ньютона не был бы применим для движущихся тел, а это имеет место. Но при особенных условиях, например, при которых массам извне придана начальная скорость, dr/dt может стать настолько большим, что оно не только не может быть приравнено Δr/ Δt, но и при биноминальном разложении сохранение членов только до 2-го порядка малости будет недостаточно. Поэтому полученная формула имеет силу только в том случае, когда гравитирующие массы образуют свободную систему без внешних воздействий. В этом, по-видимому, наиважнейшем случае, она определяет изменения, которым подвергается закон Ньютона при условии, что потенциалы между массами распространяются не мгновенно, а за определённое, то есть конечное время.2. Скорость распространения
В зависимости от того, дают ли наблюдения конечную или бесконечную величину для
c в приведённых выше вычислениях, можно с большей или меньшей уверенностью утверждать, что потенциалам гравитирующих масс нужно время, чтобы пройти находящееся между ними расстояние, или что на это время не требуется, и этим гравитация базируется на настоящем дальнодействии. Особенно необходимо выполнение двух требований.Во-первых, из-за преобладания по величине
c над dr/dt, члены, содержащие c в выражении для ускорения массы, надо отделить от остального выражения, чтобы сделать возможным сравнение с фактами.Во-вторых, следует определить род величины, посредством которой может быть обнаружено наличие конечной величины
c, и после этого сравнить с опытом. Так как сценой проявления подобных фактов может быть только планетная система, нужно себе представить Солнце как притягивающую массу, а притягиваемой массой - одну из планет.Для упрощения их движение будет рассматриваться относительно Солнца, помещённого в начало координат, так что постоянная
μ в отношении сумм масс к притягиваемой массе должна представляться увеличенной.Положим
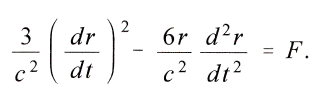
Тогда
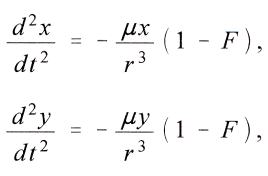
откуда после умножения одного уравнения на
x, а другого на y и последующего сложения уравнений следует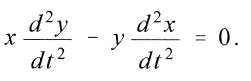
Это же уравнение получается и из закона Ньютона при исследовании свойств и траекторий движения планет, которое в случае интегрирования и введения полярных координат даёт
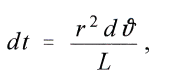
где
υ означает угол между радиусом-вектором и положительным направлением оси абсцисс , а L – постоянная.Если содержащуюся здесь величину
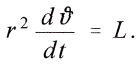
а также
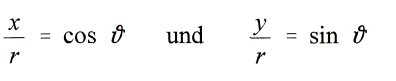
вставить в уравнения для
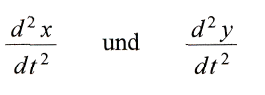
то из них получится
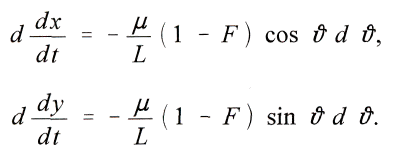
С константами
M и N получится путём интегрирования 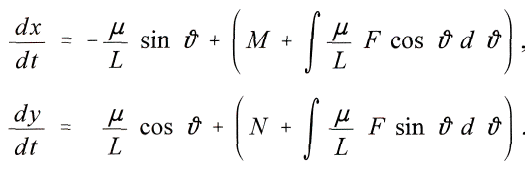
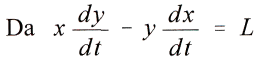
из последнего уравнения получим
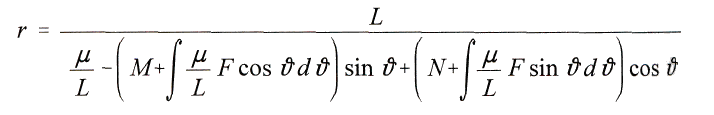
Интегралы в знаменателе последовательно принимают новые и новые значения по мере изменения
υ, если F не становится равным нулю. Если принять, что мы знаем их значения в определённый момент, то можно сказать, что планета к этому моменту находится на одном из эллипсов, описываемых этим уравнением. Если его большая полуось a, а малая полуось b, его численный эксцентриситет ε, и угол a с положительной полуосью абсцисс - ω, и решить уравнение для значений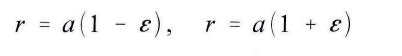
и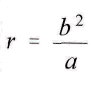 для
для
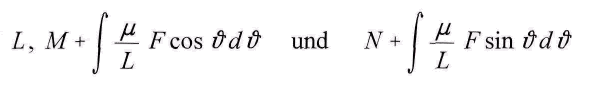
и
то мы получим
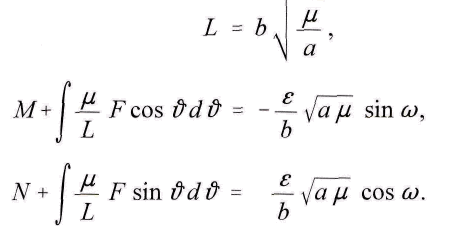
Замечая постоянство величины 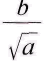 мы видим, что движение планеты можно толковать таким образом, как будто она движется по эллипсу с постоянно изменяющимися ε и ω. Только для случая, когда
мы видим, что движение планеты можно толковать таким образом, как будто она движется по эллипсу с постоянно изменяющимися ε и ω. Только для случая, когда
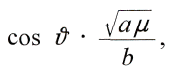
а другое на
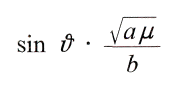
мы получим для
F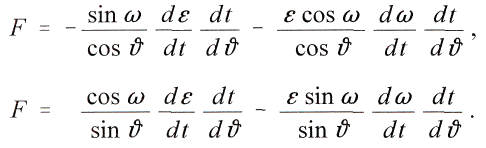
Приравнивая одно выражение другому и обозначив 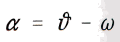
получим

и затем, возвращаясь назад
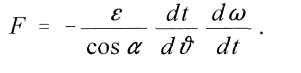
Чтобы с помощью этой величины получить уравнение для
dω/dt, содержащее только наблюдаемые при астрономических измерениях величины, надо выразить F через производные от r по t.Используя постоянство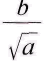 и, используя кроме того формулы
и, используя кроме того формулы
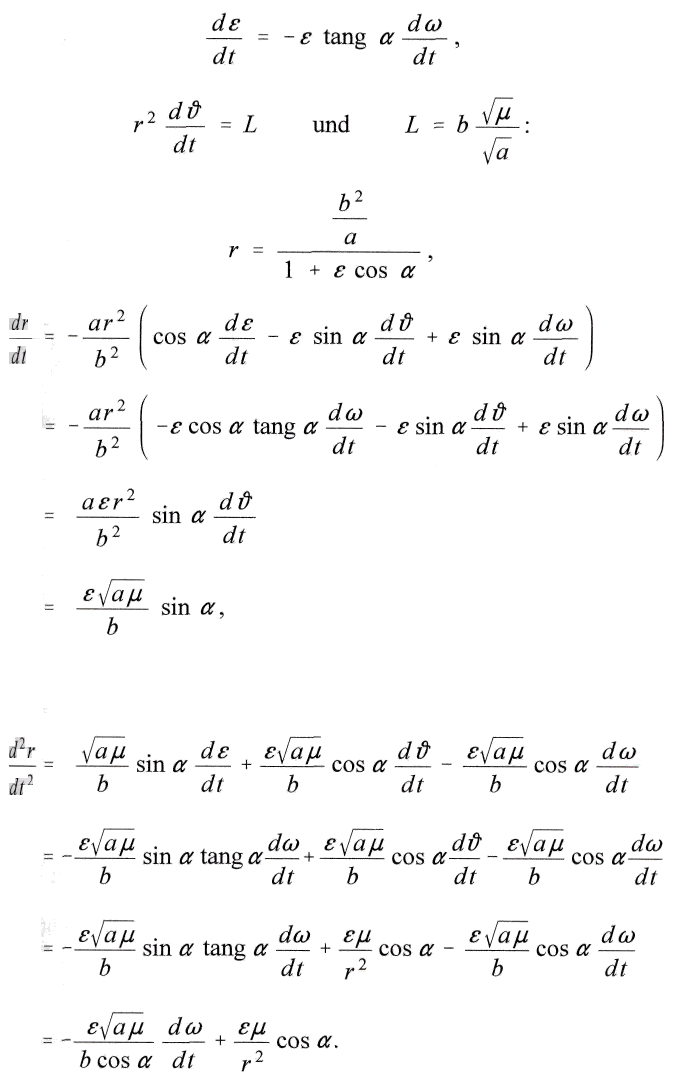
Также
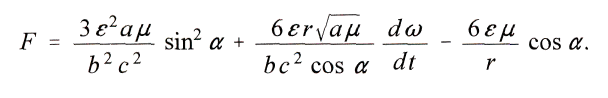
Поэтому искомое выражение для уравнения
dω/dt будет таким: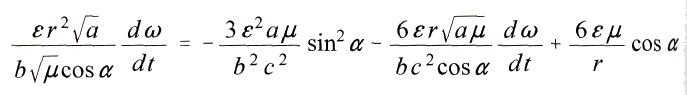
или, использовав то, что

и разделив на
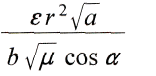
получим
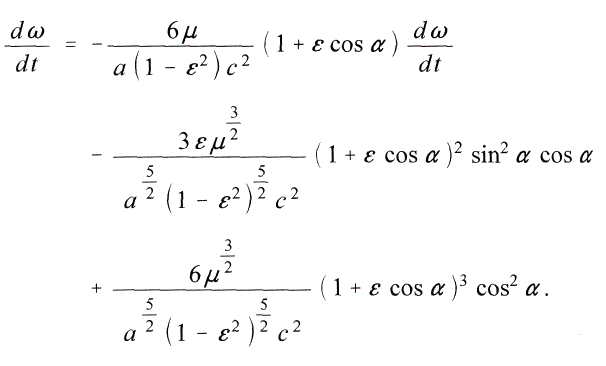
При сравнивании с наблюдениями вычисленного таким образом выражения для
dω/dt надо учесть, что решение относится только к одной единственной планете. Поэтому можно рассматривать только движения перигелия, возникающие не из возмущений. Таковые известны только у Меркурия, равные величине 41΄΄ ηа столетие. Эта незначительная величина заранее исключает любое опытное подтверждение постоянной изменчивости dω/dt. Следовательно, надо брать интеграл за длительное время. В последнем уравнении имеется ε, но нет dε/dt; и так как изменения ε по сравнению с ε исчезающе малы, то его можно считать константой.Следовательно, достаточно выбрать пределами интегрирования α = 0 и α
= π/2, ςак как dω/dt при каждом последующем обороте вокруг Солнца повторяет те же значения с большим приближением.Уравнение для
dω/dt надо умножить на dt и вставить во второй и третий член справа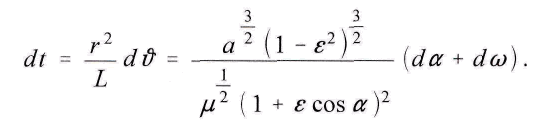
После преобразования и деления получим
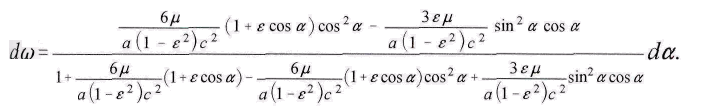
Разделив числитель и знаменатель на
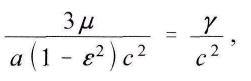
упорядочив выражение по возрастающим степеням
cos α заменив для краткости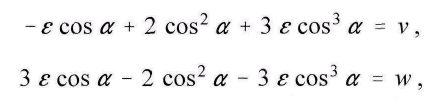
получим
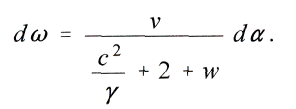
Приближённо можно получить
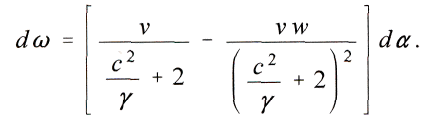
Для движения ψ перигелия за один оборот получим
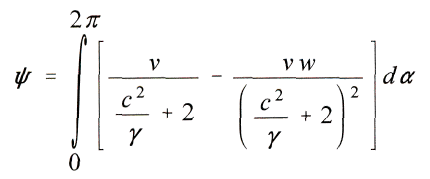
или, так как
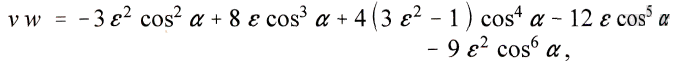
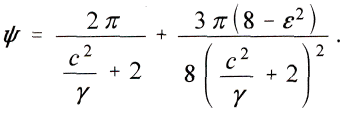
из этого следует
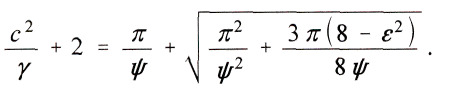
Учитывая, что ψ очень мало, можно увидеть, что второй член исчезающе мал по сравнению с первым. Выбранное для
dω οриближённое выражение всё ещё слишком точное, т.е. величиной w можно было бы с самого начала пренебречь. Таким образом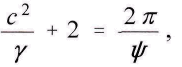
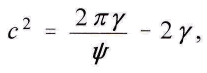
по той же причине величиной 2γ можно пренебречь по сравнению с 2π
γ/ ψ. Ο поэтомуЗаключительно мы получим
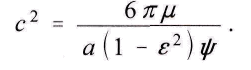
Здесь
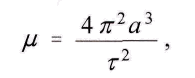
где τ - период обращения планеты.
Для Меркурия мы получим следующие величины
a
= 0,3871·149·106 kmε
= 0,2056τ
= 88 сутокψ
= 4,789·10-7Этим самым мы находим
c
= 305 500 km/sec.
Наименьшую величину скорости света до сих пор нашёл Фуко
c = 298000 км/сек; наибольшая получена по последним наблюдениям по методу Рёмера c = 308000 км/сек; скорость 320 000 км/сек нашёл в своих экспериментах Герц для электрических волн.Следовательно, скорость распространения гравитационного потенциала совпадает со скоростью света и со скоростью электрических волн.
В этом одновременно состоит доказательство того, что эта скорость существует. Конечно, никто не будет отрицать, что движение перигелия Меркурия на угол 41΄
΄ ηа столетие может зависеть от других нам ещё незнакомых обстоятельств, и потому обязательной необходимости в конечной скорости распространения гравитационного потенциала нет.Следует, впрочем, учесть, что определяющая формула для зависимости потенциала от подобной скорости, в отличие от всех прежних результатов подобных исследований, найдена здесь совершенно естественным путём, не ведущим через сложные гипотезы.
Было бы удивительным совпадением, если бы посредством этих 41 секунд Меркурия можно было бы найти скорость света и электричества, без того, чтобы они имели какое-либо отношение к пространственно-временному распространению гравитации, в то время как среда, в которой имеет место это распространение, и движение света, и электрических волн, является тем самым пространством, расположенным между этими космическими телами. Даже относительно большая скорость движения перигелия, которую можно найти с помощью найденной величины
c для Венеры, а именно 8΄΄ ηа столетие, не может служить обоснованным аргументом. Для того, чтобы ревизия возмущений этой планеты была бы окончательной, надо исключить возможность случайности этого числа. Следует напомнить, что вычисления секулярного ускорения Луны может колебаться между 6΄΄ θ 12΄΄. Β остальном наблюдаются только незначительные движения перигелия.По легко находимым в обычно применяемых таблицах результатам наблюдений движения перигелия составляют за одно столетие для Земли 3΄
΄,6, δля Луны 0΄΄,06, δля Марса 1΄΄,3, δля Юпитера 0΄΄,06, δля Сатурна 0΄΄, 01, δля Урана 0΄΄,002, δля Нептуна 0΄΄, 0007.